更新:2024/10/22
【物理】a-tグラフ(加速度-時間グラフ)の意味と面積について
グラフ.png.webp)
はるか
a-tグラフ…加速度が時間とどう関係しているかを示す。
ふゅか
そうそう!縦軸に加速度、横軸に時間をとって、運動の変化を見やすくするグラフだよ!
1. a-tグラフ
a-tグラフとは、加速度 (a) を縦軸に、時間 (t) を横軸にとったグラフのことです。物体が運動している際、加速度がどのように変化しているのかを視覚的に示すものです。
- 加速度 (a): 速度の変化率を表し、単位時間あたりの速度の変化を示します。単位は \( \text{m/s}^2 \) です。
- 時間 (t): 運動が行われる時間の経過を示します。
2. a-tグラフからわかること
はるか
加速度がゼロの場合。等速運動か静止中だよね。
ふゅか
うん、グラフが横軸に沿った水平線になるんだよ!何も加速してないから、ずーっと同じ速さで動いてるか、止まってるってことだね!
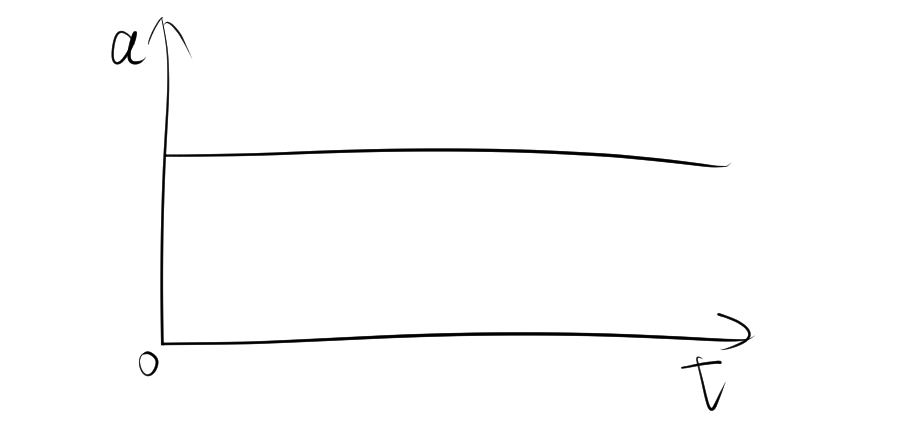
2.1. 加速度が一定の場合
グラフ上では、水平な直線で表されます。これは、加速度が変化せず一定であることを意味します。たとえば、物体が自由落下している場合、重力加速度は約 \( 9.8 \, \text{m/s}^2 \) で一定です。
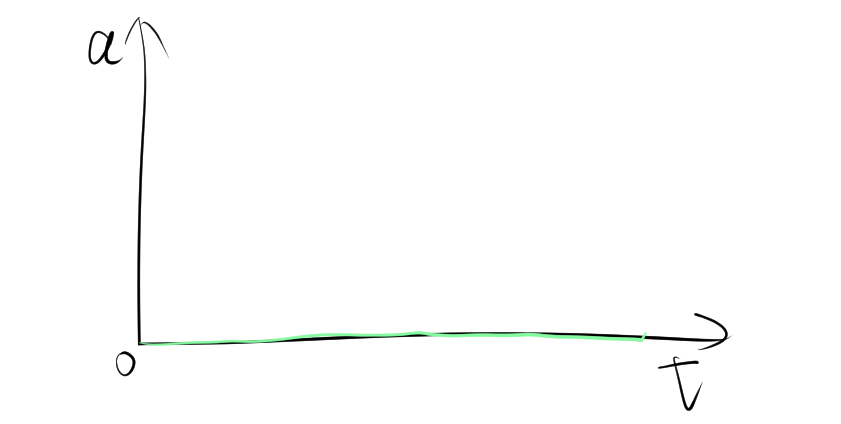
2.2. 加速度がゼロの場合
加速度がゼロのとき、a-tグラフは横軸(加速度が 0 の線)上に沿った水平線となります。これは、物体が等速運動をしているか、静止していることを示します。
3. a-tグラフから速度を求める
a-tグラフの面積を計算することで、速度の変化を得ることができます。
微分から、加速度 \(a\) は速度の時間に対する変化率、つまり
\[ a = \frac{dv}{dt} \]
と表されます。これを積分すると、速度を得ることができます。
時間 \(t_1\) から \(t_2\) までの間の加速度 \(a\) を時間で積分することで、速度の変化 \(\Delta v\) が求められます
\[ \Delta v = \int_{t_1}^{t_2} a(t) \, dt \]
つまり、a-tグラフの下の面積が速度の変化を表します。たとえば、加速度が一定の場合、加速度が長く続くほど速度が大きく変化することを表しており、その面積が速度の増加に対応します。
直感的には、a-tグラフの面積は、加速度(時間あたりの速度変化)がどれくらい続いたかを表しているので、その面積が大きいほど速度が大きく変化する、ということが感覚的に理解できます。
4. 関連した記事
PR