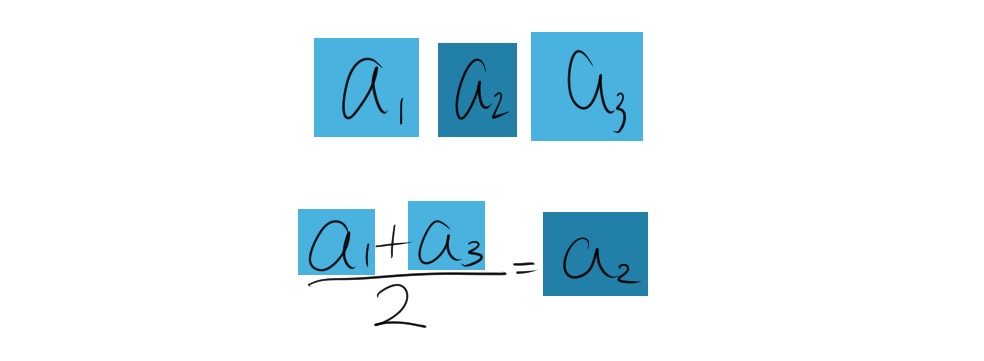等差数列とは?例題や性質、漸化式、グラフについて

1. 等差数列とは
等差数列とは、隣り合う項同士の差が常に一定である数列のことを指します。この一定の差を「公差」と呼びます。
\[ a_n = a + (n – 1) d \]
例えば、初項が 3 で公差が 2 の等差数列は次のようになります。
\[ 3, 5, 7, 9, 11, \dots \]
この場合、各項の間の差(公差)は 2 です。
1.1. 等差数列の漸化式
等差数列の漸化式は、各項がその直前の項に一定の値(公差)を加えることで表されます。
例えば、初項が \( a_1 = 3 \) で、公差が \( d = 2 \) の場合、漸化式は次のようになります。
\[ a_{n+1} = a_n + 2 \]
これにより、数列の各項は以下のように計算されます。
- \( a_1 = 3 \)
- \( a_2 = a_1 + 2 = 3 + 2 = 5 \)
- \( a_3 = a_2 + 2 = 5 + 2 = 7 \)
- \( a_4 = a_3 + 2 = 7 + 2 = 9 \)
2. 等差数列
2.1. 2項の和
等差数列の一般項の式を使って、項 \( a_{n-k} \) と \( a_{n+k} \) を表します。
\[ a_{n-k} = a_1 + (n-k-1) d \]
\[ a_{n+k} = a_1 + (n+k-1) d \]
次に、これら2つの項の和の平均を計算します。
\[\begin{align*} \frac{a_{n-k} + a_{n+k}}{2} &= \frac{\left( a_1 + (n-k-1) d \right) + \left( a_1 + (n+k-1) d \right)}{2} \\ &= \frac{2a_1 + (n-k-1)d + (n+k-1)d}{2} \\ &= \frac{2a_1 + (n-1)d + (n-1)d}{2} \\ &= \frac{2a_1 + 2(n-1)d}{2} \\ &= a_1 + (n-1)d \\ &=a_n \end{align*}\]
イメージ図は次のようになります。
2.2. 数列の和
\[\begin{align*} S_n &= \frac{n}{2} (a_1 + a_n) \\ &=\frac{n}{2} (2a_1 + (n – 1) d) \end{align*}\]
和の公式の導出は次のページで行っています。
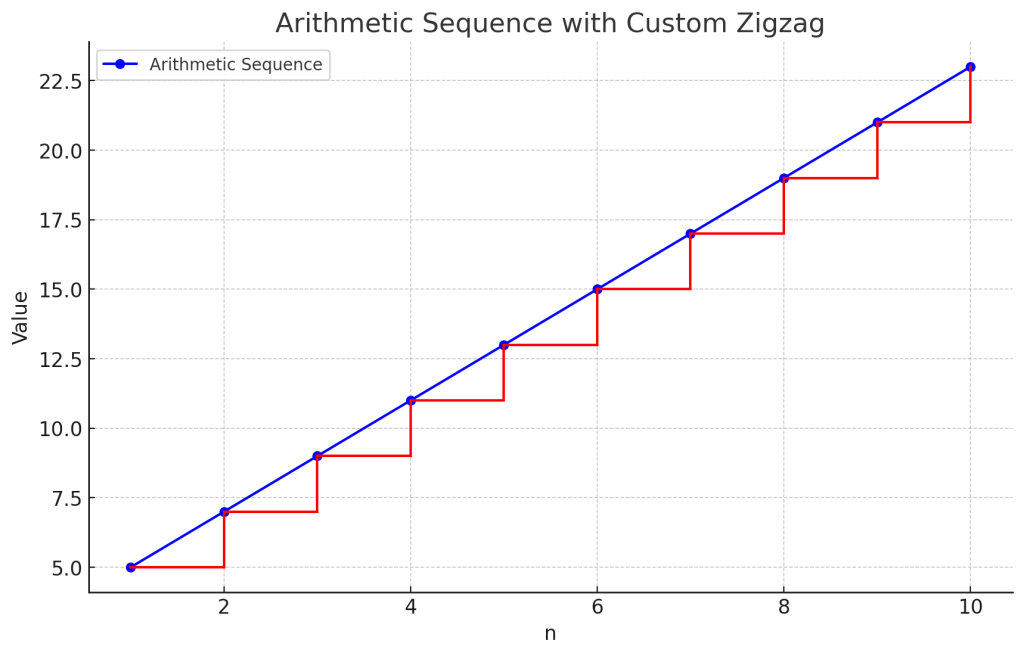
2.3. グラフは直線
等差数列の各項をプロットすると、各点が直線上に並びます。等差数列は一次関数に対応するグラフを持っています。直線の傾きが公差 \( d \) であり、初項 \( a_1 \) は \( n = 1 \) のときの切片です。
2.4. 総乗
\[ P_n = d^{n+1} \cdot \frac{\Gamma \left( \frac{a_0}{d} + n + 1 \right)}{\Gamma \left( \frac{a_0}{d} \right)} \]
3. 等差数列の例題
3.1. 例題1: 初項と公差を求める
第3項と第7項について、以下の連立方程式が立てられます。
$$a_3 = a_1 + 2d = 8 $$
$$ a_7 = a_1 + 6d = 20 $$
この連立方程式を解くと、初項 \(a_1 = 2\) と公差 \(d = 3\) が求められます。
3.2. 例題2: 第n項を求める
初項 \(a_1 = 4\)、公差 \(d = 5\)、\(n = 12\) であるから、
\[ a_{12} = 4 + (12-1) \times 5 = 4 + 55 = 59 \]
第12項は59です。
3.3. 例題3: 合計を求める
まず第20項 \(a_{20}\) を求めます。
\[ a_{20} = 2 + (20-1) \times 3 = 2 + 57 = 59 \]
和を求めると、
\[ S_{20} = \frac{20}{2}(2 + 59) = 10 \times 61 = 610 \]
この等差数列の和は610です。