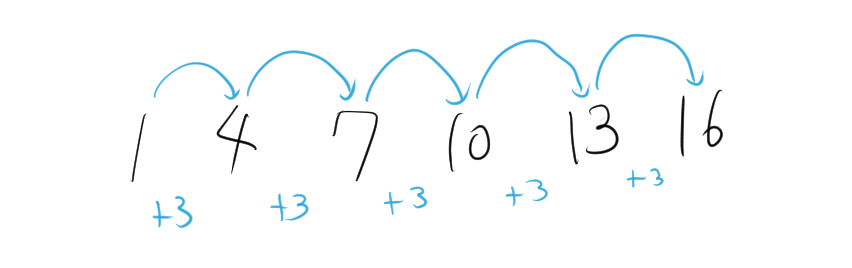
等差数列の和の公式の2通りの証明と具体例について

1. 等差数列とは？

等差数列とは、隣り合う項の差が常に一定である数列のことです。この差を公差と呼びます。一般に、等差数列の初項を \( a_1 \)、公差を \( d \)、第 \( n \) 項を \( a_n \) とすると、等差数列は以下のように表されます。

\[ a_1, a_1 + d, a_1 + 2d, \dots, a_1 + (n-1)d \]

2. 等差数列の和の公式

2.1. 具体例

例えば、初項 \( a_1 = 3 \)、公差 \( d = 2 \)、項数 \( n = 5 \) の等差数列の和を求めてみましょう。

各項は次のようになります。

\[ 3, 5, 7, 9, 11 \]

第 5 項は \( a_n = 3 + (5-1) \times 2 = 11 \) です。

等差数列の和は、次の公式を使って求めます。

\[ S_5 = \frac{5}{2} \times (3 + 11) = \frac{5}{2} \times 14 = 35 \]

したがって、和は 35 です。

このようにして、等差数列の和を簡単に計算することができます。

3. 証明

3.1. 等差数列の和の導出

等差数列の和 \( S_n \) は、次のように書けます。

\[ S_n = a_1 + (a_1 + d) + (a_1 + 2d) + \dots + (a_1 + (n-1)d) \]

逆に、$a_n$から公差 \( d \)を引いていくと

\[ S_n =a_n + (a_n -d) + (a_n -2d) \dots + a_n- (n-1)d \]

この2つの式を足し合わせると、各項が同じ値になります。

\[ 2S_n = (a_1 + a_n) + (a_1 + a_n) + \dots + (a_1 + a_n) \]

項数が \( n \) あるので、これをまとめると

\[ 2S_n = n  (a_1 + a_n) \]

両辺を 2 で割ると、最終的に等差数列の和の公式が得られます。

\[ S_n = \frac{n}{2} (a_1 + a_n) \]

$a_n=a_1+(n-1)d$より、

\[\begin{align*} S_n = \frac{n}{2} (a_1 + a_1+(n-1)d) \\ &=\frac{n}{2} \{2a_1 +(n-1)d\} \end{align*}\]

3.2. 数学的帰納法を利用した証明

この公式を数学的帰納法を使って証明してみましょう。

---

まず、\( n = 1 \) の場合の和 \( S_1 \) を確認します。この場合、数列の最初の項だけを考えます。

\[ S_1 = a_1 \]

公式に \( n = 1 \) を代入して確認します。

\[ S_1 = \dfrac{1}{2} (a_1 + a_1) = a_1 \]

$n=1$で成り立つことが確認できました。

次に、\( n = k \) の場合に公式が成り立つと仮定します。つまり、次を仮定します。

\[ S_k = \dfrac{k}{2} (a_1 + a_k) \]

\( n = k + 1 \) の場合の和 \( S_{k+1} \) は、\( S_k \) に第 \( k+1 \) 項 \( a_{k+1} \) を加えたものであるので、

\[ S_{k+1} = S_k + a_{k+1} \]

ここで、$a_{k+1}$は

\[ a_{k+1} = a_1 + k d \]

仮定より \( S_k = \dfrac{k}{2} (a_1 + a_k) \) なので、

\[ S_{k+1} = \dfrac{k}{2} (a_1 + a_k) + (a_1 + k d) \]

次に、\( a_k = a_1 + (k-1)d \) を使い、整理します。

\[ \begin{align*} S_{k+1} &= \dfrac{k}{2} (a_1 + a_1 + (k-1)d) + (a_1 + k d)\\ &= \dfrac{k}{2} (2a_1 + (k-1)d) + (a_1 + k d) \\ &=ka_1 +\frac{k}{2}(k-1)d +a_1 + k d \\ &=(k+1)a_1+kd\left(\frac{1}{2}(k-1)+1\right) \\ &=(k+1)a_1+\frac{1}{2}(k+1)kd \\ &=(k+1)\left(a_1+\frac{1}{2}kd \right) \\ &=\frac{(k+1)\left(2a_1+kd \right)}{2} \\ &=\frac{(k+1)\left(a_1+a_1+kd \right)}{2} \\ &=\frac{(k+1)\left(a_1+a_{k+1}\right)}{2} \\ \end{align*} \]

よって、\( n = k + 1 \) の場合も公式が成り立つことが証明されました。

数学的帰納法により、等差数列の最初の \( n \) 項の和 \( S_n \) は、次の公式で表されることが証明されました。

\[ S_n = \dfrac{n}{2} (a_1 + a_n) \]