【Python】簡単に状態遷移図を作成することができる！automata-libの使い方について

1. automata-lib

今回はpythonのライブラリであるautomata-libの使い方について説明させていただきます。これが使えれば、答えのないオートマトンの問題（大学の教科書）の助けになります。

1.1. インストール方法

PyPIの場合:

pip install automata-lib

Githubの場合:

pip install git+https://github.com/caleb531/automata.git

PyPIからインストールしたときに、正規表現がうまく動かなかったため、私はgithubからインストールしました。また、オートマトンのグラフを表示したい場合は、graphvizをインストールする必要があります。

1.2. 決定性有限オートマトン(DFA)

from automata.fa.dfa import DFA

まず、automata.fa.dfaからDFAをimportする必要があります。これで、DFAを作ることができるようになりました。

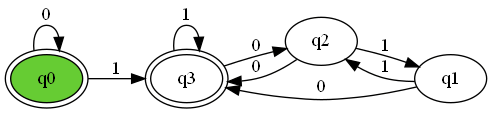
そして、以上の画像のオートマトンは以下のように書くとDFAを作ることができます。

dfa = DFA(
    states={'q0', 'q1', 'q2','q3'},
    input_symbols={'0', '1'},
    transitions={
        'q0': {'0': 'q0', '1': 'q3'},
        'q1': {'0': 'q3', '1': 'q2'},
        'q2': {'0': 'q3', '1': 'q1'},
        'q3': {'0': 'q2', '1': 'q3'},
        
    },
    initial_state='q0',
    final_states={'q0','q3'}
)

DFAの中に、states、input_symbols、transitions、initial_state、final_statesを辞書型で書くことでオートマトンを定義することができる。

1.3. DFAの引数の意味

states・・・状態を書く。上の場合はq0、q1、q2、q3が状態です。
input_symbols・・・DFAの入力を書きます。
transitions・・・状態遷移を書きます。例えば、上記のDFAの場合、’q0’は’0’のとき、’q0’に移動して、’1’のとき、’q3’に移動します。
initial_state・・・DFAの初期状態を書きます。
final_states・・・DFAの受理状態を書きます。

1.4. DFA.read_input

dfa.read_input('111') #'q3'
dfa.read_input('1101') #RejectionException

read_inputでは言語が受理するかどうかを判定することができます。
受理するときは、受理状態が返されて、受理しないときはRejectionExceptionとなり、エラーとなります。

1.5. DFA.accepts_input

dfa.accepts_input('111') #True
dfa.accepts_input('1101') #False

accepts_inputは言語を受理するかどうかをTrue、Falseで返してくれます。受理する場合はTrue、受理しない場合は、Falseです。

1.6. 最小化

MinDfa=dfa.minify()

minifyを用いることで、最小化することができます。
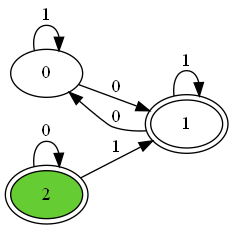
MinDfaは以下のようになります。

2. オートマトンの表示

dfa.show_diagram("dfa.png")

show_diagram()にファイル名・保存先を書くことで、オートマトンの状態遷移図の画像を作ることができます。緑色で塗られた部分が初期状態で、二重に線がひかれている部分が受理状態です。しかし、Graphvizをインストールする必要があります。

2.1. 非決定性有限オートマトン(NFA)

from automata.fa.nfa import NFA

まず、automata.fa.nfaからNFAをimportします。これでNFAを作ることができるようになりました。

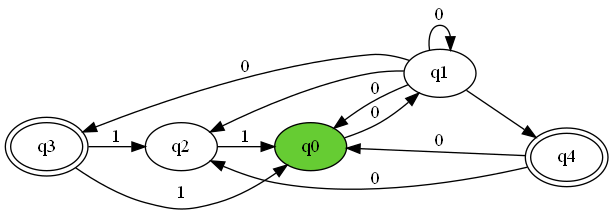
DFAと基本的に同様に考えてコードを書けば問題ありません。ただし、状態遷移のvalue(例えば、’q4’の’0’のときのvalueは{‘q0′,’q2’})はsetで書きます。

nfa = NFA(
    states={'q0', 'q1', 'q2','q3','q4'},
    input_symbols={'0', '1'},
    transitions={
        'q0': {'0': {'q1'}},
        'q1': {'0': {'q1','q3','q0'}, '': {'q2','q4'}},
        'q2': {'1': {'q0'}},
        'q3': {'1': {'q2','q0'}},
        'q4':{'0':{'q0','q2'}}
    },
    initial_state='q0',
    final_states={'q3','q4'}
)

2.2. NFA.read_input

nfa.read_input('0') #frozenset({'q1', 'q2', 'q4'})
nfa.read_input('111') #RejectionException

read_inputでは同様に言語が受理するかどうかを判定することができます。
受理するときは、停止する状態が返されて、受理しないときはRejectionExceptionとなり、エラーとなります。

2.3. NFA.accepts_input

nfa.accepts_input('0') #True
nfa.accepts_input('111') #False

accepts_inputは同様に言語を受理するかどうかをTrue、Falseで返してくれます。受理する場合はTrue、受理しない場合は、Falseです。

3. 正規表現

$(aab+bba)^*$という正規表現を考えると以下のように表現することができます。

(aab|bba)*

と書きます。
+は|と書くので注意しましょう。

4. オートマトンの変換

4.1. NFAからDFA

from automata.fa.dfa import DFA
from automata.fa.nfa import NFA

DFAとNFAをimportする必要があります。
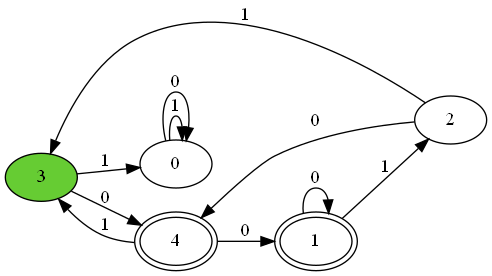
DFA.from_nfa(対象のnfa)を用いることで、DFAに変換することができます。また、NFAが変換されると、最小のDFAが生成されます。

dfa = DFA.from_nfa(nfa)

試しに、先ほど紹介したNFAをDFAに変換すると以下のようになります。

4.2. 正規表現からNFA・DFA

nfa = NFA.from_regex('(aab|bba)*', input_symbols={'a', 'b'})
dfa=DFA.from_nfa(nfa)

正規表現からNFAにNFA.from_regexを用いることで変換します。入力はinput_symbolsに定義します。上の場合はa、bが入力です。
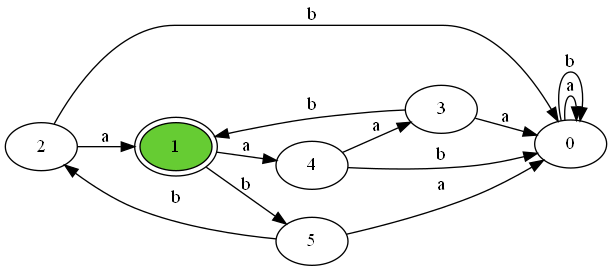
そして、DFA.from_nfaを用いて、NFAからDFAに変換すると、正規表現からDFAを生成することができます。
上記のDFAは以下のようになります。

---

Pythonの記事のまとめ