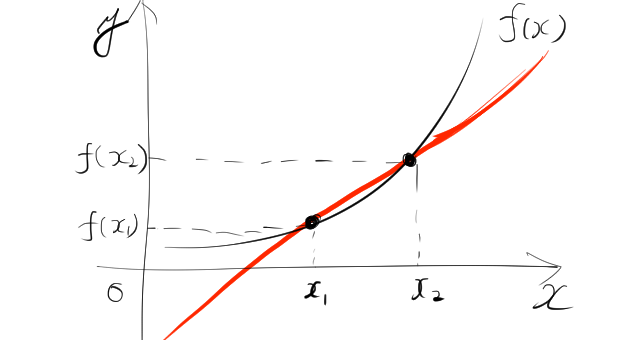
平均変化率の定義・例題について

はるか

平均変化率って、何か分かる？

ふゅか

うん、もちろん！関数の2点間でどれだけ変化したかを示す指標よね。例えば、グラフ上で2点を結ぶ直線の傾きにあたるの。

1. 平均変化率とは

これは、関数 \( f(x) \) のグラフ上の \( (x_1, f(x_1)) \) と \( (x_2, f(x_2)) \) という2つの点を結んだ直線の傾きに対応します。直線の傾きは、2点間での \(x\) の変化に対する \( f(x) \) の変化の割合を示しており、この傾きが平均変化率です。

2. 練習問題

ふゅか

実際に平均変化率を計算してみよう！

2.1. 練習問題 1:二次関数

関数 \( f(x) = 3x^2 + 2x + 1 \) の \( x_1 = 1 \) から \( x_2 = 4 \) の区間における平均変化率を求めます。

まず、各点での関数の値を計算します。

• \( f(1) = 3(1)^2 + 2(1) + 1 = 3 + 2 + 1 = 6 \)
• \( f(4) = 3(4)^2 + 2(4) + 1 = 3(16) + 8 + 1 = 48 + 8 + 1 = 57 \)

次に、平均変化率を計算します。

\[ \frac{f(4) – f(1)}{4 – 1} = \frac{57 – 6}{3} = \frac{51}{3} = 17 \]

したがって、平均変化率は 17 です。

2.2. 練習問題 2:三角関数

関数 \( f(x) = \sin x \) の \( x_1 = 0 \) から \( x_2 = \frac{\pi}{2} \) の区間における平均変化率を求めます。

まず、各点での関数の値を計算します。

• \( f(0) = \sin(0) = 0 \)
• \( f\left(\frac{\pi}{2}\right) = \sin\left(\frac{\pi}{2}\right) = 1 \)

次に、平均変化率を計算します。

\[ \frac{f\left(\frac{\pi}{2}\right) – f(0)}{\frac{\pi}{2} – 0} = \frac{1 – 0}{\frac{\pi}{2}} = \frac{1}{\frac{\pi}{2}} = \frac{2}{\pi} \]

したがって、平均変化率は \(\dfrac{2}{\pi}\)です。

2.3. 練習問題 3:指数関数

関数 \( f(x) = e^x \) の \( x_1 = 1 \) から \( x_2 = 3 \) の区間における平均変化率を求めます。

まず、各点での関数の値を計算します。

• \( f(1) = e^1 = e \)
• \( f(3) = e^3 \)

次に、平均変化率を計算します。

\[ \frac{f(3) – f(1)}{3 – 1} = \frac{e^3 – e}{2} = \frac{e(e^2 – 1)}{2} \]

したがって、平均変化率は \(\dfrac{e(e^2 – 1)}{2}\)です。