2値エントロピー関数の性質・グラフについて

ふゅか

今日は二値エントロピー関数について話すの？二値エントロピーって、ちょっと難しそうだけど、面白そう！

はるか

二値エントロピー関数は、確率変数が2つの離散値を取る場合のエントロピーを計算するためのもの。例えば、成功と失敗の確率を考えるとわかりやすい。

1. 二値エントロピー関数

二値エントロピー関数は、確率変数が2つのカテゴリ（例えば、成功と失敗、1と0など）のいずれかを取る場合のエントロピーを計算するための関数です。

この関数の意味を詳しく説明します。

2. 関数の性質

ふゅか

確率 \( p \) が0か1に近いときにはエントロピーが0になるんだよね。最大になるのはどこなの？

はるか

最大になるのは \( p = 0.5 \) のとき。確率がちょうど半々のとき、情報の不確実性が最大になるからエントロピーも最大値を取る。

2.1. p=0またはp=1のとき

$p=0$または$p=1$のとき、$0\log_2 0$となっていまいますが、

\[ \lim_{x \to +0} x \log x=0 \]

となるので、$f(0)=f(1)=0$とします。極限についてはxlogxにて解説しいます。

2.2. 関数の微分

二値エントロピー関数 \( H(p) = -p \log_2(p) – (1 – p) \log_2(1 – p) \) の微分を求めてみましょう。まず、この関数を微分する際に便利な対数の性質を使用します。自然対数を使うために、 \(\log_2(x) = \frac{\ln(x)}{\ln(2)}\) を利用します。

\[ H(p) = -p \frac{\ln(p)}{\ln(2)} – (1 – p) \frac{\ln(1 – p)}{\ln(2)} \]

ここで微分を行います。 \(H(p)\) の微分を \(H'(p)\) として表します。

\[ H'(p) = -\frac{1}{\ln(2)} \left( \ln(p) + p \cdot \frac{1}{p} \right) + \frac{1}{\ln(2)} \left( \ln(1 – p) + (1 – p) \cdot \left(-\frac{1}{1 – p}\right) \right) \]

これらを組み合わせると、

\[ H'(p) = -\frac{1}{\ln(2)} \ln(p) – \frac{1}{\ln(2)} + \frac{1}{\ln(2)} \ln(1 – p) – \frac{1}{\ln(2)} \]

整理すると、

\[ H'(p) = \frac{1}{\ln(2)} \left( \ln(1 – p) – \ln(p) \right) \]

\[ H'(p) = \frac{1}{\ln(2)} \ln\left(\frac{1 – p}{p}\right) \]

\[ H'(p) = \frac{1}{\ln(2)} \log_2\left(\frac{1 – p}{p}\right) \]

したがって、二値エントロピー関数の微分は次のようになります。

\[ H'(p) = \log_2\left(\frac{1 – p}{p}\right) \]

これはロジット関数です。

はるか

微分の結果は最終的にロジット関数と同じ形。

2.3. 関数の最大値

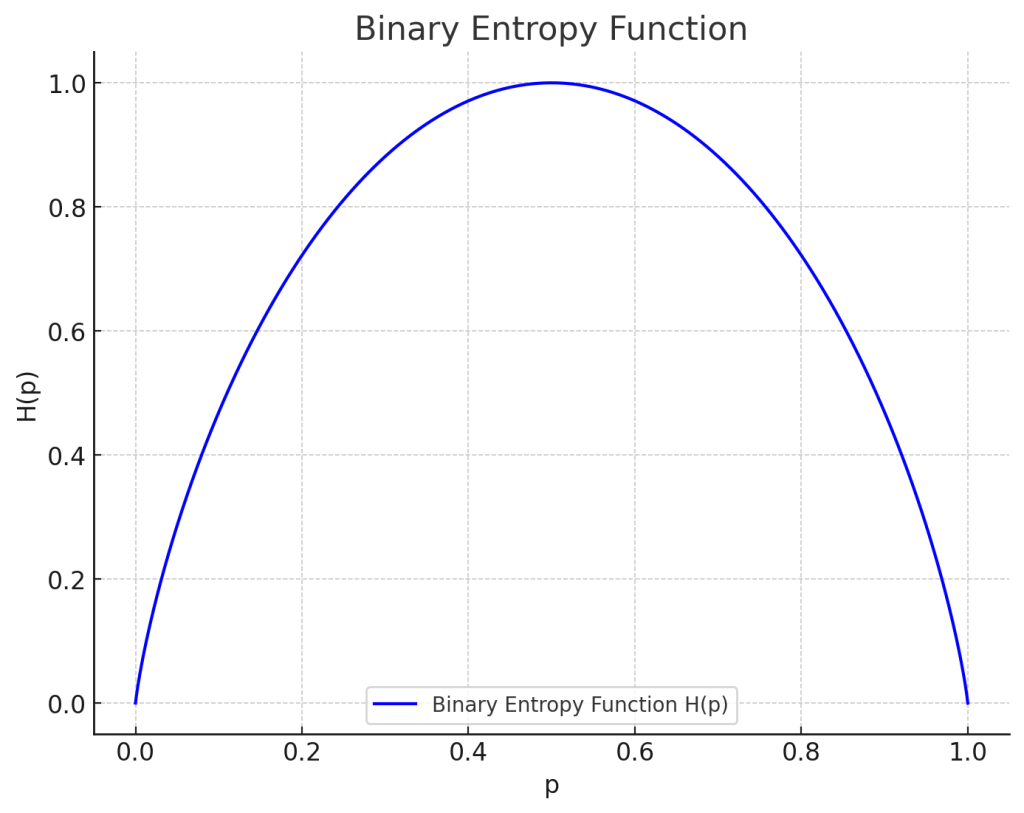
エントロピーが最大になるのは、確率 \(p = 0.5\) のときです。このとき、 \(X\) が 0 または 1 になる確率が同じなので、最も不確実であり、情報量が最大となります。この最大エントロピーの値は \(H(0.5) = 1\) です。

3. グラフ

3.1. 関数の極値

\[ H'(p) = \log_2\left(\frac{1 – p}{p}\right) \]

極値を求めるためには、この微分が 0 になる点を探します。

\[ \log_2\left(\frac{1 – p}{p}\right) = 0 \]

この方程式を解くと、

\[ \frac{1 – p}{p} = 1 \]

これをさらに整理すると、

\[ 1 – p = p \]

\[ 1 = 2p \]

\[ p = \frac{1}{2} \]

したがって、二値エントロピー関数 \( H(p) \) は \( p = \frac{1}{2} \) で極値を持ちます。

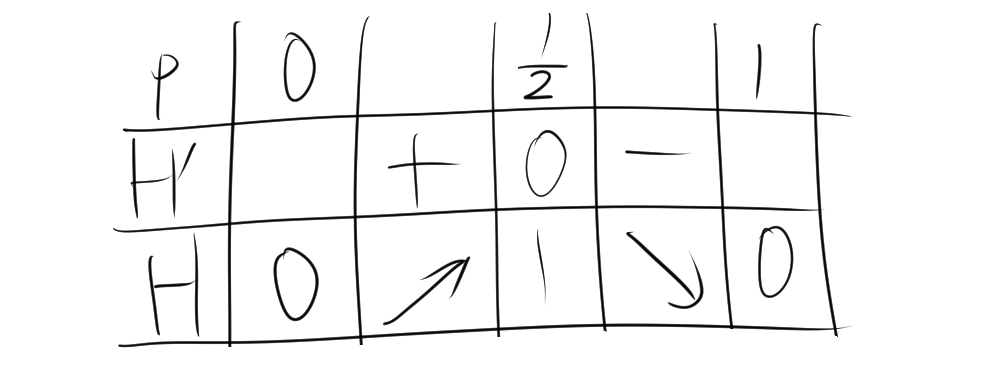
増減表を書くと次のようになります。

\( p = \frac{1}{2} \) は最大値となります。

3.2. グラフを書く

2値エントロピー関数のグラフを書くと次のようになります。