【図解】二項定理の二つの証明、具体例、例題について

1. 二項定理とは

ここで、

• \({}_n \mathrm{C}_k\) は 二項係数 と呼ばれ、次のように計算されます。 \[ {}_n \mathrm{C}_k = \frac{n!}{k!(n-k)!} \]
• \(a^{n-k}\) と \(b^k\) はそれぞれ、\(a\) と \(b\) のべき乗です。
• 二項定理は二項展開とも呼ばれます。

1.1. 具体例

例えば、\((a + b)^3\) を展開してみましょう。

\[ (a + b)^3 = {}_3 \mathrm{C}_0 a^3 + {}_3 \mathrm{C}_1 a^2b + {}_3 \mathrm{C}_2 ab^2 + {}_3 \mathrm{C}_3 b^3 \]

それぞれの項を計算すると

\[ = 1 \cdot a^3 + 3 \cdot a^2b + 3 \cdot ab^2 + 1 \cdot b^3 \]

したがって、\((a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3\) となります。

1.2. パスカルの三角形

二項係数は、パスカルの三角形と呼ばれる図形に対応しています。この三角形の各行には、二項展開における係数が並んでいます。例えば、次のように構成されます。

\[ \begin{array}{ccccccc} & & & 1 & & & \\ & & 1 & & 1 & & \\ & 1 & & 2 & & 1 & \\ 1 & & 3 & & 3 & & 1 \\ \end{array} \]

上から4行目が、\((a + b)^3\) の展開の係数 \(1, 3, 3, 1\) を表しています。

2. 二項定理の証明

2.1. 数学的帰納法による証明

数学的帰納法を利用して証明します。

まず、\( n = 1 \) の場合を確認します。

左辺は

\[ (a + b)^1 = a + b \]

右辺は

\[ \sum_{k=0}^{1} {}_1 \mathrm{C}_k a^{1-k} b^k = {}_1 \mathrm{C}_0 a^1 b^0 + {}_1 \mathrm{C}_1 a^0 b^1 = a + b \]

両辺が一致しているため、\( n = 1 \) では成り立ちます。

$n=k$のとき、

\[ (a + b)^k = \sum_{i=0}^{k} {}_k \mathrm{C}_i a^{k-i} b^i \]

が成り立つと仮定します。

次に、\( n=k+1 \) の場合の式を確認します。

左辺は次のように展開できます。

\[ (a + b)^{k+1} = (a + b) \cdot (a + b)^k \]

仮定を使用して、\( (a + b)^k \) を展開すると、

\[ \begin{align*}(a + b)^{k+1} &= (a + b) \cdot \left( \sum_{i=0}^{k} {}_k \mathrm{C}_i a^{k-i} b^i \right) \\ &= \sum_{i=0}^{k} {}_k \mathrm{C}_i a^{k+1-i} b^i + \sum_{i=0}^{k} {}_k \mathrm{C}_i a^{k-i} b^{i+1} \\ &= a^{k+1} + \sum_{i=1}^{k} {}_k \mathrm{C}_i a^{k+1-i} b^i + \sum_{i=0}^{k-1} {}_k \mathrm{C}_i a^{k-i} b^{i+1} + b^{k+1} \end{align*}\]

ここで、シグマの部分に着目して、$\displaystyle\sum_{i=0}^{k-1} {}_k \mathrm{C}_i a^{k-i} b^{i+1}$の添え字$i$をずらすと、

\[ \begin{align*} &\sum_{i=1}^{k} {}_k \mathrm{C}_i a^{k+1-i} b^i + \sum_{i=0}^{k-1} {}_k \mathrm{C}_i a^{k-i} b^{i+1} \\ &=\sum_{i=1}^{k} {}_k \mathrm{C}_i a^{k+1-i} b^i + \sum_{i=1}^{k} {}_k \mathrm{C}_{i-1} a^{k-(i-1)} b^{i-1+1} \\ &=\sum_{i=1}^{k} {}_k \mathrm{C}_i a^{k+1-i} b^i + \sum_{i=1}^{k} {}_k \mathrm{C}_{i-1} a^{k+1-i} b^{i} \\ &=\sum_{i=1}^{k}( {}_k \mathrm{C}_i +{}_k \mathrm{C}_{i-1})a^{k+1-i} b^i \end{align*}\]

ここで、パスカルの三角形の組み合わせの関係式\( {}_{k+1} \mathrm{C}_i = {}_k \mathrm{C}_i +{}_k \mathrm{C}_{i-1}\) を使用すると、

$$\sum_{i=1}^{k}( {}_k \mathrm{C}_i +{}_k \mathrm{C}_{i-1})a^{k+1-i} b^i   =\sum_{i=1}^{k} {}_{k+1} \mathrm{C}_i a^{k+1-i} b^i  $$

ここで、元の式に戻ると、

\[ \begin{align*}(a + b)^{k+1} &=a^{k+1} + \sum_{i=1}^{k} {}_k \mathrm{C}_i a^{k+1-i} b^i + \sum_{i=0}^{k-1} {}_k \mathrm{C}_i a^{k-i} b^{i+1} + b^{k+1} \\ &=a^{k+1} + \sum_{i=1}^{k} {}_{k+1} \mathrm{C}_i a^{k+1-i} b^i + b^{k+1} \\ &=\sum_{i=0}^{k+1} {}_{k+1} \mathrm{C}_i a^{k+1-i} b^i  \\ \end{align*}\]

これにより、\( n=k+1 \) の場合も成り立つことが示されました。

数学的帰納法により、全ての自然数 \( n \) に対して二項定理

\[ (a + b)^n = \sum_{k=0}^{n} {}_n \mathrm{C}_k a^{n-k} b^k \]

が成り立つことが証明されました。

2.2. 組み合わせを利用した証明

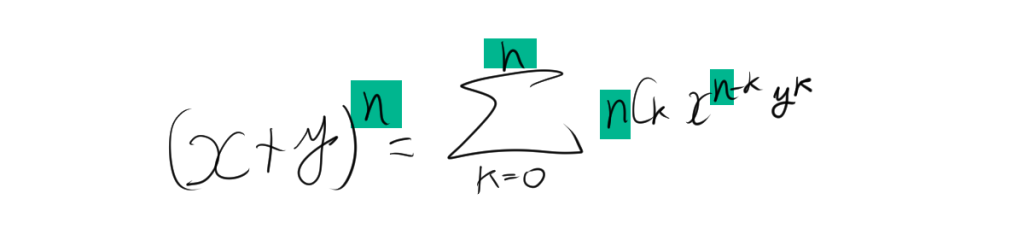
\( (x + y)^n \) を展開すると

\[ (x + y)^n = (x + y)(x + y) \cdots (x + y) \quad (n \text{ 回}) \]

この展開からそれぞれの項を計算する場合、それぞれの\((x + y)\) から \(x\) または \(y\) を選ぶ必要があります。すべての \(n\) 回の掛け算でどのように \(x\) と \(y\) を選ぶかがポイントです。

各掛け算で \(x\) または \(y\) のどちらかを選ぶため、合計 \(2^n\) 通りの選び方があります。その中で、\(k\) 個の \(y\) を選び、残りの \(n-k\) 個の \(x\) を選ぶ場合の数は組み合わせで計算することができます。\(n\) 回の選択の中で、ちょうど \(k\) 個の \(y\) を選ぶ方法の数は、\(y\)0 通りです。したがって、\(k\) 個の \(y\) を選んだ場合、項は次の形になります。

\[ {}_n\mathrm{C}_kx^{n-k} y^k \]

これを \(k = 0\) から \(n\) までの和として書くと、次の式が得られます。

\[ (x + y)^n = \sum_{k=0}^{n} {}_n\mathrm{C}_k \, x^{n-k} y^k \]

3. 二項定理の例題

3.1. 例題 1: 基本的な二項定理の展開

二項定理を使用すると、次のように展開できます。

\[ (x + 2)^4 = \sum_{k=0}^{4} {}_4 \mathrm{C}_k x^{4-k} 2^k \]

それぞれの項を計算していきます。

\[ = {}_4 \mathrm{C}_0 x^4 + {}_4 \mathrm{C}_1 x^3 \cdot 2 + {}_4 \mathrm{C}_2 x^2 \cdot 2^2 + {}_4 \mathrm{C}_3 x \cdot 2^3 + {}_4 \mathrm{C}_4 \cdot 2^4 \]

二項係数を計算します。

\[ (x + 2)^4 = 1 \cdot x^4 + 4 \cdot x^3 \cdot 2 + 6 \cdot x^2 \cdot 4 + 4 \cdot x \cdot 8 + 1 \cdot 16 \]

さらに計算すると、

\[ = x^4 + 8x^3 + 24x^2 + 32x + 16 \]

3.2. 例題 2: 負の数を含む二項定理の展開

二項定理を使用すると、次のように展開できます。

\[ (2a – 3)^3 = \sum_{k=0}^{3} {}_3 \mathrm{C}_k (2a)^{3-k} (-3)^k \]

それぞれの項を計算していきます

\[ = {}_3 \mathrm{C}_0 (2a)^3 + {}_3 \mathrm{C}_1 (2a)^2 (-3) + {}_3 \mathrm{C}_2 (2a)(-3)^2 + {}_3 \mathrm{C}_3 (-3)^3 \]

二項係数を計算します

\[ {}_3 \mathrm{C}_0 = 1,\quad {}_3 \mathrm{C}_1 = 3,\quad {}_3 \mathrm{C}_2 = 3,\quad {}_3 \mathrm{C}_3 = 1 \]

したがって、展開は次のようになります

\[ = 1 \cdot 8a^3 + 3 \cdot 4a^2 \cdot (-3) + 3 \cdot 2a \cdot 9 + 1 \cdot (-27) \]

さらに計算すると

\[ = 8a^3 – 36a^2 + 54a – 27 \]

3.3. 例題 3: 係数に分数を含む展開

二項定理を使用すると、次のように展開できます。

\[ \left(\frac{1}{2}x + \frac{3}{4}\right)^2 = \sum_{k=0}^{2} {}_2 \mathrm{C}_k \left(\frac{1}{2}x\right)^{2-k} \left(\frac{3}{4}\right)^k \]

それぞれの項を計算していきます

\[ = {}_2 \mathrm{C}_0 \left(\frac{1}{2}x\right)^2 + {}_2 \mathrm{C}_1 \left(\frac{1}{2}x\right) \cdot \frac{3}{4} + {}_2 \mathrm{C}_2 \cdot \left(\frac{3}{4}\right)^2 \]

二項係数を計算します

\[ {}_2 \mathrm{C}_0 = 1,\quad {}_2 \mathrm{C}_1 = 2,\quad {}_2 \mathrm{C}_2 = 1 \]

したがって、展開は次のようになります

\[ = 1 \cdot \frac{1}{4}x^2 + 2 \cdot \frac{1}{2}x \cdot \frac{3}{4} + 1 \cdot \frac{9}{16} \]

さらに計算すると

\[ = \frac{1}{4}x^2 + \frac{3}{4}x + \frac{9}{16} \]