ボルツァーノ=ワイエルシュトラスの定理の証明と具体例について

1. ボルツァーノ=ワイエルシュトラスの定理
1.1. 定理の要点
- 有界性: 数列 \((x_n)\) が有界であるとは、すべての \( n \) に対して \( |x_n| \leq M \) となるような定数 \( M > 0 \) が存在することを意味します。この場合、数列はある範囲内に収まります。
- 収束部分列: 数列の中から選んだ部分列が収束する。
1.2. 具体例
たとえば、数列 \(x_n= (-1)^n\) は、有界でありながら収束しません。しかし、ボルツァーノ=ワイエルシュトラスの定理によれば、この数列には収束部分列が存在するはずです。実際、この数列の部分列 \((-1, -1, -1, \ldots)\) は \(-1\) に収束し、部分列 \((1, 1, 1, \ldots)\) は \(1\) に収束します。
2. 証明
任意の有界数列が収束部分列を持つことを示すために、区間を二分していく方法(区間縮小法)を用います。この方法を使用して、数列の無限部分列がどの区間に無限に含まれるかを特定し、その中で収束部分列を構築します。
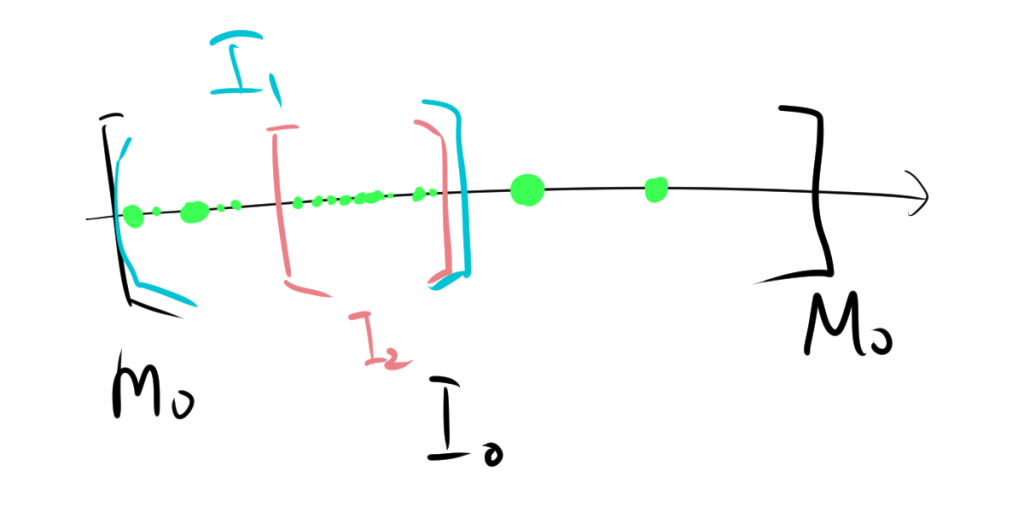
2.1. 区間縮小法
数列 \(\{a_n\}\) は有界であるため、上限 \(M_0\) と下限 \(m_0\) が存在します。つまり、すべての \(n\) に対して \(m_0 \leq a_n \leq M_0\) となります。このとき、初期区間を \(I_0 = [m_0, M_0]\) とします。
区間 \(I_0\) の中央を \(x_1 = \frac{M_0 + m_0}{2}\) として、区間を次の2つに分けます。
\[ [m_0, x_1] \quad \text{および} \quad [x_1, M_0] \]
そのような区間を \(I_1\) とし、端点を \(m_1\) および \(M_1\) とします。
この方法を帰納的に繰り返します。すなわち、区間 \(I_n = [m_n, M_n]\) が構築されていると仮定する。
$$x_{n+1} = \frac{M_n + m_n}{2}$$
とすると、次のようにして次の区間を構築します。
\[ I_{n+1} = \begin{cases} [m_n, x_{n+1}] & \text{もし } \{a_n\} \text{ の無限個の項がこの区間に含まれる場合} \\ [x_{n+1}, M_n] & \text{otherwise} \end{cases} \]
ここで、少なくとも一方の区間には \(\{a_n\}\) の元が無限個含まれます。
各区間の長さは次のように求められます。
\[ M_n – m_n = \frac{M_{n-1} – m_{n-1}}{2} = \frac{M_0 – m_0}{2^n} \]
したがって、\(n \to \infty\) のとき、 \[ \lim_{n \to \infty} (M_n – m_n) = \lim_{n \to \infty} \frac{M_0 – m_0}{2^n} = 0 \]
これは、区間の長さが 0 に収束することを示しています。
上記から、 \[ \lim_{n \to \infty} M_n = \lim_{n \to \infty} m_n = a \] となる共通の収束点 \(a\) が存在します。
数列 \(\{a_n\}\) の中で、各区間 \(I_i\) に属する元 \(a_{n_i}\) を選び出すことで部分列 \(\{a_{n_i}\}\) を構成します。各 \(i\) について、 \[ m_i < a_{n_i} < M_i \] であるため、はさみうちの原理から、 \[ \lim_{i \to \infty} a_{n_i} = a \] これにより、\(\{a_n\}\) の収束部分列が存在することが示されました。
この証明により、任意の有界な数列が収束部分列を持つことが示されました。