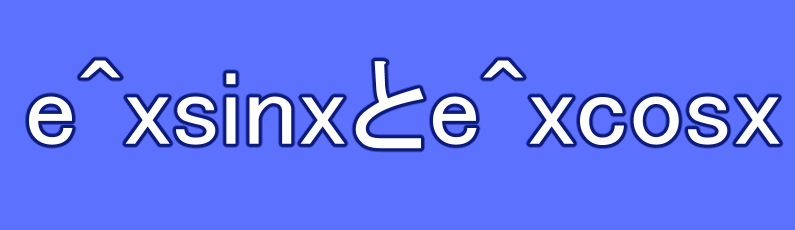数列と関数、集合の有界・上界・下界の定義・具体例・例題について

1. 有界な集合
1.1. 上界
$$x\leq K$$
上界の最小値を上限といいます。
1.2. 下界
$$x\geq k$$
下界の最大値を下限といいます。
1.3. 有界
$$k \leq x\leq K$$
2. 有界な集合の例題
2.1. 例題1
集合 \( A \) の要素は \( x < 5 \) なので、任意の \( x \geq 5 \) が上界になります。したがって、最小の上界(上限)は \( \sup A = 5 \) です。
集合 \( A \) の要素は \( x \geq 1 \) なので、任意の \( x \leq 1 \) が下界になります。したがって、最大の下界(下限)は \( \inf A = 1 \) です。
集合 \( A \) は上界と下界が存在するので、有界です。
2.2. 例題2
条件 \( x^2 < 4 \) から、\( -2 < x < 2 \) です。したがって、集合 \( B \) の上限は \( \sup B = 2 \) であり、下限は \( \inf B = -2 \) です。
集合 \( B \) は上界 と下界 が存在するので、有界です。
2.3. 例題3
自然数全体の集合であり、最大の数が存在しないため上界は存在しません。したがって、上限はありません。
一方、自然数の中で最小の数は \( 1 \) であり、これは下限です。したがって、集合 \( C \) の下限は \( \inf C = 1 \) です。
集合 \( C \) は上界が存在しないため、無界です。
2.4. 例題4
集合 \( D \) の最大の数は \( 2 \) なので、上限は \( \sup D = 2 \) です。
集合 \( D \) の最小の数は \( -3 \) なので、下限は \( \inf D = -3 \) です。
集合 \( D \) は上界と下界が存在するので、有界です。
3. 有界な数列
3.1. 数列の有界性
数列 \(\{a_n\}\) が有界であるとは、正の定数 \(K\) が存在して
\[ |a_n| < K \quad (n \geq 1) \]
を満たすことを指します。つまり、全ての \(n \geq 1\) に対して \(|a_n|\) が定数 \(K\) 以内に収まることを意味します。
3.2. 有界な数列
有界な数列は、値が一定の範囲内に収まるものを指します。
3.3. 有界でない数列
有界でない数列は、例えば無限に遠くへ飛んでいく感じです。
4. 数列の例題
4.1. 例題1
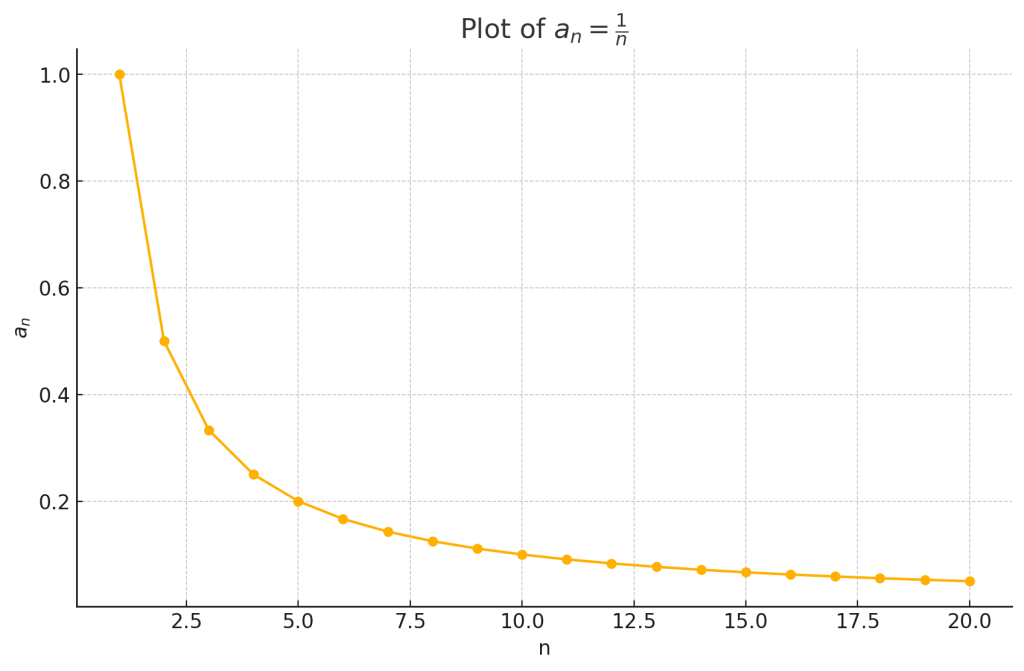
\[ a_n = \frac{1}{n} \quad (n \geq 1) \]
- この数列の上限と下限を確認しなさい。
- 数列が有界かどうかを判定しなさい。
- 数列 \(a_n = \frac{1}{n}\) の上限は、最初の項 \(a_1 = 1\) であり、下限は数列が無限に進むにつれて値が \(0\) に近づくため \(0\) です。
- 上限:\(1\)
- 下限:\(0\)
- 上限と下限がともに存在するため、この数列は有界です。
4.2. 例題2
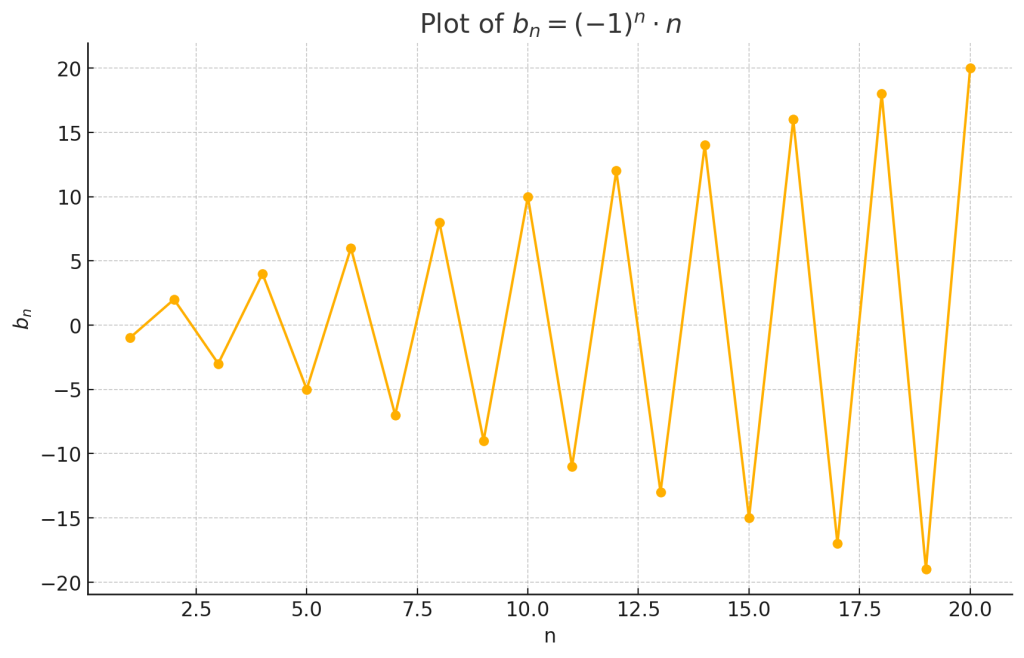
\[ b_n = (-1)^n \cdot n \quad (n \geq 1) \]
- この数列の上限と下限を確認しなさい。
- 数列が有界かどうかを判定しなさい。
- 数列 \(b_n = (-1)^n \cdot n\) の場合、奇数 \(n\) のとき \(b_n\) は負の値をとり、偶数 \(n\) のとき \(b_n\) は正の値をとります。そして、正の値は常に増加し、負の値は常に減少する。したがって、上界と下界は次のようになります。
- 上限:存在しない
- 下限:存在しない
- 上限も下限も存在しないため、この数列は有界ではありません。
4.3. 例題3
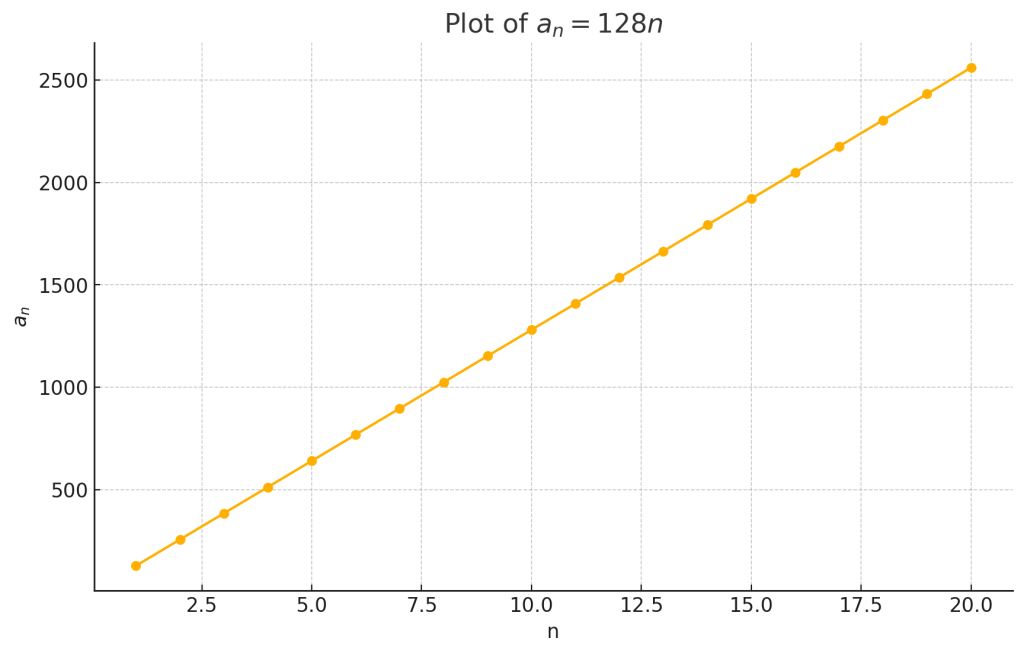
\[ a_n = 128n \quad (n \geq 1) \]
- この数列の上限と下限を確認しなさい。
- 数列が有界かどうかを判定しなさい。
- 数列 \(a_n = 128n\) の場合、\(n\) が増加すると \(a_n\) の値も無限に増加します。
- 上限:存在しない(数列は正の無限大に発散します)
- 下限:\(n = 1\) のとき、最小値 \(a_1 = 128\) です。
- 上限が存在しないため、この数列は上に有界ではありません。しかし、下限は \(128\) であるため、下に有界です。
- この数列は上に有界ではないが、下に有界です。
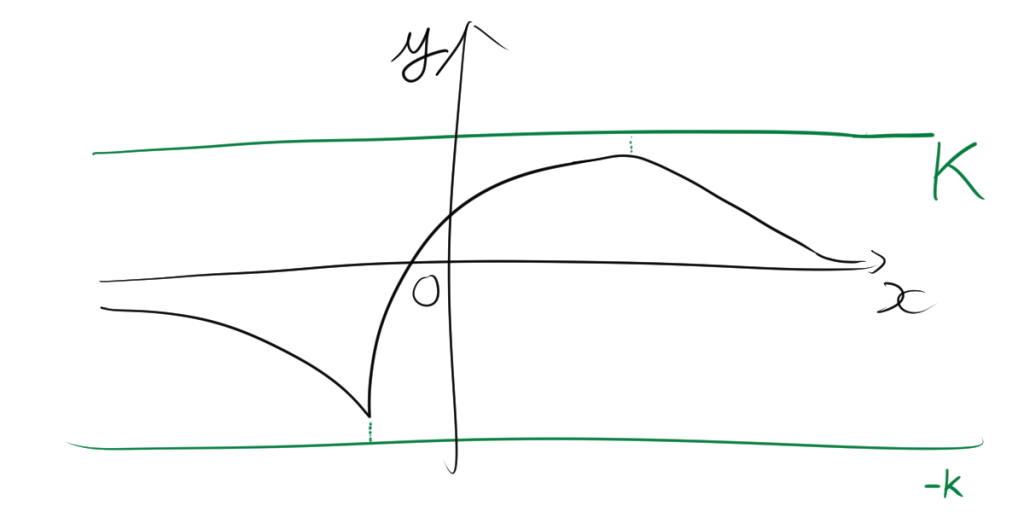
5. 有界な関数
5.1. 関数の有界性
\[ |f(x)| < K, \quad x \in A \]
が成り立つことです。つまり、関数の絶対値\( |f(x)| \) が定数 \( K \) 以内に収まることを意味します。
5.2. 有界な関数
有界な関数は、グラフが一定の範囲内に収まるものを指します。
5.3. 有界でない関数
有界でない関数は、数列と同様に無限に遠くへ飛んでいく感じです。
6. 有界な関数の例題
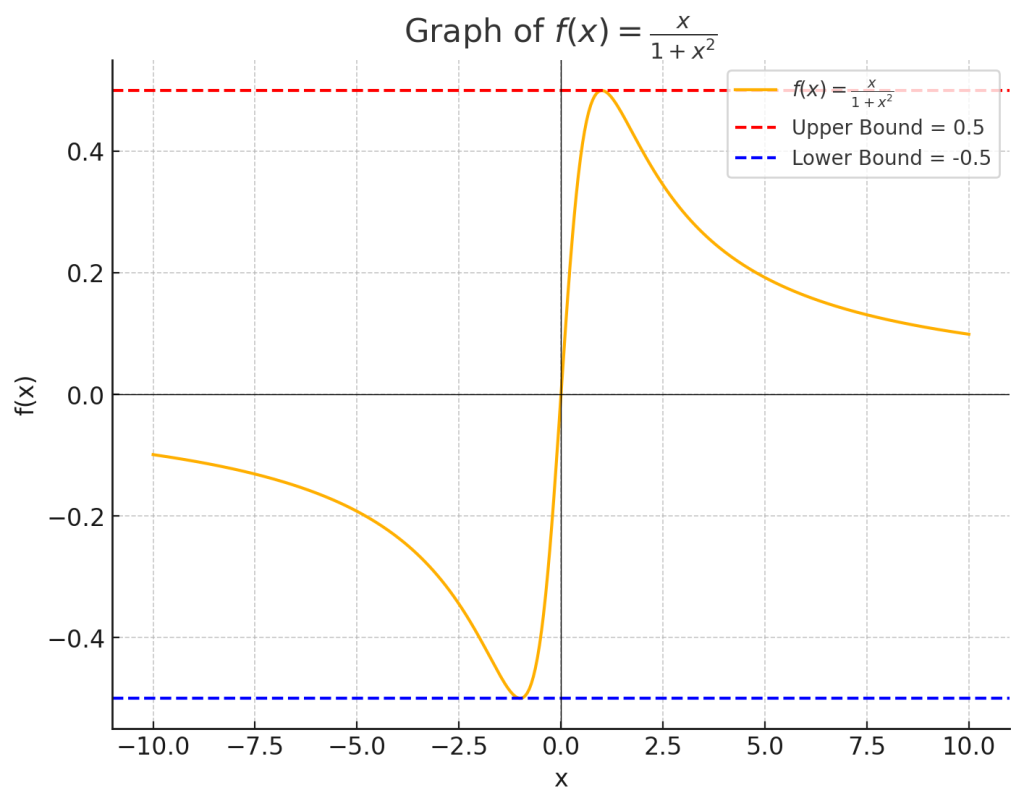
6.1. 例題1
\( f'(x) = \frac{1 – x^2}{(1+x^2)^2} \) を計算し、\( f'(x) = 0 \) を解きます。
\( 1 – x^2 = 0 \) なので、\( x = \pm 1 \) が得られます。
極値の計算を行うと次のようになります。
$$f(1) = \frac{1}{2} $$
$$f(-1) = -\frac{1}{2} $$
これらの点と \( x \to \pm\infty \) の極限を確認します。
極限の計算を行うと次のようになります。
$$\lim_{x \to \infty} \frac{x}{1+x^2} = \lim_{x \to \infty} \frac{ \frac{1}{x}}{1+ \frac{1}{x^2}} = 0$$
$$\lim_{x \to -\infty} \frac{x}{1+x^2} = \lim_{x \to -\infty} \frac{ \frac{1}{x}}{1+ \frac{1}{x^2}} = 0 $$
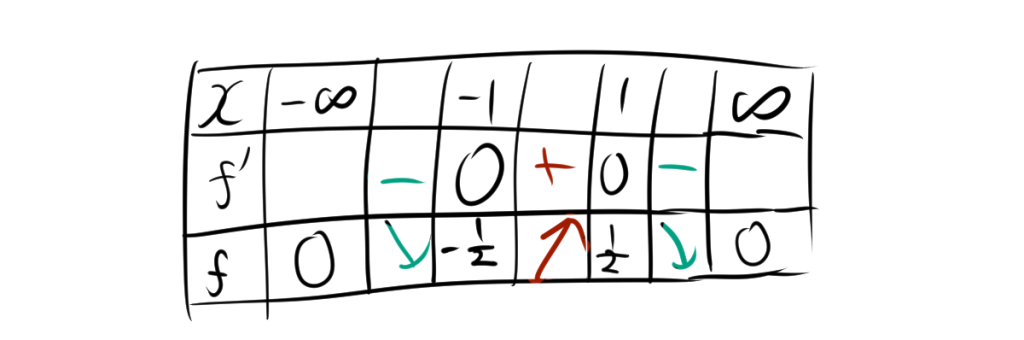
増減表を書くと次のようになります。
したがって、上限と下限は次のようになります。
上限: \( \frac{1}{2} \)
下限: \( -\frac{1}{2} \)
関数の上限が \( \frac{1}{2} \)、下限が \( -\frac{1}{2} \) であり、$|f(x)|\leq \frac{1}{2}$より、これらの範囲内で \( f(x) \) のすべての値が存在するので、この関数は有界です。
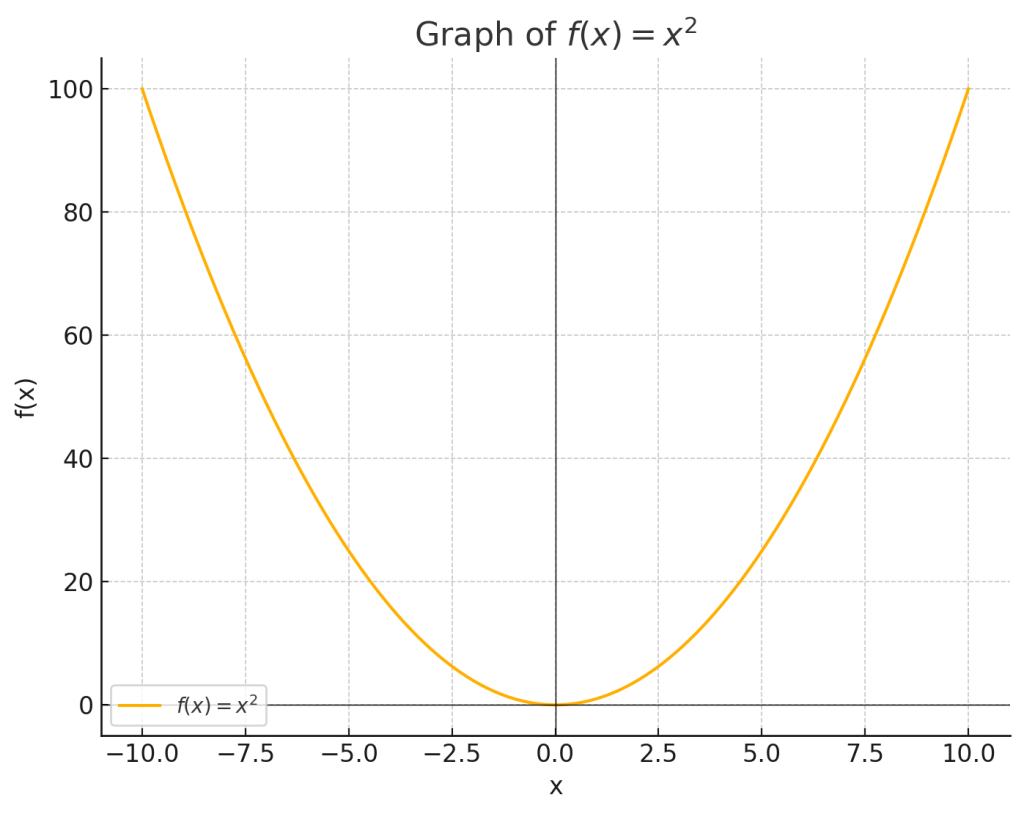
6.2. 例題2
この関数の値は常に非負であり、最小値は \( x = 0 \) のときに取られます。
極限の計算を行うと次のようになります。
$$ \lim_{x \to \infty} x^2 = \infty $$
$$ \lim_{x \to -\infty} x^2 = \infty $$
最小値の計算を行うと次のようになります。
\( f(0) = 0 \)
上限と下限については次のようになります。
下限: \( 0 \)
上限: 存在しない
下に有界ではあるが、この関数は有界ではありません。