カージオイド曲線の面積、弧長、回転体の体積、アニメーションについて

1. カージオイドとは

1.1. カージオイドのアニメーション

カージオイド (cardioid) は、円が固定された別の円に沿って転がることで生成される曲線です。エピサイクロイドの一種です。固定された円と動く円の半径の比は1:1になる。

 

2. カージオイドの性質

2.1. 直交座標におけるカージオイド

極方程式の両辺にrをかけると、

$$r^2=a(r+\cos\theta)$$

となる。$ r = \sqrt{x^2 + y^2} $、$\cos \theta = \frac{x}{r}$を用いて、極方程式を書き換えると、

$$ (\sqrt{x^2 + y^2})^2 = a\left(\sqrt{x^2 + y^2} + x\right) $$

$$ x^2 + y^2 = a\left(\sqrt{x^2 + y^2} + x\right) $$

$$ x^2 + y^2 – a x = a\sqrt{x^2 + y^2}$$

両辺を整理して二乗し、ルートを消去します。

$$ \left(x^2 + y^2 – a x\right)^2 = \left(a\sqrt{x^2 + y^2}\right)^2 $$

$$ \left(x^2 + y^2 – a x\right)^2 = a^2 (x^2 + y^2) $$

2.2. カージオイドの媒介変数表示

極方程式から、$\theta$ を媒介変数とする $x$ と $y$ の媒介変数表示を導きます。

$x=r\cos\theta,y=r\sin\theta$より、極方程式を用いると$x,y$は次のようになります。

$$x=a\cos\theta(1 + \cos \theta)$$

$$y=a\sin\theta(1 + \cos \theta)$$

2.3. カージオイドの面積

まず、\( r^2 \) を計算します。

これを代入して、

\[ r^2 = a^2\left(1 – 2\cos\theta + \frac{1 + \cos 2\theta}{2}\right) \\ = a^2\left(\frac{3}{2} – 2\cos\theta + \frac{\cos 2\theta}{2}\right) \]

面積 \( S \) は、

\[ S = \frac{1}{2} \int_0^{2\pi} a^2\left(\frac{3}{2} – 2\cos\theta + \frac{\cos 2\theta}{2}\right) d\theta \]

\[ = \frac{a^2}{2} \int_0^{2\pi} \left(\frac{3}{2} – 2\cos\theta + \frac{\cos 2\theta}{2}\right) d\theta \]

$\cos\theta$と$\cos 2\theta$の積分は0になるため、

\[  = \frac{a^2}{2} \times 3\pi+0+0 = \frac{3}{2} \pi a^2 \]

したがって、カージオイドの面積は、

\[ S = \frac{3}{2} \pi a^2 \]

2.4. カージオイドの弧長

まず、\( \frac{dr}{d\theta} \) を計算します。

\[ \frac{dr}{d\theta}=  \\ \frac{d}{d\theta}a(1 +\cos\theta) = -a\sin\theta \]

次に、 \( r^2 + \left( \frac{dr}{d\theta} \right)^2 \) を計算します。

\[ r^2 + \left( \frac{dr}{d\theta} \right)^2 = a^2(1 + \cos\theta)^2 + (-a\sin\theta)^2 = a^2[(1 + \cos\theta)^2 + \sin^2\theta] \]

展開すると、

\[ (1 + \cos\theta)^2 + \sin^2\theta = 1 + 2\cos\theta + \cos^2\theta + \sin^2\theta \]

したがって、

\[ r^2 + \left( \frac{dr}{d\theta} \right)^2 = 2a^2(1 + \cos\theta) \]

弧長の式は、

\[ L = \int_0^{2\pi} \sqrt{2a^2(1 + \cos\theta)} \, d\theta = a\sqrt{2} \int_0^{2\pi} \sqrt{1 + \cos\theta} \, d\theta \]

さらに、\( 1 + \cos\theta = 2\cos^2\left( \frac{\theta}{2} \right) \) なので、

\[ \sqrt{1 + \cos\theta} = \sqrt{2} \left| \cos\left( \frac{\theta}{2} \right) \right| \]

弧長の式より、

\[ L = a\sqrt{2} \times \sqrt{2} \int_0^{2\pi} \left| \cos\left( \frac{\theta}{2} \right) \right| d\theta = 2a \int_0^{2\pi} \left| \cos\left( \frac{\theta}{2} \right) \right| d\theta \]

積分を計算します。$ \sin\left( \frac{\theta}{2} \right)$は0から$\pi$の範囲で正であることより、

\[ \int_0^{2\pi} \left| \cos\left( \frac{\theta}{2} \right) \right| d\theta  \]

$$=2\int_0^{\pi}  \cos\left( \frac{\theta}{2} \right)  d\theta$$

$$=2\left[ 2\sin\left( \frac{\theta}{2} \right) \right]^{ \pi }_{0}$$

$$=2\times 2=4$$

したがって、

\[ L = 2a \times 4 = 8a \]

2.5. カージオイドを回転させたときの体積

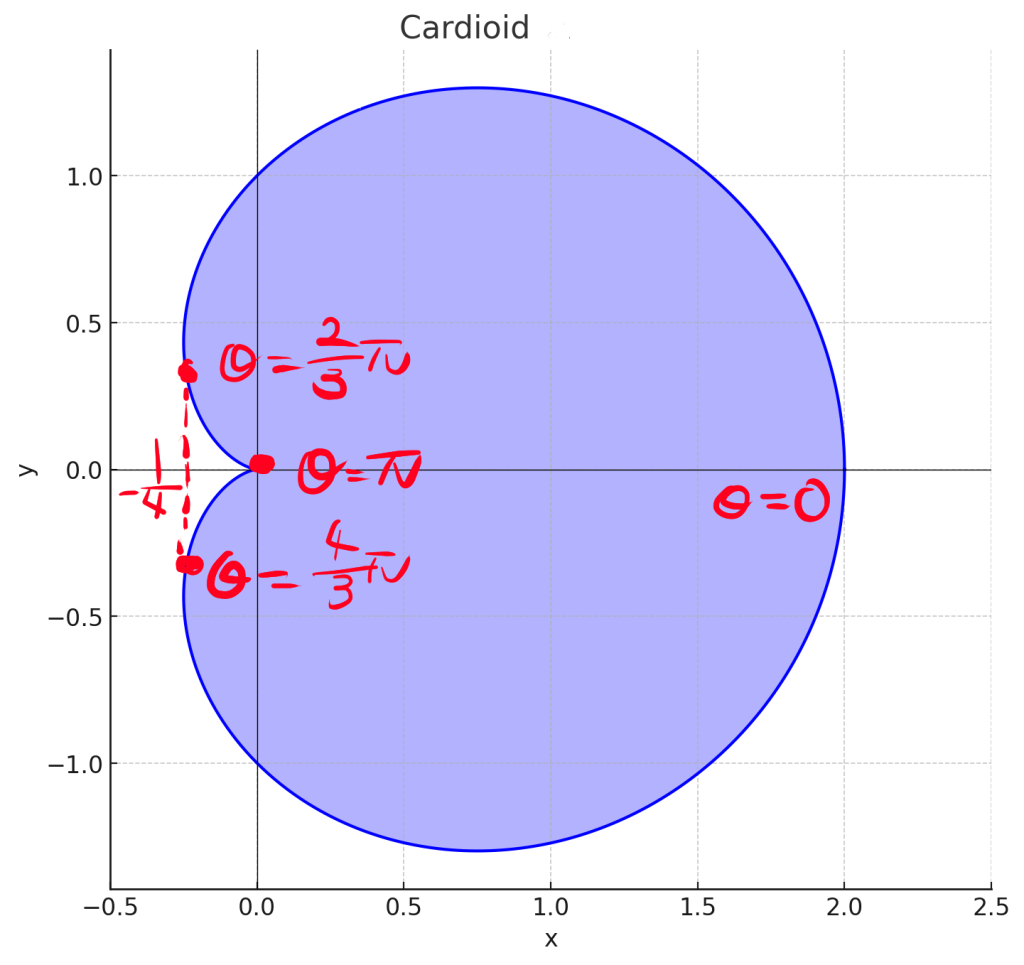
カージオイドの体積を求めるために、まず \( a=1 \) の場合を考えます。以下のようなグラフが得られます。

この図形は対称性を持っているため、上半分（ \( 0 < \theta < \pi \) の範囲）の体積を求めれば、全体の体積の半分になります。

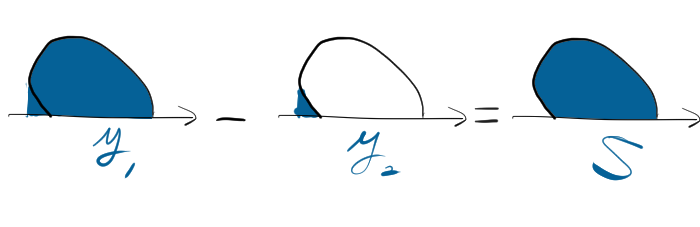
直接面積を求めると余分な部分も含まれてしまうため、求めたい面積 \( S \) を次のような図で考え、\( S = y_1 – y_2 \) とします。

• \( y_1 \) は \( 0 < \theta < \frac{2}{3}\pi \) の範囲
• \( y_2 \) は \( \frac{2}{3}\pi < \theta < \pi \) の範囲

微小区間の長さ \( dx \) は次のように表されます。 \[ dx = a(1+\cos\theta)(-\sin\theta) + a\cos\theta(-\sin\theta) d\theta \] \[ dx = -a\sin\theta (1+2\cos\theta) d\theta \]

これを用いて、媒介変数表示で積分して体積を計算します。体積 \( V \) は以下のように求められます。

\[ V = \pi \int S^2 \, dx \]

2つの領域に分けて積分を行います。 \[ V = \pi \int_{-\frac{1}{4}a}^{2a} y_1^2 \, dx – \pi \int_{-\frac{1}{4}a}^{0} y_2^2 \, dx \]

\[ V = \pi \int_{0}^{\frac{2}{3}\pi} a^2\sin^2\theta(1 + \cos \theta)^2 \cdot (-a\sin\theta (1+2\cos\theta)) \, d\theta \]

\[ -\pi \int_{\frac{2}{3}\pi}^{\pi} a^2\sin^2\theta(1 + \cos \theta)^2 \cdot (-a\sin\theta (1+2\cos\theta)) \, d\theta \]

まとめると、

\[ V = a^3\pi \int_{0}^{\pi} \sin^2\theta(1 + \cos \theta)^2 (1+2\cos\theta)\sin\theta \, d\theta \]

次に、 \( \cos\theta = t \) と置換します。

\[ dt = -\sin\theta \, d\theta \]

よって、

\[ V = a^3\pi \int_{1}^{-1} (1-t^2)(1 + t)^2 (1+2t) \, (-dt) \]

積分範囲を正の順序に戻して、 \[ V = a^3\pi \int_{-1}^{1} (1-t^2)(1 + t)^2 (1+2t) \, dt \]

積分の中身を展開します、

$$ (1 – t^2)(1 + 2t + t^2) (1+2t) = (1 + 2t – 2t^3 – t^4)(1+2t) $$

\[ = 1 + 4t + 4t^2 – 2t^3 – 5t^4 – 2t^5 \]

したがって、

\[ V = a^3\pi \int_{-1}^{1} (1 + 4t + 4t^2 – 2t^3 – 5t^4 – 2t^5) \, dt \]

偶関数と奇関数の性質を利用します。積分範囲が \([-1, 1]\) であるため、奇関数の積分は 0 になります。

したがって、

\[ V = 2a^3\pi \int_{0}^{1} (1 + 4t^2 – 5t^4) \, dt \]

\[  = 2a^3\pi \left[t+\frac{4}{3}t^3-t^5 \right]^{1}_{0} = 2a^3\pi \times \frac{4}{3} \]

したがって、カージオイドの体積は

\[ V = \frac{8}{3} a^3\pi \]