三角形の重心の証明、性質と例題について
1. 重心
2. 三角形の重心の性質
2.1. 中線を2:1に内分する
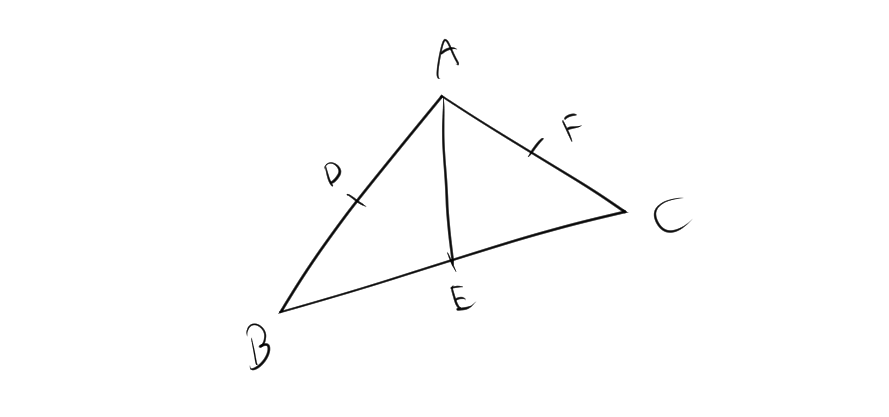
△ABCの辺AB，BC，CAの中点をそれぞれD，E，Fとします。
次の二つの場合を考えます。
- AEとDCの交点をGとする場合
- AEとBFの交点をG’とする場合
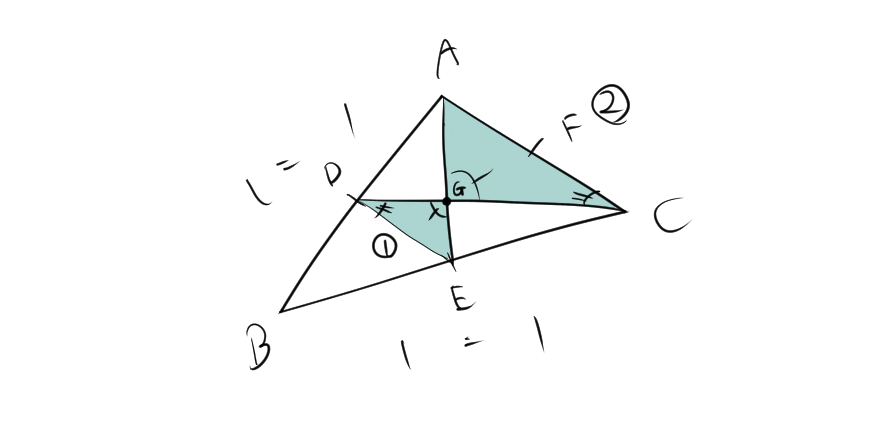
[1]AEとDCの交点をGとする場合
DとEは中線であるので、中線連結定理より、$DE:AC=1:2$、$DE/\!/AC$が成り立つ。対頂角が等しいので、$ \angle DGE= \angle CGA$となる。一方で、平行であるときに、錯覚は等しいため、$ \angle EDG= \angle ACG$となる。したがって、二つの角が等しいので、三角形DGEと三角形CGAは相似である。相似比より、
$$AG:EG=DE:CA =2:1$$
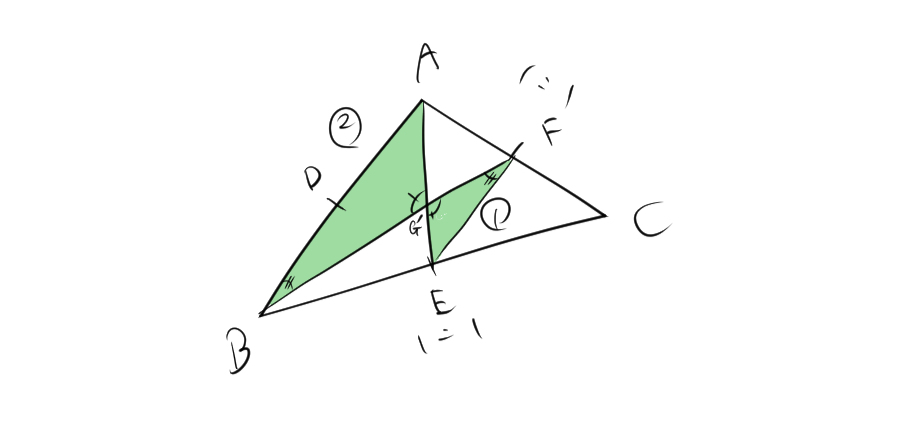
[2]AEとBFの交点をG’とする場合
FとEは中線であるので、中線連結定理より、$FE:AB=1:2$、$FE/\!/AB$が成り立つ。対頂角が等しいので、$ \angle AG’B= \angle EG’F$となる。一方で、平行であるときに、錯覚は等しいため、$ \angle EFG’= \angle ABG’$となる。したがって、二つの角が等しいので、三角形FG’Eと三角形BG’Aは相似である。相似比より、
$$AG’:EG’=FE:AB =2:1$$
[1],[2]より、GとG’は中線AEを$2:1$に内分するので、GとG’は一致します。同様に、$CG:DG=BG:GF=2:1$になるので、重心は中線を2:1に内分することがわかる。
2.2. 重心の座標
\[ G \left( \frac{x_1 + x_2 + x_3}{3}, \frac{y_1 + y_2 + y_3}{3} \right) \]
2.3. 位置ベクトル
\[ \vec{g} = \frac{\vec{a} + \vec{b} + \vec{c}}{3} \]
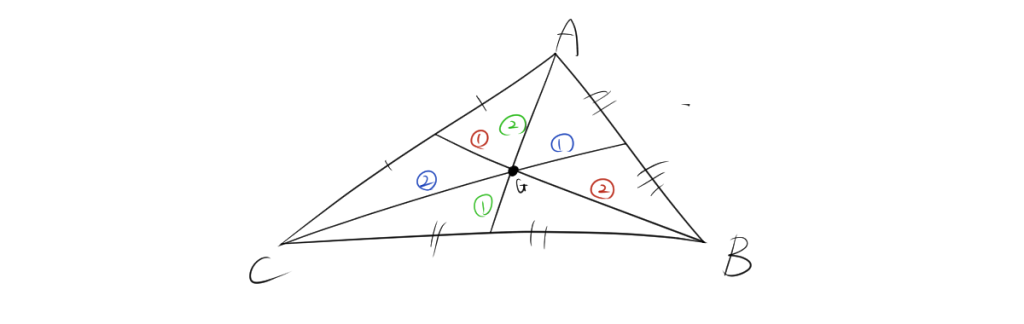
2.4. 面積比
\[ S_{\text{三角形ACG}} : S_{\text{三角形BCG}} : S_{\text{三角形ABG}} = 1:1:1\]
3. 重心の例題
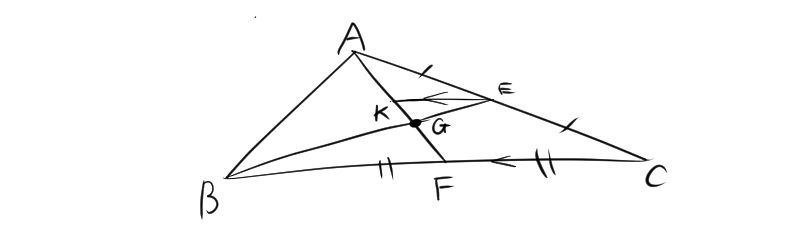Gは重心であるので、$AG:GF=2:1$となる。ABまでEKを伸ばすと、ABの中点と交わるため、その交点をMとする。したがって、中線連結定理より、
$$ME:BC=1:2$$
になる。$BC=2BF$、$ME=2KE$より、
$$ME:BC=2BF:2KE=BF:KE=1:2$$
また、
$$KG:FG=BF:KE=1:2$$
KはAFの中点になるので、$AK:KF=1:1$となる。したがって、
$$AK:KG:GF=1:\frac{1}{3}:\frac{2}{3}=3:1:2$$
$KG$の長さは
$$KG=\frac{1}{6}AB=\frac{1}{6}\cdot 144 = 24$$
