文脈自由文法と導出木、 最左導出と最右導出の性質と例について

1. 文脈自由文法とは
文脈自由文法 (Context-Free Grammar, CFG) は、形式言語理論で使われる文法の一種です。
1.1. 基本的な要素
\[ G = (N, \Sigma, R, S) \]
ここで、この数式の意味は次のようになっています。
- \( N \) (非終端記号の集合): 文法で使用される非終端記号の集合。非終端記号から文法は生成されます。
- \( \Sigma \) (終端記号の集合): 文法で使用される終端記号の集合。これらは文法の生成物であり、最終的な文字列を構成します。終端記号は展開されることはありません。
- \( P \) (生成規則の集合): 生成規則の有限集合。各生成規則は次の形式で書かれます。\[ A \rightarrow \alpha \]ここで、\( A \in N \)(非終端記号)であり、\( \alpha \in (N \cup \Sigma)^* \)(非終端記号と終端記号の列)です。つまり、非終端記号 \( A \) は終端記号と非終端記号の任意の列 \( \alpha \) に置き換えることができます。
- \( S \) (開始記号): 文法の開始記号であり、\( S \in N \) です。
この形式で定義された文法 \( G \) に基づいて、言語を生成することができます。また、この文法で生成される言語$L$は$L(G)$で表され、文脈自由言語と呼ばれます。
1.2. 文脈自由文法の例
例えば、以下のような文法を考えます。
- 非終端記号: S
- 終端記号: a, b
- 開始記号: S
- 生成規則:
- S → aSb
- S → ε (εは空文字を表します)
この文法は、左右対称な「a」と「b」のペアを生成します。例えば、「ab」「aabb」「aaabbb」などが生成されます。
2. 最左導出と最右導出
最左導出と最右導出は、文脈自由文法 (CFG) における文字列生成の方法で、非終端記号の展開順序に関する概念です。
2.1. 概要
- 最左導出: 常に左端から非終端記号を展開する。
- 最右導出: 常に右端から非終端記号を展開する。
2.2. 最左導出
最左導出とは、文字列を生成する際に、常に最も左にある非終端記号から順に生成規則を適用して展開していく方法です。具体的には、文法の規則を適用するたびに、左から右に見て最初に見つかる非終端記号を展開します。
2.2.1. 例
文法 \( G = (N, \Sigma, P, S) \) で、生成規則が以下のように与えられているとします。
- \( S \rightarrow AB \)
- \( A \rightarrow a \)
- \( B \rightarrow b \)
このとき、最左導出を使って文字列 “ab” を生成する過程は次のようになります。
\( S \)
\( \rightarrow \) \( AB \) (\( S \rightarrow AB \) の適用)
\( \rightarrow \) \( aB \) (\( A \rightarrow a \) の適用、最も左にある \( A \) を展開)
\( \rightarrow \) \( ab \) (\( \rightarrow \)0 の適用、次に最も左にある \( \rightarrow \)1 を展開)
2.3. 最右導出
最右導出とは、文字列を生成する際に、常に最も右にある非終端記号から順に生成規則を適用して展開していく方法です。具体的には、文法の規則を適用するたびに、右から左に見て最初に見つかる非終端記号を展開します。
2.3.1. 例
上記と同じ文法 \( G \) を用いた場合の最右導出は次のようになります。
\( S \)
\( \rightarrow \) \( AB \) (\( S \rightarrow AB \) の適用)
\( \rightarrow \) \( Ab \) (\( B \rightarrow b \) の適用、最も右にある \( B \) を展開)
\( \rightarrow \) \( ab \) (\( \rightarrow \)0 の適用、次に最も右にある \( \rightarrow \)1 を展開)
3. 導出木
導出木または構文解析木は、文脈自由文法 (CFG) に基づいて生成された文字列の構造を視覚的に表現する木構造です。この木は、文法規則がどのように適用されたかを階層的に示し、生成過程を理解しやすくします。
3.1. 導出木の構造
導出木は次の要素で構成されます。
- 根: 木の最上位にあるノードであり、文法の開始記号 \( S \) に対応します。
- 節: 非終端記号に対応するノードです。これらのノードには子ノードがあり、生成規則の右辺のシンボルに対応します。
- 葉: 終端記号に対応するノードで、これ以上展開されません。生成された最終的な文字列に直接対応します。
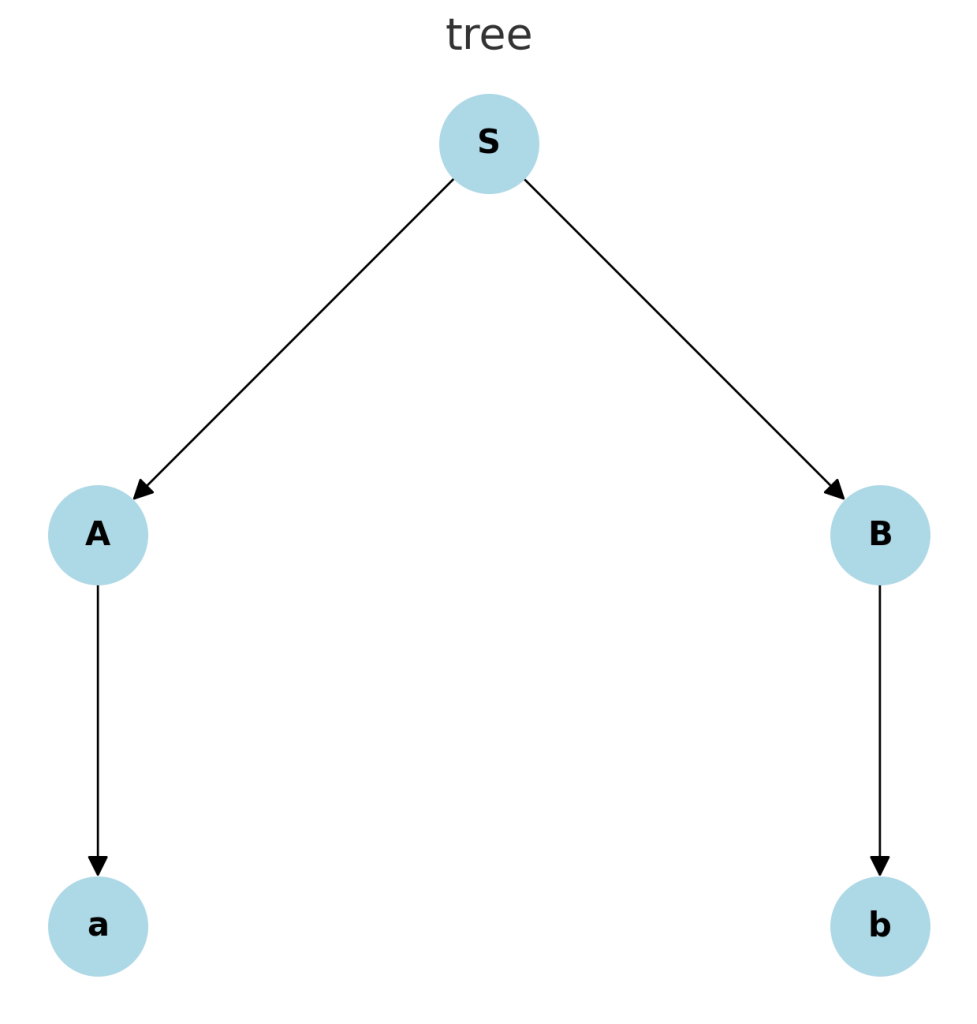
3.2. 導出木の例
以下の文法 \( G \) を考えます。
- \( S \rightarrow AB \)
- \( A \rightarrow a \)
- \( B \rightarrow b \)
この文法を使って文字列 “ab” を生成する場合の導出木は次のようになります。
3.3. 導出木の性質
- 最左導出と最右導出: 導出木は同じ文法規則の適用によって生成されますが、最左導出や最右導出に基づく異なる順序で同じ文字列を生成できます。
- 曖昧性: ある文法が曖昧である場合、同じ文字列に対して複数の異なる導出木(または構文解析木)が存在する可能性があります。これは、同じ文字列を異なる方法で生成できることを意味し、文法が曖昧でない場合、文字列に対して一意の導出木が存在します。
4. オートマトンと形式文法の対応関係
オートマトンと形式文法の対応関係は次のようになります。
| 形式文法 | オートマン |
|---|---|
| 句構造文法 | チューリングマシン |
| 文脈依存文法 | 線形有界オートマトン |
| 文脈自由文法 | プッシュダウンオートマトン |
| 正則文法(正規文法) | 有限オートマトン |