文脈自由言語でない言語とポンピング補題・uvwxy定理・例題について

1. ポンピング補題
uvwxy定理や反復補題、繰り返しの定理とも呼ばれる。文脈自由言語(Context-Free Language, CFL)ではない言語を示す方法の一つとして、「ポンピング補題」がよく使われます。
1.1. ポンピング補題
文脈自由言語に対するポンピング補題は、次のように表現できます。
- \( vxy \) の長さは \( p \) 以下。・・・ \( | vxy| \leq p \)
- \( xy \) は空でない。・・・\( |xy| > 0 \)
- \( u v^i x y^i z \) は任意の \( i \geq 0 \) に対して \( L \) に属する。・・・$u v^i w x^i y \in L$
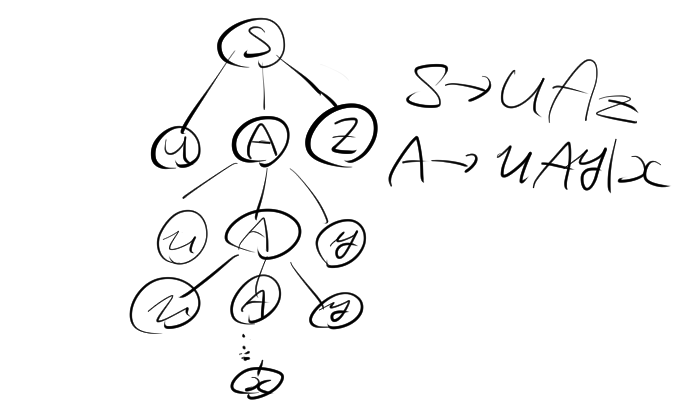
1.2. ポンピング補題のイメージ
$u v^i w x^i y$を図にすると次のようになります。
2. 文脈自由言語でない言語の例
最も有名な文脈自由言語でない言語の一つは次のものです。
\( L = \{ a^n b^n c^n \mid n \geq 1 \} \)
この言語は「同じ数の ‘a’、’b’、’c’ を含む文字列」の集合です。これは文脈自由言語ではないことがポンピング補題を使って証明できます。この言語は次の文脈依存文法で生成されることが知られています。
2.1. 文法の生成規則
言語 \( L = \{ a^n b^n c^n \mid n \geq 1 \} \) の文脈依存文法の生成規則は以下のように定義できます。
\( S \rightarrow aSBC \)
\( SB \rightarrow aBB \)
\( BB \rightarrow Bb \)
\( Bb \rightarrow bb \)
\( BC \rightarrow bC \)
\( bC \rightarrow bc \)
\( Sc \rightarrow c \)
この文法で、開始記号 \( S \) からスタートし、以下のように展開されていきます。
2.2. 生成例
例えば、\( n = 2 \) の場合の生成過程を見てみましょう。
- \( S \rightarrow aSBC \)
- \( aSBC \rightarrow aaBBBC \) (規則1適用)
- \( aaBBBC \rightarrow aabBBC \) (規則2適用)
- \( aabBBC \rightarrow aabBbC \) (規則3適用)
- \( aabBbC \rightarrow aabbBC \) (規則4適用)
- \( aabbBC \rightarrow aabbcC \) (規則5適用)
- \( aabbcC \rightarrow aabbcc \) (規則6適用)
したがって、文字列 \( aabbcc \) が生成されます。
この文脈依存文法では、終端記号が1つずつ生成され、各 \( a \) に対応する \( b \)、および各 \( b \) に対応する \( c \) が順番に生成されていくことで、言語 \( L = \{ a^n b^n c^n \mid n \geq 1 \} \) が構築されます。
3. 文脈自由文法でないことを証明
3.1. 例題1(a,b,cの数が一致する)
まず、言語 \( L = \{a^n b^n c^n \mid n > 0\} \) が文脈自由言語であると仮定します。
ここで、特に \( w = a^n b^n c^n \) という形の文字列を考えます。
反復補題によれば、文脈自由言語 \( L \) には、ある長さ \( n \) が存在し、任意の \( w \in L \) で、\( w \) を次の形に分割することができます。
\[ w = uvxyz \]
このとき、以下の条件が満たされます。
- \( v \) と \( y \) の長さは少なくとも1である(つまり、 \( |vy| > 0 \))。
- \( vxy \) の長さは \( n \) 以下である(つまり、\( |vxy| \leq n \))。
- \( u v^i x y^i z \) は任意の \( i \geq 0 \) に対して \( L \) に属する。
また、$i=0$の時の言語\( \alpha = uxz \) も言語Lに含まれる。
\( vxy \) が \( a^n b^n \) の部分に含まれる場合:
この場合、\( v \) と \( y \) はそれぞれ \( a^n \) や \( b^n \) の中のどこかに含まれます。したがって、v,x,yの長さを次のように置くことができる。
$|vxy|=2n$、$|v|=i$、$|x|=2n-i-j$、$|y|=j$とする。
ここで、言語$\alpha=uxz$について考える。
\( \alpha=uxz=a^{n-i} b^{n-j} c^n \)
のような形になります。$a,b,c$の数が一致しないので、 \( L \) には属しません。
\( vxy \) が \( b^n c^n \) の部分に含まれる場合:
この場合、\( v \) と \( y \) はそれぞれ \( b^n \) や \( c^n \) の中のどこかに含まれます。したがって、v,x,yの長さを次のように置くことができる。
$|vxy|\leq 2n$、$|v|=i$、$|x|\leq 2n-i-j$、$|y|=j$とする。
ここで、言語$\alpha=uxz$について考える。
\( \alpha=uxz=a^{n} b^{n-i} c^{n-j} \)
のような形になります。$a,b,c$の数が一致しないので、 \( L \) には属しません。
よって、仮定に矛盾するため、文脈自由文法でない。
3.2. 例題2(同じ言語が続く)
まず、言語 \( L = \{a^n b^n c^n \mid n > 0\} \) が文脈自由言語であると仮定します。
ここで、特に \( w = a^n b^n a^nb^n \) という形の文字列を考えます。
反復補題によれば、文脈自由言語 \( L \) には、ある長さ \( n \) が存在し、任意の \( w \in L \) で、\( w \) を次の形に分割することができます。
\[ w = uvxyz \]
このとき、以下の条件が満たされます。
- \( v \) と \( y \) の長さは少なくとも1である(つまり、 \( |vy| > 0 \))。
- \( vxy \) の長さは \( n \) 以下である(つまり、\( |vxy| \leq n \))。
- \( u v^i x y^i z \) は任意の \( i \geq 0 \) に対して \( L \) に属する。
また、$i=0$の時の言語\( \alpha = uxz \) も言語Lに含まれる。
\( vxy \) が 最初の\( a^n b^n \) の部分に含まれる場合:
この場合、\( v \) と \( y \) はそれぞれ \( a^n \) や \( b^n \) の中のどこかに含まれます。したがって、v,x,yの長さを次のように置くことができる。
$|vxy|=2n$、$|v|=i$、$|x|=2n-i-j$、$|y|=j$とする。
ここで、言語$\alpha=uxz$について考える。
\( \alpha=uxz=a^{n-i} b^{n-j} a^nb^n\)
のような形になります。$a,b$の数が一致しないので、 \( L \) には属しません。
\( vxy \) が 最初の\( b^na^n \) の部分に含まれる場合:
この場合、\( v \) と \( y \) はそれぞれ \( b^n \) や \( a^n \) の中のどこかに含まれます。したがって、v,x,yの長さを次のように置くことができる。
$|vxy|=2n$、$|v|=i$、$|x|=2n-i-j$、$|y|=j$とする。
ここで、言語$\alpha=uxz$について考える。
\( \alpha=uxz=a^{n} b^{n-i} a^{n-j}b^n\)
のような形になります。$a,b$の数が一致しないので、 \( L \) には属しません。
\( vxy \) が 後の\( a^nb^n \) の部分に含まれる場合:
この場合、\( v \) と \( y \) はそれぞれ \( a^n \) や \( b^n \) の中のどこかに含まれます。したがって、v,x,yの長さを次のように置くことができる。
$|vxy|\leq 2n$、$|v|=i$、$|x|\leq 2n-i-j$、$|y|=j$とする。
ここで、言語$\alpha=uxz$について考える。
\( \alpha=uxz=a^{n} b^{n} a^{n-i}b^{n-j}\)
のような形になります。$a,b$の数が一致しないので、 \( L \) には属しません。
よって、仮定に矛盾するため、文脈自由文法でない。
3.3. 例題3(言語の長さが素数)
まず、言語 \( L = \{w \in \Sigma^* \mid |w| \text{は素数}\} \) が文脈自由言語であると仮定します。
文脈自由言語 \( L \) に対して、ポンピング補題を適用すると、ある長さ \( |w| \geq n \) の文字列 \( w \) について、次の条件を満たす \( u, v, x, y, z \) が存在します。
1. \( w = uvxyz \)
2. \( |vxy| \leq n \)
3. \( |vy| > 0 \)
4. 任意の \( k \geq 0 \) に対して \( u(v^k)x(y^k)z \in L \)
次に、言語 \( L \) の定義に基づき、任意の \( k \) に対して、文字列 \( uv^kxy^kz \) の長さは素数である必要があります。具体的には、次の式が成り立ちます。
\[ |u(v^k)x(y^k)z| = |uxz| + k|vy| \]
ここで、\( |uxz| = m \) とおきます。
\( m = 0 \) の場合、\( |u(v^k)x(y^k)z| = k|vy| \) となり、\( k > 2 \) のとき \( k|vy| \) は素数ではありません。
\( m = 1 \) の場合、\( k = 0 \) のとき \( |uv^kxy^kz| = 1 \) となり、これは素数でありません。
\( m > 1 \) の場合、\( k = m \) のとき \( |uv^kxy^kz| = m(1 + |vy|) \) となり、これは素数ではありません。
したがって、どのケースにおいても、ポンピング補題の適用により、言語 \( L \) の文字列の長さがすべて素数であるという保証は得られません。よって、この言語 \( L \) は文脈自由言語ではないです。