カイ(χ)2乗分布について!ガンマ関数と確率密度関数の関連性

1. χ²分布とは
χ²分布の確率変数は、k個の独立した標準正規分布(平均0、分散1)の二乗和の分布です。つまり、Z₁, Z₂, …, Zₖを独立した標準正規分布に従う確率変数とすると、χ²分布は次のように定義されます。
\[ X = Z_1^2 + Z_2^2 + \cdots + Z_k^2 \]
このXは自由度kのχ²分布に従います。
1.1. 基本的な性質
- 自由度 (degrees of freedom, df): χ²分布は自由度(df)というパラメータによって特徴づけられます。自由度は、観測データの数を制約条件として表します。
- 形状: 自由度が1のときは右に尖った形状をしており、分布の形状が右に広がり、常に正の値しか取りません。
2. χ²分布の確率密度関数(PDF)
\[ \large f(x; k) = \begin{cases} \frac{1}{2^{\frac{k}{2}} \Gamma(\frac{k}{2})} x^{\frac{k}{2} – 1} e^{-\frac{x}{2}} & (x > 0) \\ 0 & (x \leq 0) \end{cases} \]
ここで、
- \( x \) は非負の実数( \( x \geq 0 \) )。
- \( k \) は自由度。
- \( \Gamma \) はガンマ関数です。特に、自然数 \( n \) に対して、 \( \Gamma(n) = (n-1)! \)。
2.1. ガンマ関数
ガンマ関数 \( \Gamma(z) \) は次のように定義されます。
\[ \Gamma(z) = \int_0^\infty t^{z-1} e^{-t} \, dt \]
2.2. 自由度k=2のときの例
例えば、自由度 \( k = 2 \) の場合、確率密度関数は次のようになります。
\[ f(x; 2) = \frac{1}{2 \Gamma(1)} x^{1-1} e^{-x/2} \]
ここで、\( \Gamma(1) = 1 \) ですので、
\[ f(x; 2) = \frac{1}{2} e^{-\frac{x}{2}} \]
これは指数分布の$\lambda=\frac{1}{2}$の確率密度関数と一致します。
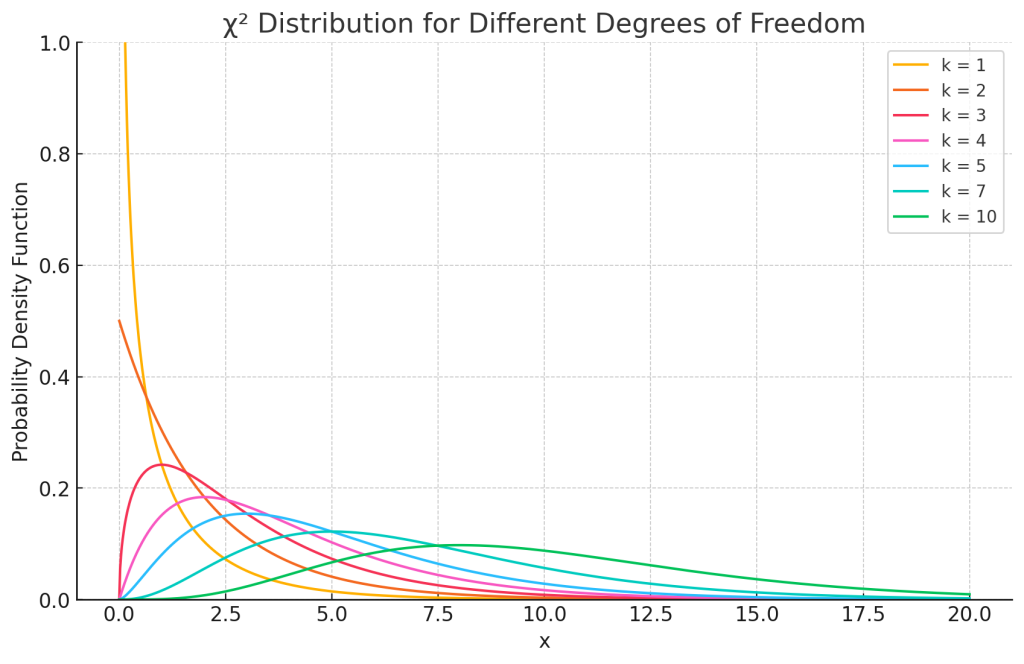
2.3. プロット
自由度によって異なる形状の確率密度関数をプロットすると、χ²分布の性質がわかりやすくなります。自由度が増えるにつれて、分布の形状が右に広がります。
3. 期待値と分散
自由度を \( n \) とした場合、カイ二乗分布 \( \chi^2(n) \) の期待値と分散は以下のようになります。
- 期待値: \( E[X] = n \)
- 分散: \( \mathrm{Var}(X) = 2n \)
以下、2通りの方法で導出を示します。
4. モーメント母関数を用いる方法
カイ二乗分布のモーメント母関数は
\[ M_X(t) = E[e^{tX}] = (1-2t)^{-n/2}, \quad t < \frac{1}{2}, \]
と表されます。
4.1. 期待値の導出
まず \( M_X(t) \) の1階微分 \( M’_X(t) \) を求めます。対数を取ってから微分すると、
\[ \ln M_X(t) = -\frac{n}{2} \ln(1-2t) \]
これを \(t\) で微分すると、
\[ \frac{M’_X(t)}{M_X(t)} = -\frac{n}{2} \cdot \frac{-2}{1-2t} = \frac{n}{1-2t} \]
よって、
\[ M’_X(t) = \frac{n}{1-2t}\, M_X(t) \]
\(t=0\) で評価すると、
\[ E[X] = M’_X(0) = \frac{n}{1} \cdot M_X(0) = n \]
4.2. 分散の導出
次に、2階微分 \( M”_X(t) \) を求めて \( E[X^2] = M”_X(0) \) を計算します。
すでに求めた1階微分は
\[ M’_X(t) = \frac{n}{1-2t} (1-2t)^{-n/2} = n (1-2t)^{-n/2-1} \]
これを \(t\) で微分すると、
\[ M”_X(t) = n\left(-\left(\frac{n}{2}+1\right)\right)(-2)(1-2t)^{-n/2-2} \]
整理すると、
\[ M”_X(t) = 2n\left(\frac{n}{2}+1\right)(1-2t)^{-n/2-2} = n(n+2) (1-2t)^{-n/2-2} \]
\(t=0\) で評価すると、
\[ E[X^2] = M”_X(0) = n(n+2) \]
よって、分散は
\[ \mathrm{Var}(X) = E[X^2] – (E[X])^2 = n(n+2) – n^2 = 2n \]
5. ガンマ分布としての性質を利用する方法
カイ二乗分布は、形状パラメータ \(\alpha = \frac{n}{2}\) と尺度パラメータ \(\beta = 2\) のガンマ分布 \(\Gamma(\alpha,\beta)\) に一致します。ガンマ分布の場合、
- 期待値: \[ E[X] = \alpha \beta, \]
- 分散: \[ \mathrm{Var}(X) = \alpha \beta^2, \]
となるので、\(\alpha = \frac{n}{2}\) および \(\beta = 2\) を代入すると、
- 期待値: \[ E[X] = \frac{n}{2} \times 2 = n, \]
- 分散: \[ \mathrm{Var}(X) = \frac{n}{2} \times 2^2 = 2n \]