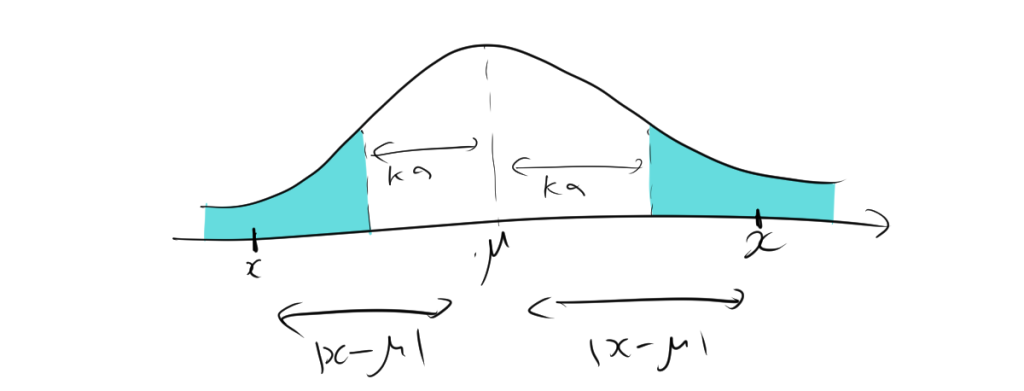
連続型と離散型のチェビシェフの不等式の証明について

はるか

チェビシェフの不等式って、聞いたことある？

ふゅか

うん、あるよ！分布が未知でも確率変数がどれだけ期待値から離れるかを教えてくれるんだよね。

1. チェビシェフの不等式

チェビシェフの不等式は連続型、離散型の両方で成り立ちます。

1.1. 連続型の場合のチェビシェフの不等式の証明

分散 \(\sigma^2\) は次のように定義されます。 \[ \sigma^2 = \int_{-\infty}^{\infty} (x – \mu)^2 f(x) dx \] ここで、\(f(x)\) は \(X\) の確率密度関数です。

\(|X – \mu| \geq k\sigma\) となる領域 \(I = \{x \mid |x – \mu| \geq k\sigma\}\) を考えます。すると$f(x)\geq 0$より

\[ \sigma^2 = \int_{-\infty}^{\infty} (x – \mu)^2 f(x) dx \geq\int_{I} (x – \mu)^2 f(x) dx \] ですが、領域 \(I\) では \(|x – \mu| \geq k\sigma\) であるため、 \[ \int_{I} (x – \mu)^2 f(x) dx \geq \int_{I} k^2 \sigma^2 f(x) dx \]

したがって、 \[ k^2 \sigma^2 \int_{I} f(x) dx \leq \sigma^2 \] ここで、\(\int_{I} f(x) dx = P(|X – \mu| \geq k\sigma)\) なので、 \[ k^2 \sigma^2 P(|X – \mu| \geq k\sigma) \leq \sigma^2 \]

両辺を \(\sigma^2\) で割って、 \[ k^2 P(|X – \mu| \geq k\sigma) \leq 1 \] したがって、 \[ P(|X – \mu| \geq k\sigma) \leq \frac{1}{k^2} \]

したがって、連続型の場合のチェビシェフの不等式は成り立ちます。

はるか

これで、連続型の場合のチェビシェフの不等式が証明できた。

ふゅか

次は離散型の証明ね。

1.2. 離散型の場合のチェビシェフの不等式の証明

分散 \(\sigma^2\) は次のように定義されます。 \[ \sigma^2 = \sum_{i} (x_i – \mu)^2 P(X = x_i) \] ここで、\(x_i\) は \(X\) の取りうる値で、\(P(X = x_i)\) はその確率です。また、$P(x)$は$X$の確率質量関数です。

\(|X – \mu| \geq k\sigma\) となる領域 \(I = \{i \mid |x_i – \mu| \geq k\sigma\}\) を考えます。すると、 \[ \sum_{i \in I} (x_i – \mu)^2 P(X = x_i) \leq \sigma^2 \] ですが、領域 \(I\) では \(|x_i – \mu| \geq k\sigma\) であるため、 \[ \sum_{i \in I} (x_i – \mu)^2 P(X = x_i) \geq \sum_{i \in I} k^2 \sigma^2 P(X = x_i) \]

したがって、 \[ k^2 \sigma^2 \sum_{i \in I} P(X = x_i) \leq \sigma^2 \] ここで、\(\sum_{i \in I} P(X = x_i) = P(|X – \mu| \geq k\sigma)\) なので、 \[ k^2 \sigma^2 P(|X – \mu| \geq k\sigma) \leq \sigma^2 \]

両辺を \(\sigma^2\) で割って、 \[ k^2 P(|X – \mu| \geq k\sigma) \leq 1 \] したがって、 \[ P(|X – \mu| \geq k\sigma) \leq \frac{1}{k^2} \]

したがって、離散型の場合のチェビシェフの不等式は成り立ちます。

ふゅか

うん、連続型と同じように証明できたね！これでチェビシェフの不等式の証明が完了したね。

はるか

はい、これで終了。