複素数とは？実部と虚部、純虚数と実数、例題について

はるか

複素数って何か知ってる？

ふゅか

もちろん！複素数は、実数と虚数を組み合わせた数のことだよ。例えば、\(3000 + 4i\)みたいに表されるね。

1. 複素数とは何か？

複素数とは、実数だけでは表せない数を取り扱うために導入された数のことです。実数と虚数を組み合わせたもので、一般的な形は次のように表されます。

\[ z = a + bi \]

ここで、\(a\)と\(b\)は実数であり、\(i\)は「虚数単位」と呼ばれるもので、次の性質を持っています。

\[ i^2 = -1 \]

1.1. 複素数の構成要素

複素数は2つの部分から構成されます。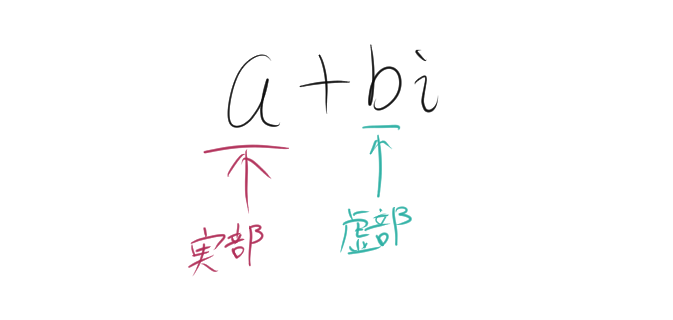実部・・・\(a\)の部分。これは「実部」と呼ばれ、\(a\)は実数です。

虚部・・・$i$の係数\(b\)の部分。これは「虚部」と呼ばれ、\(b\)は実数です。

例えば、複素数 \(3 + 4i\) では、実部は \(3\)、虚部は \(4\) です。

2. 純虚数と実数

ふゅか

ねぇ、純虚数ってどんなものか説明できる？

はるか

実部がゼロで、虚数部分だけがあるやつ。例えば、\(3214i\)とか\(-20i\)。

ふゅか

そう！一方で、実数は虚数部分がゼロになる複素数だね。

純虚数とは、実数部分が0で虚数部分のみを持つ複素数のことです。形としては \( ai \) のように表され、ここで \( a \) は実数で、\( i \) は虚数単位（\( i^2 = -1 \)）です。例えば、\( 3i \)、\(-2i\) などが純虚数に該当します。

一方で実数とは、虚数部分が0の複素数のことです。これは私たちが日常的に使う数で、負の数、正の数、0、分数、小数などすべてを含みます。例えば、\( 5 \)、\(-3\)、\( 0 \)、\( 1.5 \) などが実数です。

3. 例題

3.1. 例題 1

• 実部: \(  3 \)
• 虚部: \(  4 \)

3.2. 例題 2

• 実部: \( -2 \)
• 虚部: \(  -5 \)

3.3. 例題 3

• 実部: \( 7 \)
• 虚部: \(  0 \)

3.4. 例題 4

• 実部: \(  0 \)
• 虚部: \(  6 \)

3.5. 例題 5

• 実部: \(  -3 \)
• 虚部: \( 2 \)