余弦定理とは？意味と2通りの証明、例題について
1. 余弦定理
余弦定理は、三角形の2辺の長さと1つの角度の間の関係を表す定理です。
任意の三角形ABCに対して、以下のように成り立ちます。
\[\begin{align*} a^2 &= b^2+c^2-2bc\cos A \\ b^2 &= a^2+c^2-2ac\cos B \\ c^2 &= a^2 + b^2 – 2ab \cos C \end{align*}\]
ここで、\(a\), \(b\), \(c\) は三角形の各辺の長さです。
余弦定理は、三角形の辺の長さが分かっているときに角度を求めたり、角度が分かっているときに辺の長さを求めたりするのに使われます。また、鋭角三角形や鈍角三角形、直角三角形のどれに対しても適用することができます。直角三角形の場合、この余弦定理はピタゴラスの定理\[ c^2 = a^2 + b^2 \]に帰着します。一方で、正弦定理は三角形の辺とその対角の角のsinが一定の値になることを示しています。
2. 証明
2.1. 垂線を利用した証明
垂線を下す方法を用いて、余弦定理の証明を行います。三角形 \(ABC\) を考え、辺 \(a\), \(b\), \(c\) と、それぞれの角 \(A\), \(B\), \(C\) に対応するものとします。
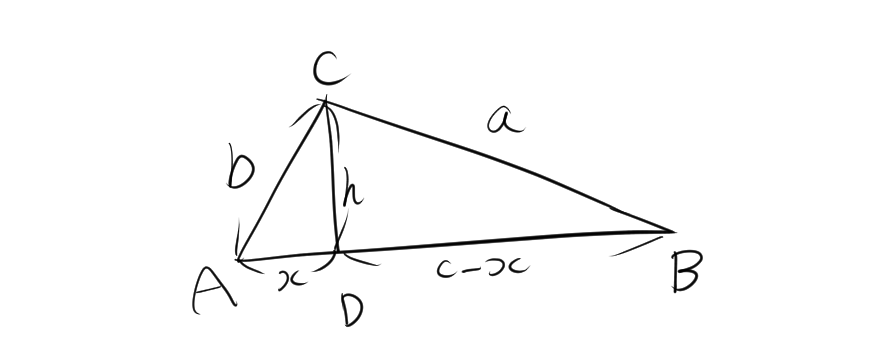
[1]角Aが鋭角であるとき、三角形 \(ABC\) の頂点 \(C\) から辺 \(AB\) に垂線を下ろし、その足を \(D\) とします。この垂線は辺 \(AB\) を2つの部分に分割し、それぞれの長さを \(AD = x\) と \(DB = c – x\) とします。さらに、垂線の長さを \(h\) とします。
三角形 \(BCD\) はそれぞれ直角三角形であるため、三平方の定理を利用すると
$$\begin{align*} h^2 + (c – x)^2 &= a^2 \quad \text{(三角形 \(BCD\) におけるピタゴラスの定理)} \end{align*}$$
\(x\) の値を求めるために、三角形 \(ACD\) における \(x\) の値を余弦を使って表します。角 \(A\) の余弦は以下のように表されます。
\[ \cos A = \frac{x}{b} \]
したがって、\(x = b \cos A\) です。また、$h=b\sin A$より、$h^2=b^2(1-\cos^2 A)$であるので、三角形BCDの三平方の定理より、
$$\begin{align*} a^2 &= h^2 + (c – x)^2 \\ a^2 &= b^2 (1 – \cos^2 A) + (c – b \cos A)^2 \\ a^2 &= b^2 – b^2 \cos^2 A + c^2 – 2bc \cos A + b^2 \cos^2 A \\ a^2 &= b^2 + c^2 – 2bc \cos A \end{align*}$$
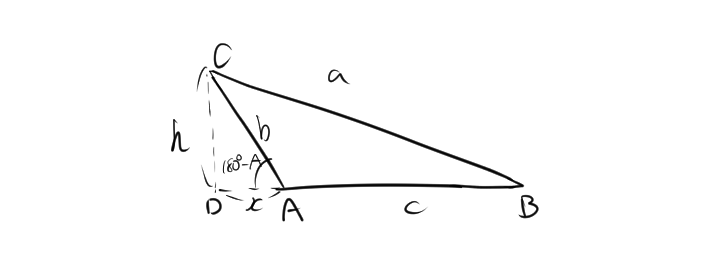
[2]次に、角Aが鈍角であるとき、
三角形 \(BCD\) はそれぞれ直角三角形であるため、三平方の定理を利用すると
$$\begin{align*} h^2 + (c + x)^2 &= a^2 \quad \text{(三角形 \(BCD\) における三平方の定理)} \end{align*}$$
\(x\) の値を求めるために、三角形 \(ACD\) における \(x\) の値を余弦を使って表します。角 \(180^\circ – A\) の余弦は以下のように表されます。
\[ \cos (180^\circ – A) =-\cos A= \frac{x}{b} \]
したがって、\(x = -b \cos A\) です。また、$h=b\sin(180^\circ -A)=b\sin A$より、$h^2=b^2(1-\cos^2 A)$であるので、三角形BCDの三平方の定理より、
$$\begin{align*} a^2 &= h^2 + (c + x)^2 \\ a^2 &= b^2 (1 – \cos^2 A) + (c – b \cos A)^2 \\ a^2 &= b^2 – b^2 \cos^2 A + c^2 – 2bc \cos A + b^2 \cos^2 A \\ a^2 &= b^2 + c^2 – 2bc \cos A \end{align*}$$
[1]、[2]により、余弦定理が成り立つことが示されました。
2.2. ベクトルを利用した証明
次のようなベクトルを利用した三角形を考えます。
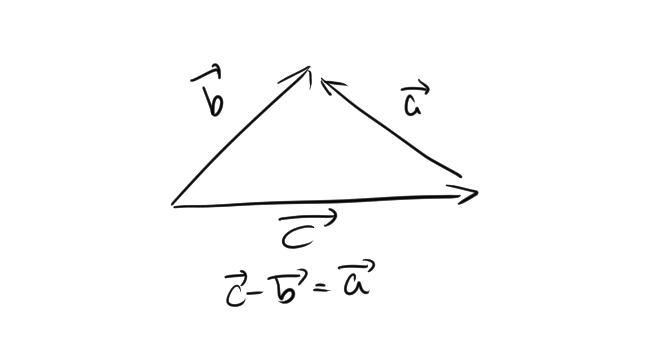ここで 、$|\vec{a}| =a,|\vec{b}| =b,|\vec{c}| =c$となります。また、 $\vec{c} – \vec{b}=\vec{a}$となります。辺 \( \vec{c} – \vec{b} \) の長さの二乗を考えます。bとcを挟む角をAとする。
\[ |\vec{c} – \vec{b}|^2 = (\vec{c} – \vec{b}) \cdot (\vec{c} – \vec{b}) \]
これを展開すると、
\[ |\vec{c} – \vec{b}|^2 = \vec{c} \cdot \vec{c} – 2 \vec{b} \cdot \vec{c} + \vec{b} \cdot \vec{b} \]
ここで、\(\vec{c} \cdot \vec{c} = |\vec{c}|^2 = c^2\)、\(\vec{b} \cdot \vec{b} = |\vec{b}|^2 = b^2\) として、さらに \(\vec{b} \cdot \vec{c} = |\vec{b}| |\vec{c}| \cos \theta = bc \cos \A\) を代入します。
\[ |\vec{c} – \vec{b}|^2 = c^2 + b^2 – 2bc \cos A\]
したがって、$|\vec{a}|^2= |\vec{c} – \vec{b}|^2$より
\[ a^2 = c^2 + b^2 – 2cb \cos A \]
となります。
3. 例題
3.1. 例題 1：Cが鋭角のとき
余弦定理を使い、値を代入して計算します。
\[ \begin{align*} c^2 &= 7^2 + 10^2 – 2 \times 7 \times 10 \times \cos 60^\circ \\ &= 49 + 100 – 2 \times 7 \times 10 \times \frac{1}{2} \\ &= 149 – 70 \\ &= 79 \\ c &= \sqrt{79} \end{align*} \]
3.2. 例題 2：余弦を求める
余弦定理を使って角 \(\cos C\)を求めます。
\[ \begin{align*} 10^2 &= 5^2 + 8^2 – 2 \times 5 \times 8 \times \cos C \\ 100 &= 25 + 64 – 80 \cos C \\ 100 &= 89 – 80 \cos C \\ 80 \cos C &= 89 – 100 \\ 80 \cos C &= -11 \\ \cos C &= -\frac{11}{80} \end{align*} \]
3.3. 例題 3：Cが鈍角の場合
余弦定理を使い、値を代入して計算します。
\[ \begin{align*} c^2 &= 12^2 + 9^2 – 2 \times 12 \times 9 \times \cos 120^\circ \\ &= 144 + 81 – 2 \times 12 \times 9 \times \left( -\frac{1}{2} \right) \\ &= 144 + 81 + 108 \\ &= 333 \\ c &= \sqrt{333} \end{align*} \]
