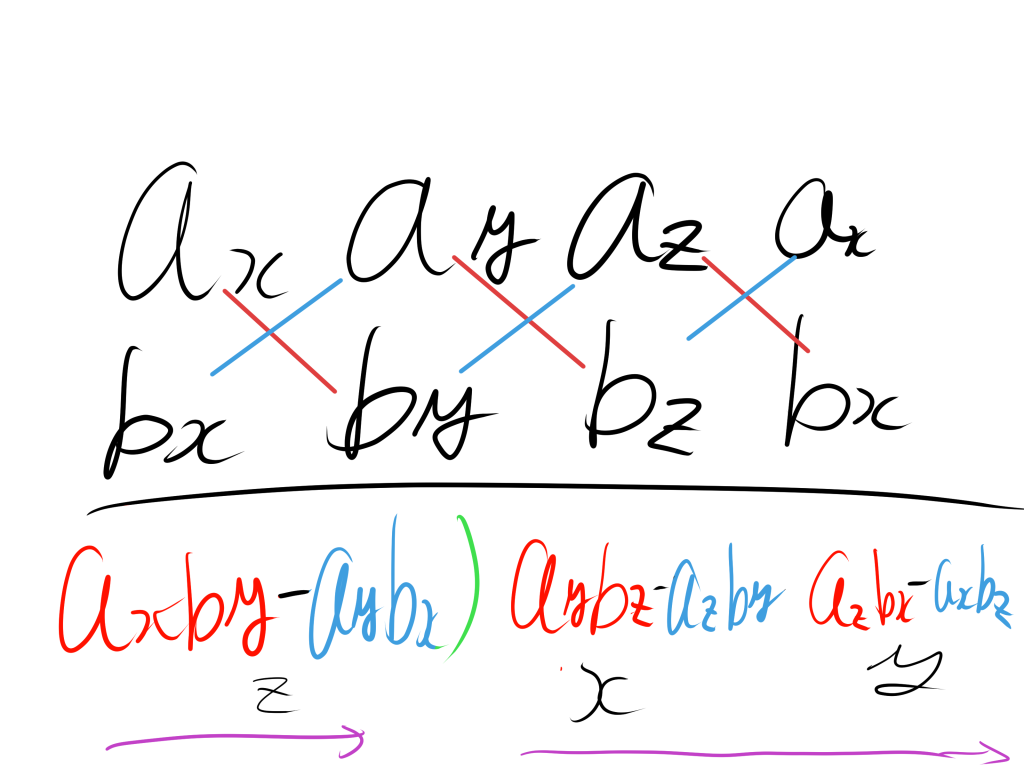外積の計算方法をマスターする！例題解説付きの計算方法と大きさの解説

ふゅか

外積はクロス積とも呼ばれることがあるわ！平行四辺形の面積を求めるのにも使えるの。今日は外積の計算方法を詳しく解説するね♪

はるか

計算方法や例題もある。

1. 外積の成分表示

1.1. 外積の計算方法を忘れてしまう方へ

以下の図のような計算方法をおすすめします。

ふゅか

もし外積の計算方法を忘れてしまったら、この図を参考にするといいわ。

言葉で表すと、外積で求めることができるそれぞれの成分は、

$$赤い線の方向上にある成分の積-青い線の方向上にある成分の積$$

となります。また、図に緑色の線がある理由は、真ん中の計算がx座標であることを示していて、その右はy座標、そして、左がz座標であるからです。

1.2. 外積の計算問題

$ \vec{a} \times \vec{b} = \begin{bmatrix} a_y b_z – a_z b_y \\ a_z b_x – a_x b_z \\ a_x b_y – a_y b_x \end{bmatrix} $を用いて、計算を行うと、

$ \vec{a} \times \vec{b} = \begin{bmatrix} 3\times (-3) – 2\times 4 \\ 4\times (-1) – 2\times (-3) \\ 2\times 2 – 3\times (-1) \\ \end{bmatrix} $

$= \begin{bmatrix} -17 \\ 2 \\ 7 \\ \end{bmatrix} $

よって、$ \vec{a} \times \vec{b} = \begin{bmatrix} -17 \\ 2 \\ 7 \\ \end{bmatrix}$である。

先ほど図を用いて紹介した外積の計算方法を用いると以下のようになる。

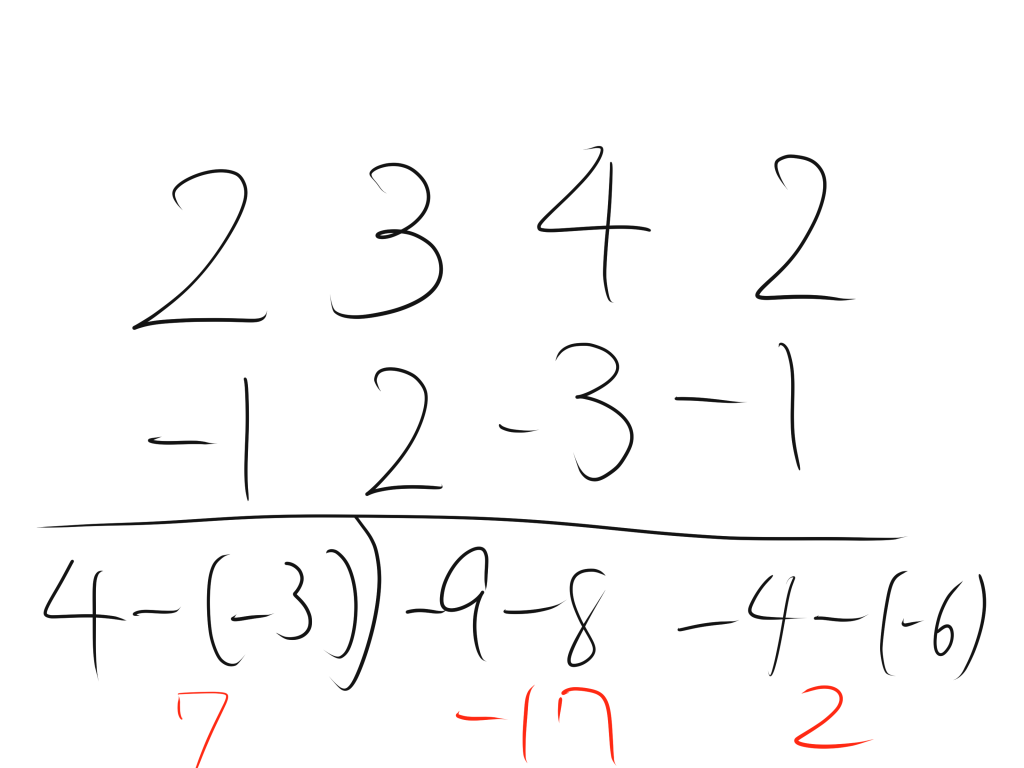
2. 外積の大きさ

はるか

外積の大きさは、ベクトルで作られる平行四辺形の面積とも関係しているんだ。

ふゅか

その通り！$|\vec{a}\times\vec{b}|=|\overrightarrow a||\overrightarrow b|\sin\theta$で表せるの。

2.1. 外積と平行四辺形の面積

ベクトル$\vec{a}$と$\vec{b}$の成分をそれぞれ$\vec{a} = (a_1, a_2, a_3)$、$\vec{b} = (b_1, b_2, b_3)$とします。外積の大きさは以下のようになる。

$|\vec{a}\times\vec{b}| = \sqrt{(a_2b_3 – a_3b_2)^2 + (a_3b_1 – a_1b_3)^2 + (a_1b_2 – a_2b_1)^2}$

ベクトルを用いた三角形の面積の方法を用いると、ベクトルによって張られる平行四辺形の面積を$T$、三角家の面積を$S$とすると、$T=2S$になる。面積$T$を求めると、

$$T=\sqrt{|\overrightarrow a|^2|\overrightarrow b|^2-(\overrightarrow a \cdot \overrightarrow b)^2}$$

$$=\sqrt{(a_1^2+a_2^2+a_3^2)(b_1^2+b_2^2+b_3^2)-(a_1b_1+a_2b_2+a_3b_3)^2}$$

$$=\sqrt{a_1^2b_1^2+a_1^2b_2^2+a_1^2b_3^2+a_2^2b_1^2+a_2^2b_2^2+a_2^2b_3^2+a_3^2b_1^2+a_3^2b_2^2+a_3^2b_3^2\\- a_1^2b_1^2 – 2a_1b_1a_2b_2 – 2a_1b_1a_3b_3 – a_2^2b_2^2 – 2a_2b_2a_3b_3 – a_3^2b_3^2}$$

$$=\sqrt{(a_1^2b_2^2-2a_1b_1a_2b_2+a_2^2b_1^2)+(a_1^2b_3^2- 2a_1b_1a_3b_3+a_3^2b_1^2)+(a_2^2b_3^2- 2a_2b_2a_3b_3+a_3^2b_2^2)}$$

$$=\sqrt{(a_1b_2 – a_2b_1)^2 + (a_1b_3 – a_3b_1)^2 + (a_2b_3 – a_3b_2)^2} $$

$$=|\vec{a}\times\vec{b}|$$

また、$S=\dfrac{1}{2}|\overrightarrow a||\overrightarrow b|\sin\theta$とあらわすことができるから、

$T=|\overrightarrow a||\overrightarrow b|\sin\theta$

となる。したがって、

$|\vec{a}\times\vec{b}|=|\overrightarrow a||\overrightarrow b|\sin\theta$

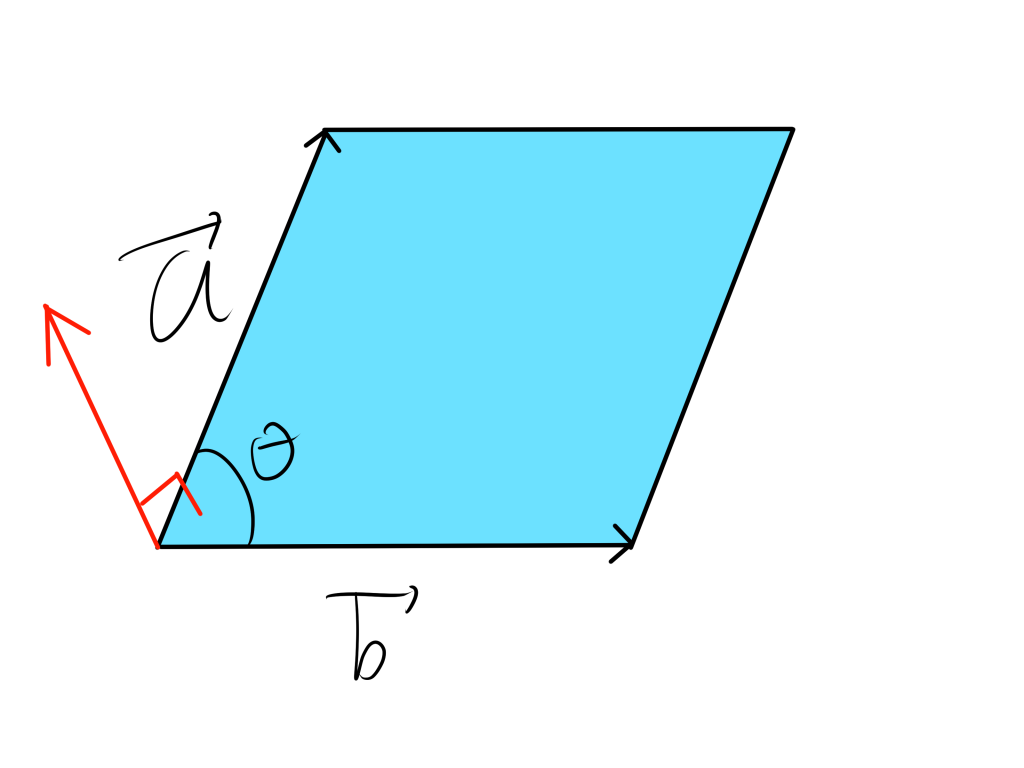
図であらわすと以下のようになります。