決定性有限オートマトン（DFA）と非決定性有限オートマトン（NFA）の意味と違いについて

1. オートマトンとは

オートマトンとは、自動的に動作する機械やシステムの数学的なモデルであり、英語では”automaton”（単数）または”automata”（複数）と呼ばれます。

2. 決定性有限オートマトン（DFA）

まず、DFAは何なのか？ということについて、数式をいきなり見ても混乱する可能性があるため図を用いて説明したいと思います。以下の画像のようなものがDFAです。

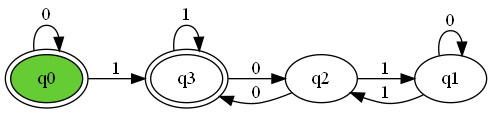
$q_{0}$からオートマトンは最初に遷移して、$q_{0}$と$q_{3}$の状態のときに文字列が終了したときに、文字列が受理されます。矢印方向の近くにある数字と同じ真野を受け取ったときに矢印の先の状態に移動します。次に、図のDFAにおける具体例を書きます。

2.1. DFAの例

文字列001001が与えられたとします。

最初に、0を受け取るため、状態$q_{0}$から$q_{0}$に遷移します。つまり、動きません。
次に、　0を受け取るため、状態$q_{0}$から$q_{0}$に遷移します。まだ、動きません。
次に、　1を受け取るため、状態$q_{0}$から$q_{3}$に遷移します。つまり、現在位置は$q_{3}$です。
次に、　0を受け取るため、状態$q_{3}$から$q_{2}$に遷移します。つまり、現在位置は$q_{2}$です。
次に、　0を受け取るため、状態$q_{2}$から$q_{3}$に遷移します。つまり、現在位置は$q_{3}$です。
最後に、1を受け取るため、状態$q_{3}$から$q_{3}$に遷移します。つまり、最終位置は$q_{3}$です。
したがって、$q_{0}$と$q_{3}$がオートマトンの受理状態であるから、001001は受理される。

このように、決定性有限オートマトン（DFA）は、入力として与えられた文字列を受け取り、あらかじめ決められた有限状態の集合の中で状態遷移を繰り返しながら処理を進め、最終的に入力された文字列が受理されるかどうかを判定するアルゴリズムです。

2.2. 数式的な表現

DFAを数式で表す場合、以下のように表現できます。DFAをMとする。

$M = (Q, Σ, δ, q_0, F)$

$Q$: 有限状態の集合
$Σ$: 入力記号列（有限個の文字からなる集合）
$δ$: 状態遷移関数。$Q × Σ → Q$（$×$は直積）の関数で、現在の状態と入力文字に対して、次の状態を一意に決定する。
$q_0$: 初期状態。$Q$の要素で、最初に遷移する状態を示す。
$F$: 受理状態の集合。$Q$の部分集合で、認識される文字列が終了した時に状態が含まれている場合、文字列が受理される。

上記の数式により、DFAを数学的に定義することができます。

3. 非決定性有限オートマトン（NFA）

DFAと同様に、まず、図を用いて説明させていただきます。

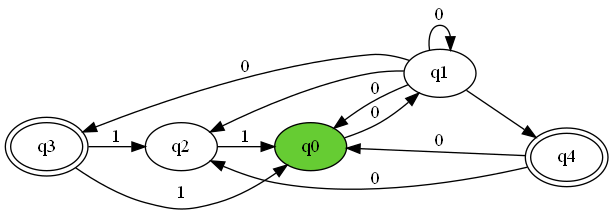
NFAの初期状態は、$q_{0}$で、受理状態は、$q_{3}$、$q_{4}$です。NFAの特徴として、$q_{1}$のように、複数の状態を遷移することができます。また、$q_{2}$と$q_{4}$への遷移は空動作と呼ばれ、入力なしで移動することができます。

3.1. NFAの例

文字列0が与えられたとする。
0を受け取るため、状態$q_{0}$から$\lbrace q_{1},q_{2},q_{4} \rbrace$に遷移します。なぜなら、$q_{1}$に移動した後、空動作で$q_{2}$と$q_{4}$に遷移するためである。
したがって、文字列0の遷移先の中に受理状態$q_{2}$が含まれているため、文字列0は受理される。

3.2. 数式的な表現

NFAを数式で表す場合、以下のように表現できます。NFAをMとする。

$M = (Q, Σ, δ, q_0, F)$

$Q$: 有限状態の集合
$Σ$: 入力記号列（有限個の文字からなる集合）
$δ$: 状態遷移関数。$Q × Σ → 2^Q$（$×$は直積、$2^Q$は冪集合）の関数で、現在の状態と入力文字に対して、次の状態が複数存在する。ただし、空動作付きのNFAの状態遷移関数は$Q × (Σ ∪ \lbrace ε \rbrace) → 2^Q$の関数となる。
$q_0$: 初期状態。$Q$の要素で、最初に遷移する状態を示す。
$F$: 受理状態の集合。$Q$の部分集合で、認識される文字列が終了した時に状態が含まれている場合、文字列が受理される。

上記の数式により、NFAを数学的に表現することができます。

4. DFAとNFAの違い

DFAとNFAの違いは以下の通りです。

4.1. 状態遷移の決定方法（状態遷移関数が異なる）

DFA：状態遷移が現在の状態と入力が一意（一対一）で決まっている。
NFA：状態遷移が現在の状態と入力だけでなく、複数の状態の集合に基づいて決定される。

4.2. 受理条件の判定方法

DFA：受理状態が事前に指定され、認識された文字列の最後の状態が受理状態である場合、その文字列を受理する。
NFA：受理条件が事前に指定されるが、認識された文字列の最後の状態が受理状態であるかどうかを確定するために、複数の可能性（集合）がある。

5. オートマトンに関するQ&A

5.1. Q1: オートマトンとは何ですか？

オートマトン（automaton）は、自動的に動作する機械やシステムの数学的モデルです。文字列の入力を受け取り、状態を遷移しながら処理を行い、特定のルールに従って受理・非受理を判定します。

5.2. Q2: 決定性有限オートマトン（DFA）とは何ですか？

DFA（Deterministic Finite Automaton）は、各状態において、ある入力文字に対する遷移先が一意に決まっている有限オートマトンです。

5.3. Q3: DFAはどのように動作しますか？

DFAは以下のように動作します：

1. 初期状態から開始する。
2. 入力文字を1文字ずつ受け取り、対応する状態に遷移する。
3. 文字列の最後に到達したとき、状態が受理状態にある場合、その文字列は受理される。

5.4. Q4: 非決定性有限オートマトン（NFA）とは何ですか？

NFA（Nondeterministic Finite Automaton）は、ある状態で1つの入力に対して複数の遷移先が存在する場合があるオートマトンです。また、空動作（ε遷移）と呼ばれる、入力なしでの遷移も可能です。

5.5. Q5: DFAとNFAの違いは何ですか？

DFAとNFAの主な違いは以下の通りです。

• 遷移の決定方法:
  • DFA: ある状態で受け取った入力ごとに遷移先が一意に決まる。
  • NFA: ある状態で受け取った入力に対して、複数の遷移先がある場合がある。

5.6. Q6: NFAはDFAに変換できますか？

はい、任意のNFAはDFAに変換可能です。この変換は「部分集合構成法（Subset Construction）」と呼ばれる方法を用いて行われます。