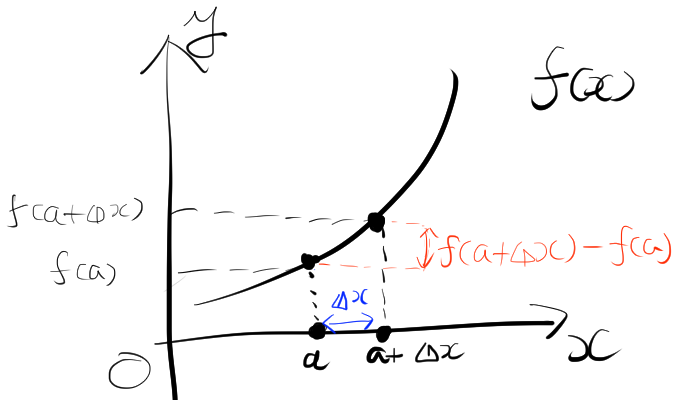
微分係数の定義・例題について

ふゅか

微分係数の定義って難しく感じる人も多いんじゃない？

はるか

そうかもね。でも、関数の変化を小さい範囲で見るだけ。簡単。

1. 微分係数

この式は、平均変化率（ある区間での関数の変化の割合）を \( \Delta x \) が限りなく小さくなるときに考えることで、微分係数を得ます。微分係数が存在する場合、関数 \( f(x) \) はその点 \( a \) で微分可能であるといい、 \( f'(a) \) はその点での接線の傾きを表します。

2. 微分係数を求める例題

ふゅか

実際に微分係数を求めてみよう！

2.1. 例題 1：$x^2$

微分係数の定義に基づいて、次のように計算します。 \[ f'(a) = \lim_{\Delta x \to 0} \frac{f(a + \Delta x) – f(a)}{\Delta x} \] ここで \( a = 3 \)、\( f(x) = x^2 \) です。

1. \( f(a + \Delta x) = (3 + \Delta x)^2 = 9 + 6\Delta x + (\Delta x)^2 \)
2. \( f(a) = 3^2 = 9 \)

これを定義に代入すると、

\[ f'(3) = \lim_{\Delta x \to 0} \frac{(9 + 6\Delta x + (\Delta x)^2) – 9}{\Delta x} \]

\[  = \lim_{\Delta x \to 0} \frac{6\Delta x + (\Delta x)^2}{\Delta x} \]

\[= \lim_{\Delta x \to 0} (6 + \Delta x) = 6 \]

したがって、\( f'(3) = 6 \) です。

2.2. 例題 2：$\sqrt{x}$

まず、微分係数の定義に従います。 \[ f'(a) = \lim_{\Delta x \to 0} \frac{f(a + \Delta x) – f(a)}{\Delta x} \] ここで \( a = 4 \)、\( f(x) = \sqrt{x} \) です。

1. \( f(a + \Delta x) = \sqrt{4 + \Delta x} \)
2. \( f(a) = \sqrt{4} = 2 \)

これを定義に代入すると、

\[ f'(4) = \lim_{\Delta x \to 0} \frac{\sqrt{4 + \Delta x} – 2}{\Delta x} \]

\[ = \lim_{\Delta x \to 0} \frac{\sqrt{4 + \Delta x} – 2}{\Delta x} \cdot \frac{\sqrt{4 + \Delta x} + 2}{\sqrt{4 + \Delta x} + 2} \]

\[  = \lim_{\Delta x \to 0} \frac{(4 + \Delta x) – 4}{\Delta x (\sqrt{4 + \Delta x} + 2)} \]

\[= \lim_{\Delta x \to 0} \frac{\Delta x}{\Delta x (\sqrt{4 + \Delta x} + 2)} \]

\[= \lim_{\Delta x \to 0} \frac{1}{\sqrt{4 + \Delta x} + 2} = \frac{1}{4} \]

したがって、\( f'(4) = \frac{1}{4} \) です。

2.3. 例題 3：$\sin(x)$

微分係数の定義に従います。 \[ f'(a) = \lim_{\Delta x \to 0} \frac{f(a + \Delta x) – f(a)}{\Delta x} \] ここで \( a = 0 \)、\( f(x) = \sin(x) \) です。

1. \( f(a + \Delta x) = \sin(0 + \Delta x) = \sin(\Delta x) \)
2. \( f(a) = \sin(0) = 0 \)

これを定義に代入すると、

\[ f'(0) = \lim_{\Delta x \to 0} \frac{\sin(\Delta x) – 0}{\Delta x} \]

\[ = \lim_{\Delta x \to 0} \frac{\sin(\Delta x)}{\Delta x} \]

有名な極限の結果から、 \[ \lim_{\Delta x \to 0} \frac{\sin(\Delta x)}{\Delta x} = 1 \]

したがって、\( f'(0) = 1 \) です。