点と直線の距離の導出・法線ベクトルについて

1. 点と直線の距離の公式

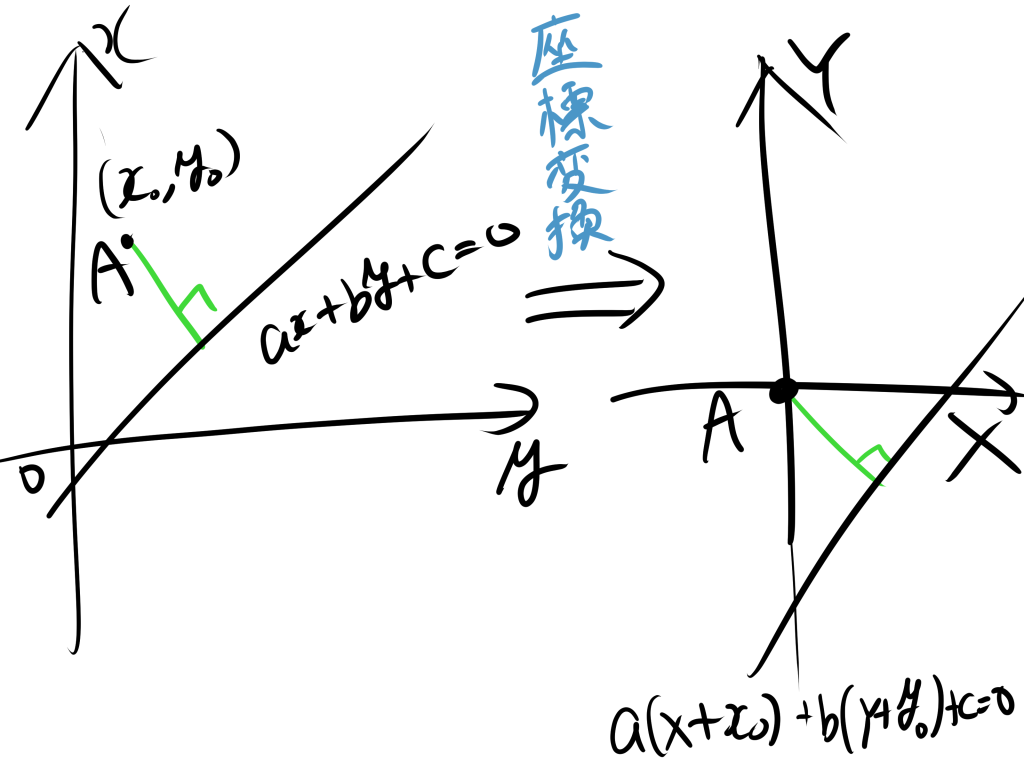
2. 座標をずらす証明

$[1]$　$a\neq0$であるとき

$ax+by+c=0$を直線lとする。

$xy$座標を$(x_0,y_0)$だけずらした座標系を$XY$座標とする。

$X=x-x_0,Y=y-y_0$となるから、$x=x_0+X,y=y_0+Y$より、直線の式に代入すると、

$$a(X+x_0)+b(Y+y_0)+c=0$$

となる。一方で、$X=x-x_0,Y=y-y_0$より、$XY$平面上で点$A$は$(0,0)$となる。点$A$を通り、$l$に垂直な直線は

$$Y=\dfrac{b}{a}X$$

となる。よって、交点$H$の座標を求めると

$$a(X+x_0)+b\left(\dfrac{b}{a}X+y_0\right)+c=0$$

$$X\left(a+\dfrac{b^2}{a}\right)=-c-by_0-ax_0$$

両辺を$a$倍すると、

$$X(a^2+b^2)=-a(c+by_0+ax_0)$$

$$X=\dfrac{-a(c+by_0+ax_0)}{a^2+b^2}$$

$$Y=\dfrac{-b(c+by_0+ax_0)}{a^2+b^2}$$

よって$AH$の長さは、

$$AH=\sqrt{\left(\dfrac{-a(c+by_0+ax_0)}{a^2+b^2}\right)^2+\left(\dfrac{-b(c+by_0+ax_0)}{a^2+b^2}\right)^2}$$

$$AH=\sqrt{\dfrac{a^2+b^2}{(a^2+b^2)^2}(c+by_0+ax_0)^2}$$

$$AH=\sqrt{\dfrac{1}{a^2+b^2}(c+by_0+ax_0)^2}$$

$$AH=\dfrac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}$$

よって、座標をずらしても長さは変わらないから、

$$d=\dfrac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}$$

となる。

[2]$a=0$であるとき

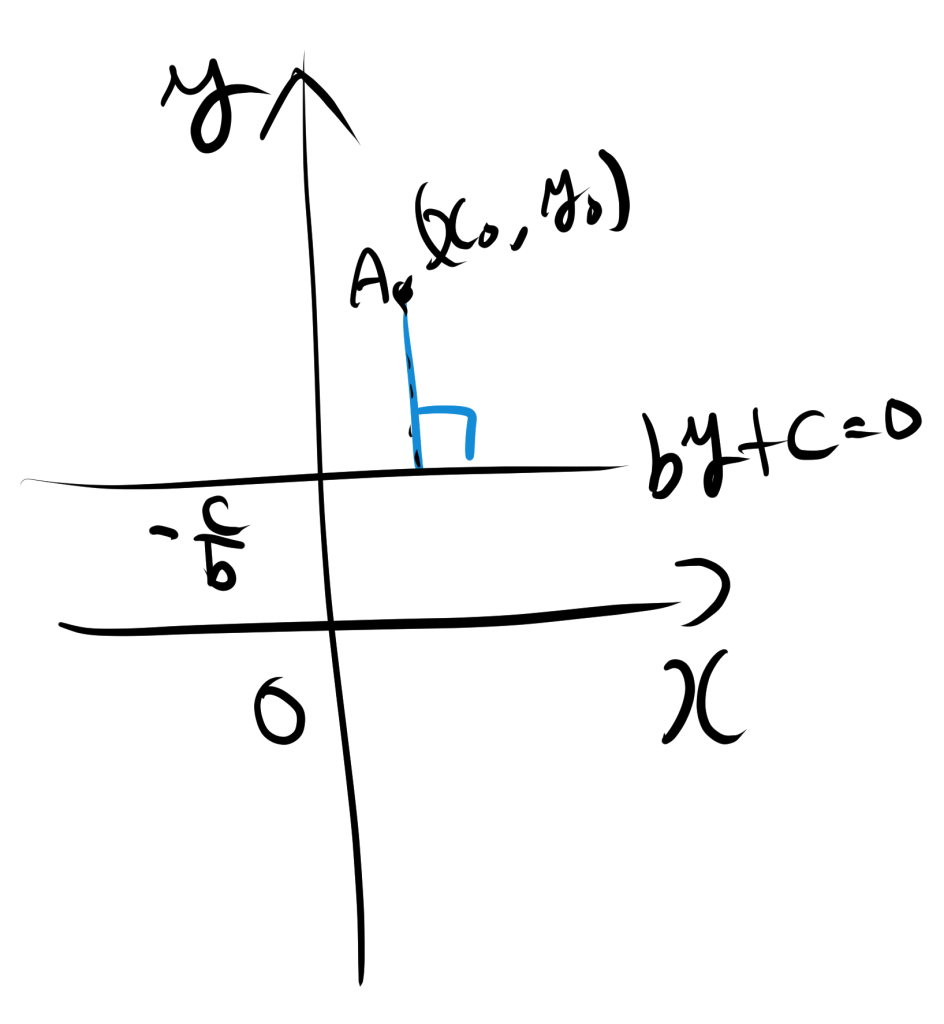
距離$d$は以下のようになる。

$$d=\left|y_0-(-\dfrac{c}{b})\right|$$

$$=\left|y_0+\dfrac{c}{b}\right|$$

$$=\left|\dfrac{by_0+c}{b}\right|$$

$$=\left|\dfrac{by_0+c}{b}\right|$$

これは、点$A$から、直線と距離の公式に代入したものと同じになるため、$a=0$のときも成り立つ。

3. ベクトルを用いた証明

3.1. 成分・内積の計算を行う

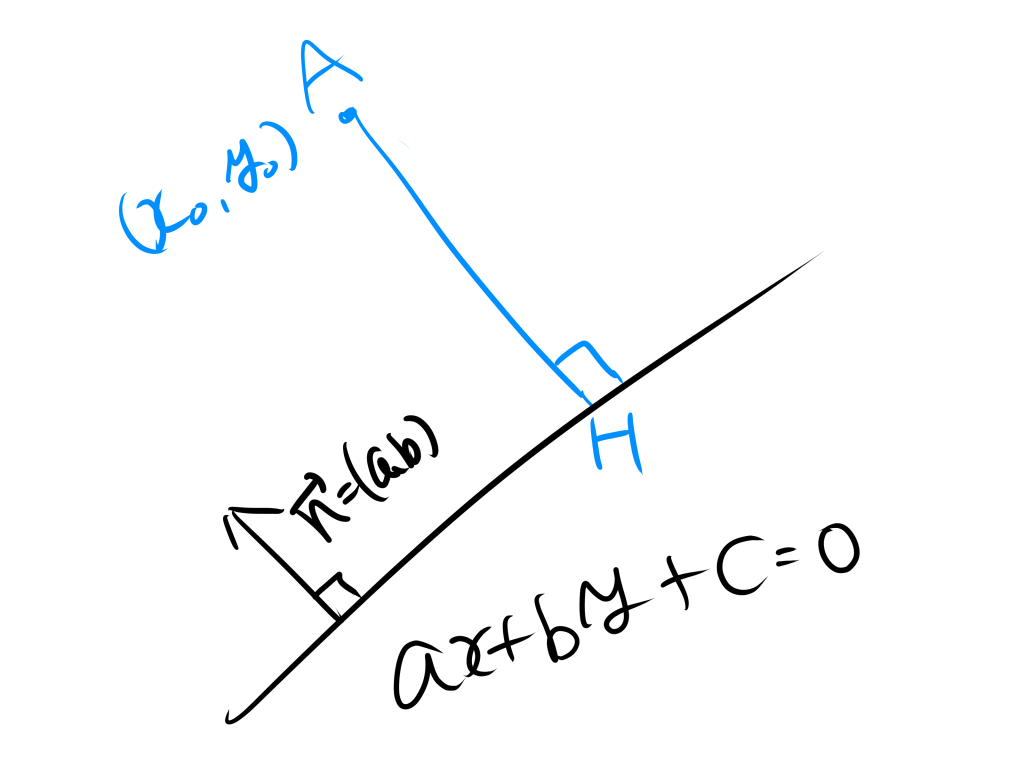
$ax+by+c=0$の法線ベクトルは$\vec{n}=(a,b)$となる。

$\vec{AH}$は$\vec{n}$に平行であるから、実数$k$を用いて表すと、

$$\vec{AH}=k\vec{n}$$

となる。$H$の座標を$(x_1,y_1)$とすると、

$$\vec{OH}=(x_1,y_1)$$

となるため、

$$\vec{OH}-\vec{OA}=k\vec{n}$$

$$\Leftrightarrow \begin{pmatrix}x_1-x_0\\y_1-y_0 \end{pmatrix}=k\begin{pmatrix}a\\b \end{pmatrix}$$

両辺に$\begin{pmatrix}a\\b \end{pmatrix}$の内積をとると、

$$\Leftrightarrow \begin{pmatrix}x_1-x_0\\y_1-y_0 \end{pmatrix}\cdot\begin{pmatrix}a\\b \end{pmatrix}=k\begin{pmatrix}a\\b \end{pmatrix}\cdot\begin{pmatrix}a\\b \end{pmatrix}$$

$$a(x_1-x_0)+b(y_1-y_0)=k(a^2+b^2)$$

$$\therefore k=\dfrac{a(x_1-x_0)+b(y_1-y_0)}{a^2+b^2}$$

点Hは直線$l$上の点に存在するため、$ax_1+by_1+c=0$となり、

$$k=\dfrac{-ax_0-by_0-c}{a^2+b^2}$$

したがって、距離$d$は

$$d=|k\vec n|$$

$$d=\left|\dfrac{-ax_0-by_0-c}{a^2+b^2}\sqrt{a^2+b^2}\right|$$

$$d=\dfrac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}$$

3.2. 直線の式に代入する

$$\begin{pmatrix}x_1-x_0\\y_1-y_0 \end{pmatrix}=k\begin{pmatrix}a\\b \end{pmatrix}$$

となることを先ほど示しましたが、これを変形します。

$$\begin{pmatrix}x_1\\y_1 \end{pmatrix}=\begin{pmatrix}x_0+ka\\y_0+kb \end{pmatrix}$$

また、$ax_1+by_1+c=0$に以上の結果を代入すると、

$$a(x_0+ka)+b(y_0+kb)+c=0$$

$$k(a^2+b^2)=-ax_0-by_0-c$$

$$k=\dfrac{-ax_0-by_0-c}{a^2+b^2}$$

となり、先ほどと同じ値が得られた。先ほどの証明と同じことを行えば、点と直線の距離の公式が証明できる。