内分点と外分点の座標と証明、例題について
1. 内分点とは
1.1. 内分点の座標の求め方
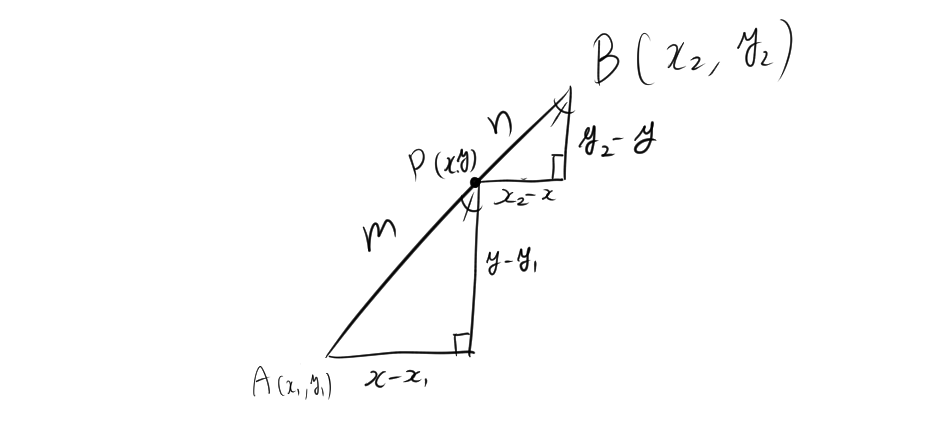
2次元平面で、点 \( A(x_1, y_1) \) と点 \( B(x_2, y_2) \) を結ぶ線分を \( m : n \) の比で内分する点 \( P \) の座標は次の式で求められます：
\[ P \left( \frac{nx_1 + mx_2}{m + n}, \frac{ny_1 + my_2}{m + n} \right) \]
この公式を使うことで、点 \( P \) が線分 \( AB \) の内部でどの位置にあるかを簡単に求めることができます。
1.2. 例題
点 \( A(2, 3) \) と点 \( B(8, 5) \) を \( 3 : 2 \) の比で内分する点 \( P \) の座標を求めてみましょう。
\[ P \left( \frac{2 \times 2 + 3 \times 8}{3 + 2}, \frac{2 \times 3 + 3 \times 5}{3 + 2} \right) \]
計算すると
\[ P \left( \frac{4 + 24}{5}, \frac{6 + 15}{5} \right) = P(\frac{28}{5}, \frac{21}{5}) \]
1.3. 内分点の座標の公式の導出
[1]まず、x座標を求めます。相似な三角形の性質から、
$$(x-x_1):(x_2-x)=m:n$$
与えられた式 を \(x\) について解きます。
\[ n (x – x_1) = m (x_2 – x) \]
計算すると、
$$\begin{align*} n x – n x_1 &= m x_2 – m x \\ n x + m x &= m x_2 + n x_1 \\ (n + m) x &= m x_2 + n x_1 \end{align*}$$
両辺を \((n + m)\) で割ります。
\[ x = \frac{m x_2 + n x_1}{n + m} \]
[2]次に、y座標を求めます。相似な三角形の性質から、
$$(y-y_1):(y_2-y)=m:n$$
与えられた式を \(y\) について解きます。
\[ n y – n y_1 = m y_2 – m y \]
\(y\) に関する項を左辺に集め、それ以外の項を右辺に移します。
\[ n y + m y = m y_2 + n y_1 \]
\[ (n + m) y = m y_2 + n y_1 \]
両辺を \((n + m)\) で割ります。
\[ y = \frac{m y_2 + n y_1}{n + m} \]
2. 外分点とは
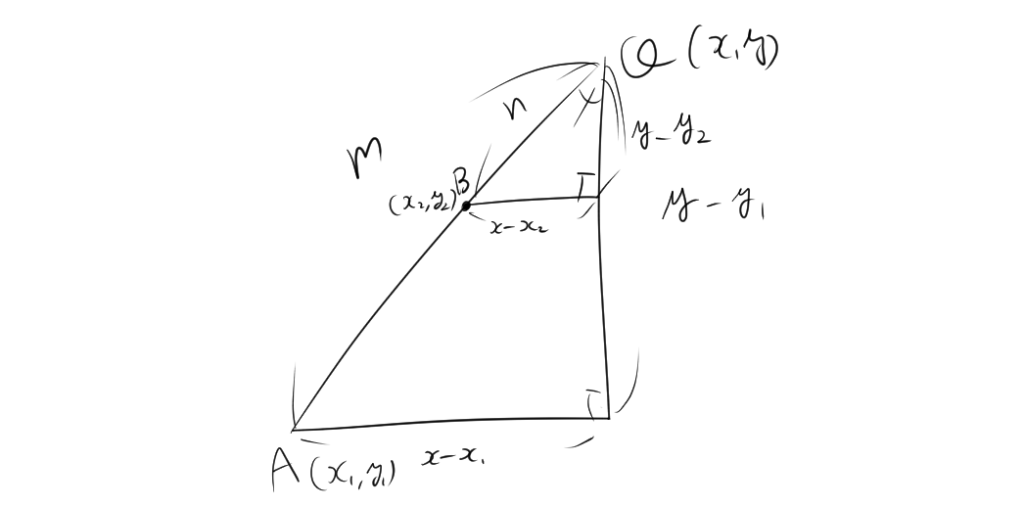
2.1. 外分点の座標の求め方
\[ Q \left( \frac{-nx_1 + mx_2}{m – n}, \frac{-ny_1 + my_2}{m – n} \right) \]
この公式は、点が線分の延長上にある場合の位置を示します。
2.2. 例題
点 \( A(1, 2) \) と点 \( B(5, 6) \) を \( 2 : 1 \) の比で外分する点 \( Q \) の座標を求めてみましょう。
\[ Q \left( \frac{-1 \times 1 + 2 \times 5}{2 – 1}, \frac{-1 \times 2 + 2 \times 6}{2 – 1} \right) \]
計算すると
\[ Q \left( \frac{-1 + 10}{1}, \frac{-2 + 12}{1} \right) = Q(9, 10) \]
よって、外分点 \( Q \) の座標は \( (9, 10) \) です。
2.3. 外分点の座標の公式の導出
[1]まず、x座標を求めます。相似な三角形の性質から、
$$(x-x_1):(x-x_2)=m:n$$
まず、与えられた方程式を展開します。
\[ n (x – x_1) = m (x – x_2) \]
\[ nx – nx_1 = mx – mx_2 \]
次に、\(x\) に関する項を左辺に、定数項を右辺に移項します。
\[ nx – mx = nx_1 – mx_2 \]
共通因数 \(x\) をくくり出します。
\[ (n – m)x = nx_1 – mx_2 \]
両辺を \((n – m)\) で割ります（ただし、\(n \neq m\) ）。
\[ x = \frac{nx_1 – mx_2}{n – m} \]
これが解となります。
[2]次に、y座標を求めます。相似な三角形の性質から、
$$(y-y_1):(y-y_2)=m:n$$
与えられた式を \(y\) について解きます。
\[ n y – n y_1 = m y – m y_2 \]
\[ n y -m y = n y_1-m y_2 \]
\[ (n – m) y = n y_1-m y_2 \]
両辺を \((n – m)\) で割ります（ただし、\(n \neq m\) ）。
\[ y = \frac{ n y_1-m y_2 }{n – m} \]
