約数の個数と約数の総和の証明、計算について

1. 約数とは
約数とは、ある整数を割り切ることができる整数のことを指します。
例えば、12 の約数は次の通りです。
\[ 12 \div 1 = 12, \quad 12 \div 2 = 6, \quad 12 \div 3 = 4, \quad 12 \div 4 = 3, \quad 12 \div 6 = 2, \quad 12 \div 12 = 1 \]
したがって、12 の約数は \( 1, 2, 3, 4, 6, 12 \) です。
2. 約数の個数
任意の正の整数 \( n \)を素因数分解すると
\[ n = p_1^{e_1} \cdot p_2^{e_2} \cdot \dots \cdot p_k^{e_k} \]
ここで、\( p_1, p_2, \dots, p_k \) は \( n \) の素因数で、\( e_1, e_2, \dots, e_k \) はそれぞれの素因数の指数です。
\[ d(n) = (e_1 + 1)(e_2 + 1) \cdots (e_k + 1) \]
つまり、各素因数の指数に 1 を足して、それらを掛け合わせたものが約数の個数になります。
2.1. 例
\( n = 60 \) の場合、60 を素因数分解すると
\[ 60 = 2^2 \cdot 3^1 \cdot 5^1 \]
よって、約数の個数は
\[ d(60) = (2 + 1)(1 + 1)(1 + 1) = 3 \cdot 2 \cdot 2 = 12 \]
60 の約数は 12 個あります。
実際に、60 の約数は次の通りです。
1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
2.2. 約数の個数の公式の証明
まず、\( n \) を素因数分解します。
\[ n = p_1^{e_1} \cdot p_2^{e_2} \cdot \dots \cdot p_k^{e_k} \]
このとき、\( n \) の約数は \( n \) の素因数分解の形を用いて次のように書けます。
\[ n の約数 = p_1^{a_1} \cdot p_2^{a_2} \cdot \dots \cdot p_k^{a_k} \]
ここで、\( a_1, a_2, \dots, a_k \) は、それぞれ次の範囲を取ります。
\[ 0 \leq a_1 \leq e_1,\quad 0 \leq a_2 \leq e_2, \quad \dots, \quad 0 \leq a_k \leq e_k \]
つまり、各素因数 \( p_i \) に対して、その指数 \( a_i \) は \( 0 \) から \( e_i \) までの整数を取ります。
したがって、\( p_1^{a_1} \cdot p_2^{a_2} \cdot \dots \cdot p_k^{a_k} \) の形で表される約数の個数は、\( a_1 \) の取り得る値が \( e_1 + 1 \) 通り、\( a_2 \) の取り得る値が \( e_2 + 1 \) 通り、…、\( a_k \) の取り得る値が \( e_k + 1 \) 通りです。すなわち、約数の個数は次のようになります。
\[ d(n) = (e_1 + 1)(e_2 + 1)\dots(e_k + 1) \]
これにより、約数の個数の公式が成り立つことが証明されました。
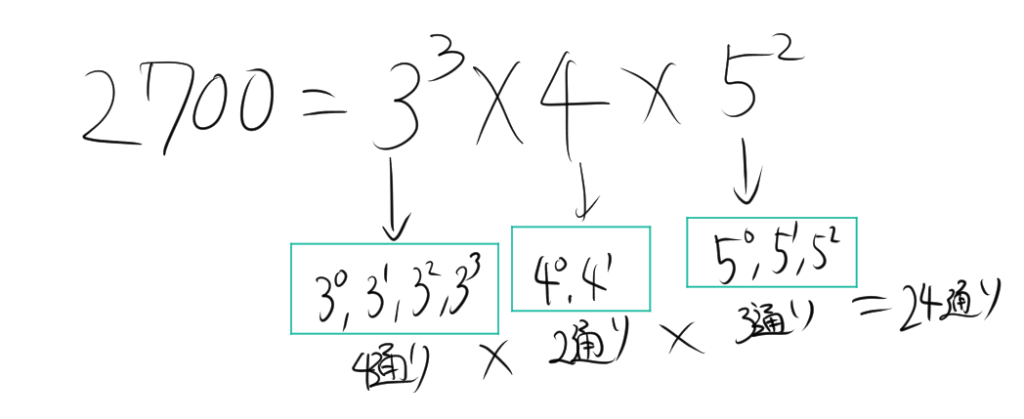
直感的なイメージは
3. 約数の総和
任意の正の整数 \( n \)を素因数分解すると
\[ n = p_1^{e_1} \cdot p_2^{e_2} \cdot \dots \cdot p_k^{e_k} \]
ここで、\( p_1, p_2, \dots, p_k \) は \( n \) の素因数で、\( e_1, e_2, \dots, e_k \) はそれぞれの素因数の指数です。
\[ \sigma(n) = (1 + p_1 + \dots + p_1^{e_1})(1 + p_2 + \dots + p_2^{e_2}) \cdots (1 + p_k + p_k^2 + \dots + p_k^{e_k}) \]
また、積の記号$\displaystyle \prod$を利用することで、次のように表すことができます。
\[ \sigma(n) = \prod_{i=1}^{k} \frac{p_i^{e_i + 1} – 1}{p_i – 1} = \prod_{i=1}^{k} (1+p_i+p_i^2+\cdots + p_i^{e_i})\]
3.1. 例
\( n = 60 \) の場合、60 を素因数分解すると
\[ 60 = 2^2 \cdot 3^1 \cdot 5^1 \]
したがって、$\sigma(60)$は
\[ \sigma(60) = (1 + 2 + 2^2)(1 + 3)(1 + 5) = (1 + 2 + 4)(1 + 3)(1 + 5) = 7 \cdot 4 \cdot 6 = 168 \]
したがって、60 の約数の総和は 168 です。
実際に計算すると、
1 + 2 + 3 + 4 + 5 + 6 + 10 + 12 + 15 + 20 + 30 + 60 = 168
3.2. 約数の総和の公式の証明
\( n \) が次のように素因数分解できるとします。
\[ n = p_1^{e_1} \cdot p_2^{e_2} \cdot \dots \cdot p_k^{e_k} \]
\( n \) の全ての約数は次の形で表されます。
\[ n の約数 = p_1^{a_1} \cdot p_2^{a_2} \cdot \dots \cdot p_k^{a_k} \]
ここで、\( a_1, a_2, \dots, a_k \) は、前述の通り、各素因数に対して \( 0 \leq a_i \leq e_i \) という条件を満たします。よって、約数の総和 \( \sigma(n) \) は次のように書けます。
\[ \sigma(n) = \sum_{a_1=0}^{e_1} \sum_{a_2=0}^{e_2} \dots \sum_{a_k=0}^{e_k} p_1^{a_1} p_2^{a_2} \dots p_k^{a_k} \]
この式は積の形に変形できます。
\[ \sigma(n) = \left( \sum_{a_1=0}^{e_1} p_1^{a_1} \right) \left( \sum_{a_2=0}^{e_2} p_2^{a_2} \right) \dots \left( \sum_{a_k=0}^{e_k} p_k^{a_k} \right) \]
各素因数に対する部分和 \( \displaystyle\sum_{a_i=0}^{e_i} p_i^{a_i} \) は等比数列の和の形になるので、
\[ \sum_{a_i=0}^{e_i} p_i^{a_i} = \frac{p_i^{e_i + 1} – 1}{p_i – 1} \]
したがって、約数の総和 \( \sigma(n) \) は次のように書けます。
\[ \sigma(n) = \prod_{i=1}^{k} \frac{p_i^{e_i + 1} – 1}{p_i – 1} = \prod_{i=1}^{k} (1+p_i+p_i^2+\cdots + p_i^{e_i})\]
$\displaystyle \prod$は積を表す記号です。