【図解】ド・モアブルの定理の証明と負の場合について

1. ド・モアブルの定理

1.1. 対応関係図

ド・モアブルの定理を数式で色分けすると以下のようになります。

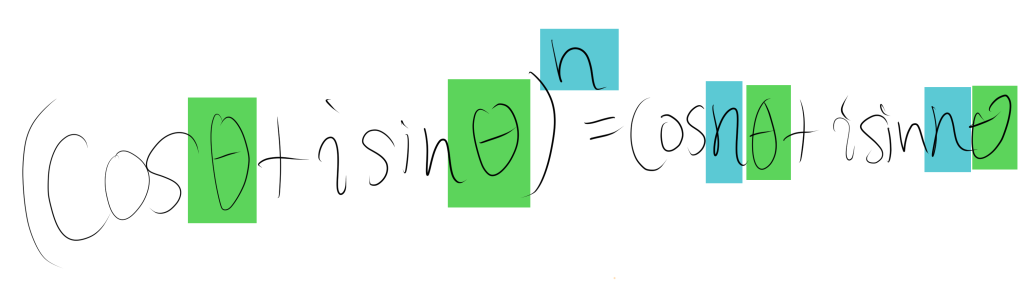
1.2. 数学的帰納法による証明

数学的帰納法を利用して証明する。

$n=0$のとき、

$$(\cos\theta+i\sin\theta)^0=1$$

$$\cos 0 +i \sin 0=1$$

したがって、n=0の時成り立つ。

$n=k$のとき、

$$(\cos\theta+i\sin\theta)^k=\cos k\theta +i \sin k \theta$$

を満たすと仮定する。

$n=k+1$のとき、

$$(\cos\theta+i\sin\theta)^{k+1}-\cos (k+1)\theta -i \sin (k+1) \theta$$

$$=(\cos\theta+i\sin\theta)(\cos k\theta+i\sin k\theta)-\cos(k+1)\theta – i\sin(k+1)\theta$$

加法定理より、

$$=\cos k\theta\cos\theta -\sin k\theta\sin\theta +i(\sin k\theta+\sin\theta\cos k\theta)  -(\cos k\theta \cos \theta -\sin k\theta\sin\theta )-i(\sin k\theta \cos\theta+\sin\theta\cos k\theta)$$

$$=0$$

$$\therefore (\cos\theta+i\sin\theta)^{k+1}=\cos (k+1)\theta +i \sin (k+1) \theta$$

したがって、$n=k+1$の時も成り立つ。

数学的帰納法により、$n \geq 0$のとき、

$(\cos\theta+i\sin\theta)^n=\cos n\theta +i \sin n \theta$

が成り立つ。

1.3. オイラーの公式による確認

オイラーの公式 $e^{i\theta}=\cos\theta+i\sin\theta$より、

$$(\cos\theta+i\sin\theta)^n$$

$$=(e^{i\theta})^n$$

$$=e^{in\theta}$$

$$=\cos n\theta +i \sin n \theta$$

$$\therefore(\cos\theta+i\sin\theta)^n=\cos n\theta +i \sin n\theta$$

2. マイナスのとき

ド・モアブルの定理は実はマイナスのときも成り立ちます。2通りの証明方法で示したいと思います。

2.1. n<0とするときの証明

$n<0$であるとすると、

$$(\cos\theta + i \sin\theta)^{n}=\dfrac{1}{(\cos\theta+i\sin\theta)^{-n}}$$

$-n>0$より、ド・モアブルの定理が成り立つため、

$$=\dfrac{1}{(\cos\theta+i\sin\theta)^{-n}}$$

$$=\dfrac{1}{\cos(-n)\theta+i\sin(-n)\theta}$$

分子分母に$\cos(-n)\theta-i\sin(-n)\theta$をかけると、

$$=\dfrac{\cos(-n)\theta-i\sin(-n)\theta}{(\cos(-n)\theta+i\sin(-n)\theta)(\cos(-n)\theta-i\sin(-n)\theta)}$$

$$=\dfrac{\cos(-n)\theta-i\sin(-n)\theta}{\cos^2(-n)\theta+\sin^2(-n)\theta}$$

$$=\cos(-n)\theta-i\sin(-n)\theta$$

$\cos n\theta=\cos (-n)\theta$、$\sin n\theta=-\sin (-n)\theta$となるから、

$$=\cos(-n)\theta-i\sin(-n)\theta$$

$$=\cos n\theta+i\sin n\theta$$

となる。よって、n<0のときも、ド・モアブルの定理は成り立つ。

2.2. n>0とするときの証明

$-n<0$であるとすると、

$$(\cos\theta + i \sin\theta)^{-n}=\dfrac{1}{(\cos\theta+i\sin\theta)^{n}}$$

$n>0$より、ド・モアブルの定理が成り立つため、

$$=\dfrac{1}{(\cos\theta+i\sin\theta)^{n}}$$

$$=\dfrac{1}{\cos n\theta+i\sin n\theta}$$

分子分母に$\cos n\theta-i\sin n \theta$をかけると、

$$=\dfrac{\cos n\theta-i\sin n \theta}{(\cos n\theta+i\sin n\theta)(\cos n\theta-i\sin n \theta}$$

$$=\dfrac{\cos n\theta-i\sin n \theta}{\cos^2 n \theta+\sin^2 n \theta}$$

$$=\cos n\theta-i\sin n \theta$$

$\cos n\theta=\cos (-n)\theta$、$\sin n\theta=-\sin (-n)\theta$となるから、

$$=\cos(-n)\theta+i\sin(-n)\theta$$

となる。よって、

$$(\cos n \theta+i\sin n \theta)^{-n}=\cos(-n)\theta+i\sin(-n)\theta$$

となり、ド・モアブルの定理は成り立つ。