【図解】三角比の相互関係とその証明

1. 三角比の相互関係

2. $ \tan{\theta} = \dfrac{\sin\theta}{\cos{\theta}} $の証明

三角形を用いた証明を行います。

図より$x=r\cos\theta,y=r\sin\theta$と置いたとき、$\tan\theta=\dfrac{y}{x}$であるから、

$\tan\theta=\dfrac{y}{x}$

$=\dfrac{r\sin\theta}{r\cos\theta}$

$=\dfrac{\sin\theta}{\cos\theta}$

となる。

3. $ \sin^2{\theta} + \cos^2{\theta} = 1 $の証明

3.1. 三角形を用いた証明

図より$x=r\cos\theta,y=r\sin\theta$と置いたとき、三平方の定理より、

$x^2+y^2=r^2$

$r^2\cos^2\theta+r^2\sin^2\theta=r^2$

両辺を$r^2>0$で割ると、

$ \sin^2{\theta} + \cos^2{\theta} = 1 $

となる。

3.2. 円を用いた証明

三角形を用いた証明では$\theta$が鋭角$\left(0 < \theta <\dfrac{\pi}{2}\right)$しか証明できていないため、円を用いて証明する。

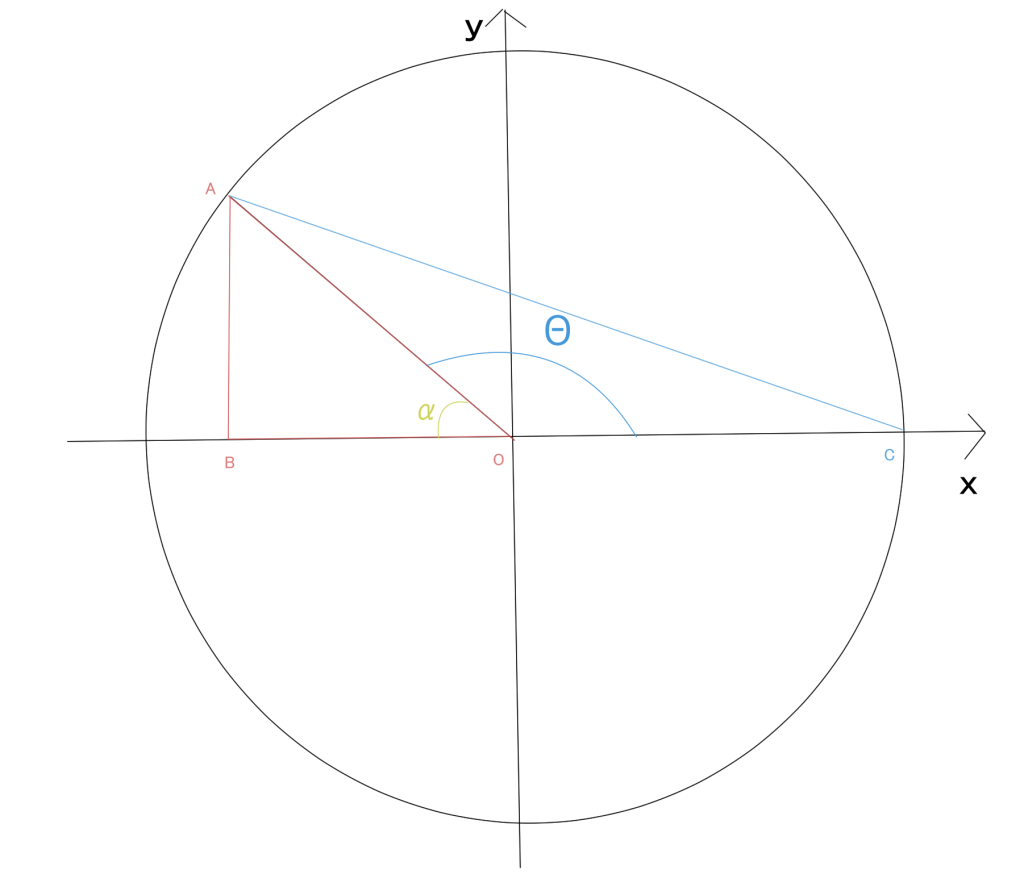
半径がrであるとき、点Aの座標は$\left(r\cos\theta,r\sin\theta\right)$となる。よって、半径がrであるから、$OA=r、AB=r|\cos\theta|、OB=r|\sin\theta|$より、三平方の定理を用いると、

$AB^2+OB^2=AO^2$

$r^2\cos^2\theta+r^2\sin^2\theta=r^2$

両辺を$r^2>0$で割ると、

$ \sin^2{\theta} + \cos^2{\theta} = 1 $

4. $1+\tan^2\theta=\dfrac{1}{\cos^2\theta}$の証明

$ \sin^2{\theta} + \cos^2{\theta} = 1 $を用いて証明を行います。

$\cos\theta\neq0$であるとき、$ \sin^2{\theta} + \cos^2{\theta} = 1 $の両辺を $\cos^2{\theta}$で割ると、

$1+\dfrac{\sin^2\theta}{\cos^2\theta}=\dfrac{1}{\cos^2\theta}$

$\tan\theta=\dfrac{\sin\theta}{\cos\theta}$であるから、

$1+\tan^2\theta=\dfrac{1}{\cos^2\theta}$