固有値・固有空間・固有ベクトルの計算方法や具体例について

1. 固有値とは

零ベクトルでない$n$次のベクトル$\boldsymbol x$が存在するとき、$\lambda$を$A$の固有値、$A$の固有ベクトルという。固有ベクトル$\boldsymbol x$は、行列$ A $によって線形変換された後も、方向が変わらない特別なベクトルです。固有値$\boldsymbol x$は、スカラー値となります。図にまとめると以下のようになります。

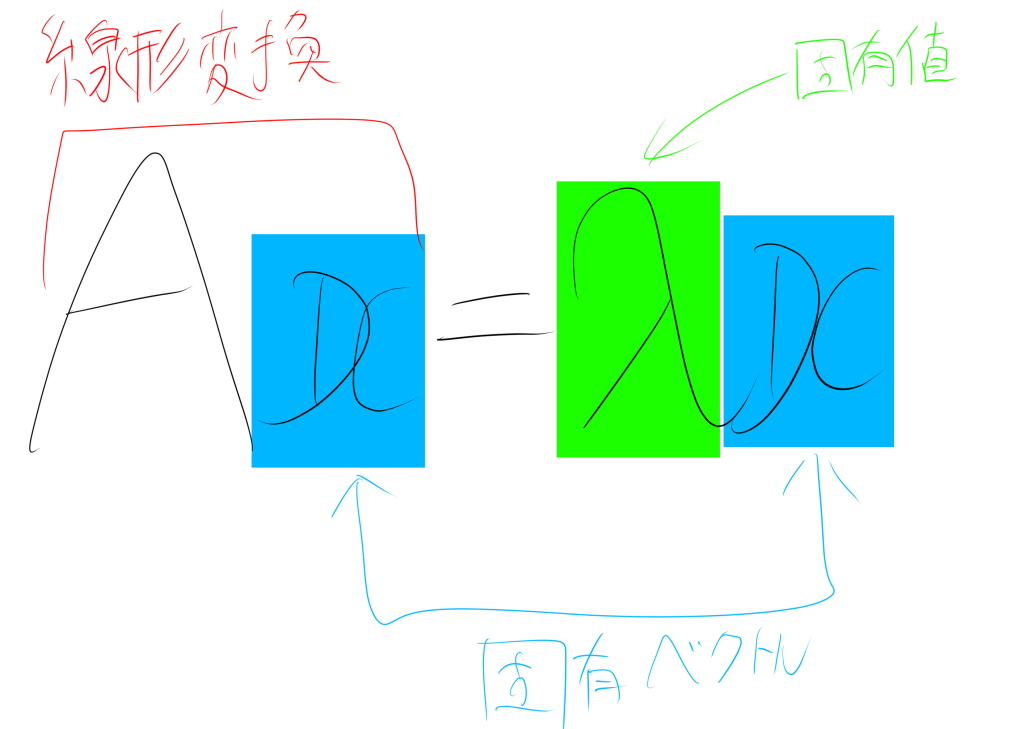
2. 固有値の計算

$A\boldsymbol x=\lambda \boldsymbol x$を変形する。

$A\boldsymbol x-\lambda \boldsymbol x=\boldsymbol{0}$

$(A-\lambda E)\boldsymbol x=\boldsymbol{0}$

$\boldsymbol x \neq \boldsymbol{0}$である。仮に$(A-\lambda E)$が正則（逆行列が存在する）であると仮定すると、

$\boldsymbol x=(A-\lambda E)^{-1}\boldsymbol{0}=\boldsymbol{0}$

となるため、$\boldsymbol x \neq \boldsymbol{0}$に矛盾している。

そのため、$(A-\lambda E)$が正則でない。

したがって、行列$(A-\lambda E)$が正則でない条件は、$\mathrm{det}(A-\lambda E)=0$となる。

$\mathrm{det}(A-\lambda E)=0$は固有方程式と呼ばれる。

3. 固有ベクトルと固有空間

固有値を計算した後、それぞれの固有値の場合にわけて、連立方程式で固有値を求めることができる。

4. 固有値の計算の例題

$\mathrm{det}(A-\lambda E)=0$より、

$\begin{vmatrix} 1-\lambda & 2 \\ 2 & 1-\lambda \\ \end{vmatrix}=0$

$(\lambda-1)^2-4=0$

$(\lambda-1-2)(\lambda-1+2)=0$

$(\lambda-3)(\lambda+1)=0$

$\lambda=3,-1$となる。

次に、固有ベクトルを求める。固有ベクトルを$\begin{bmatrix}x\\y \end{bmatrix}$とする。

$\lambda=3$であるとき、

$\begin{bmatrix} -2 & 2\\ 2 &-2 \\ \end{bmatrix}\begin{bmatrix}x\\y \end{bmatrix}=\boldsymbol{0}$

連立方程式の係数行列の階数を求めると、$\mathrm{rank}\begin{bmatrix} -2 & 2\\ 2 &-2 \\ \end{bmatrix}=1$となるため、解の自由度は1である。したがって、$s\neq0$を満たす任意定数を用いて、$x=s$と置くと、$y=s$となる。よって、固有ベクトルは、

$\begin{bmatrix}x\\y \end{bmatrix}=s\begin{bmatrix}1\\1 \end{bmatrix}$

固有空間は、

$V(3) = \left\langle \ \begin{bmatrix} 1\\1 \end{bmatrix} \ \right\rangle$

となる。

$\lambda=-1$であるとき、

$\begin{bmatrix} 2 & 2\\ 2 &2 \\ \end{bmatrix}\begin{bmatrix}x\\y \end{bmatrix}=\boldsymbol{0}$

連立方程式の係数行列の階数を求めると、$\mathrm{rank}\begin{bmatrix} 2 & 2\\ 2 &2 \\ \end{bmatrix}=1$となるため、解の自由度は1である。したがって、$s\neq0$を満たす任意定数を用いて、$x=s$と置くと、$y=-s$となる。よって、固有ベクトルは、

$\begin{bmatrix}x\\y \end{bmatrix}=s\begin{bmatrix}1\\-1 \end{bmatrix}$

固有空間は、

$V(-1) = \left\langle \ \begin{bmatrix} 1\\-1 \end{bmatrix} \ \right\rangle$

となる。