楕円の方程式の導出・性質・アニメーションについて

1. 楕円とは
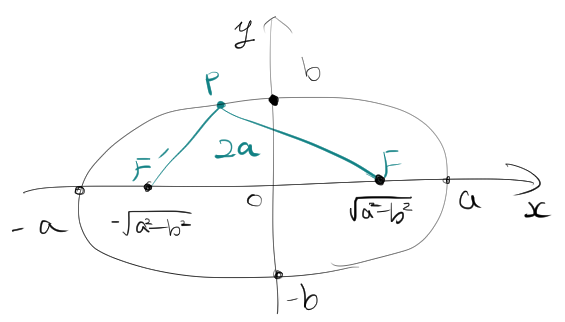
楕円は、2つの固定された点 \( F_1 \) と \( F_2 \)(これを焦点と呼びます)からの距離の和が一定である点の集合です。任意の点 \( P \) が焦点 \( F_1 \) および \( F_2 \) からの距離の和を \( 2a \) とすると、楕円の形状が次の式で定義されます。
\[ PF_1 + PF_2 = 2a \]
ここで、\( a \) は楕円の長軸の半分の長さです。
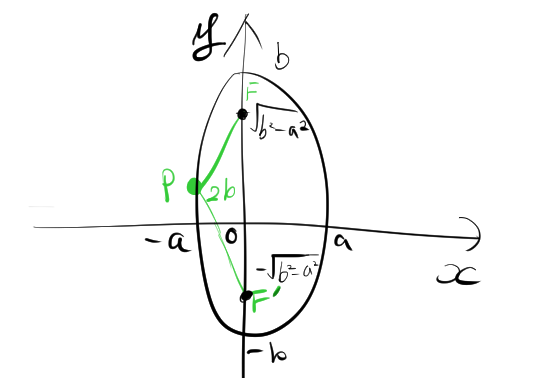
縦に長い楕円の場合は、2aではなく2bになります。
1.1. アニメーション
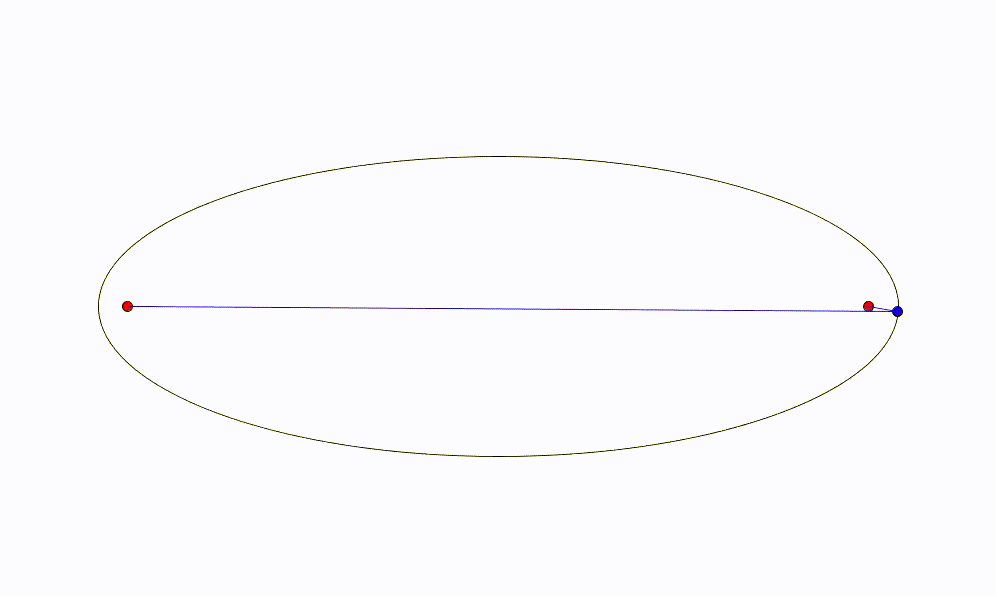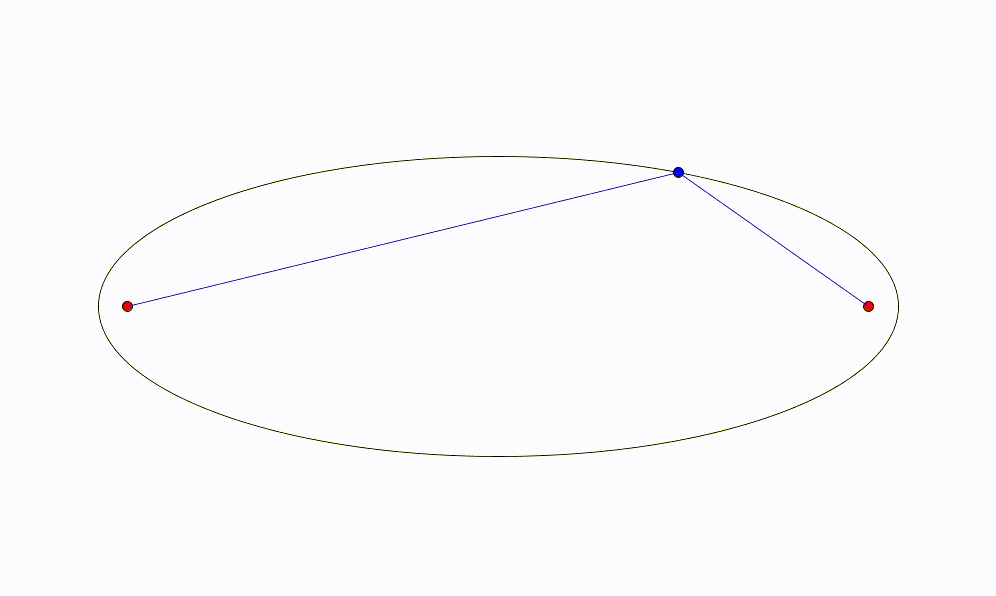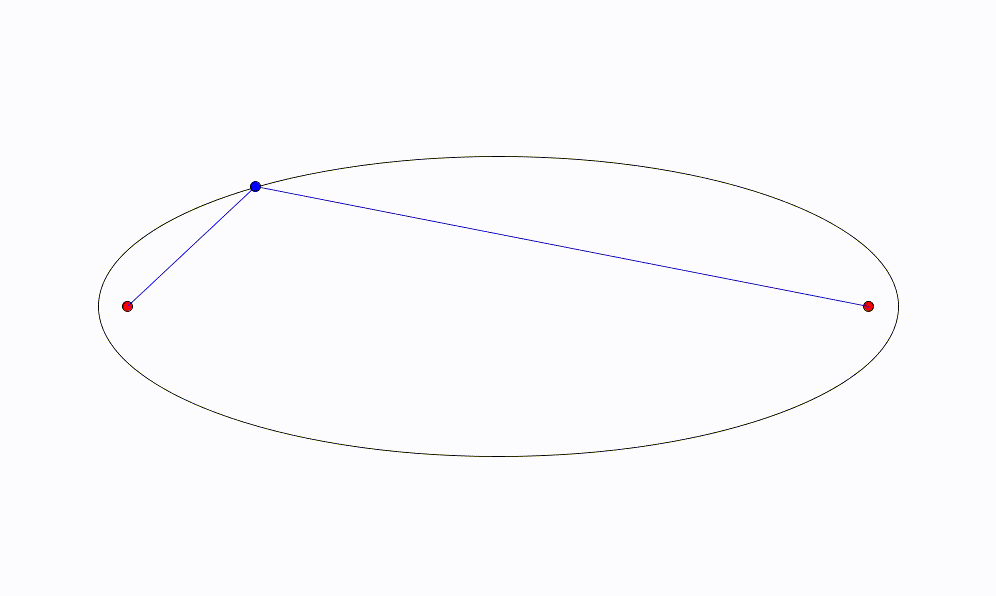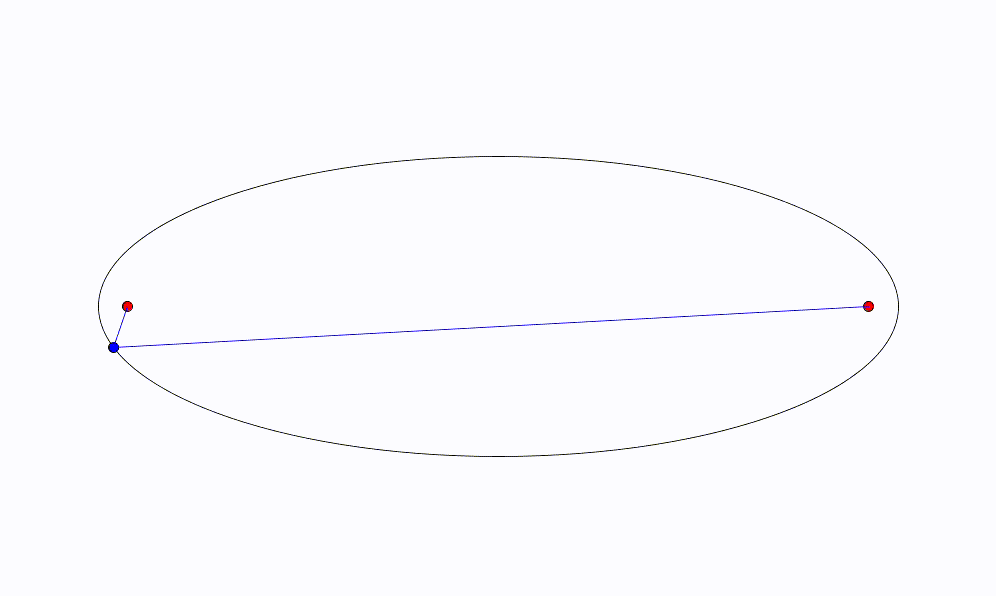
距離の和が一定であることをアニメーションで表すと次のようになる。
2. 楕円の方程式
\[ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \]
ここで、\( a > b \) であれば、楕円は横に広がった形になり、\( a < b \) であれば縦に広がった形になります。
2.1. a > bのときの、楕円の方程式の導出
楕円の定義から、焦点 \( F \) と \( F’ \) から任意の点 \( P(x, y) \) までの距離の和 \( PF+ PF’ = 2a \) を使って、楕円の方程式を導出します。
楕円の焦点を \( F(-c, 0) \) と \( F'(c, 0) \) とします(楕円が \( x \)-軸上に対称に配置されている場合)。$c=\sqrt{a^2-b^2}$と置きます。任意の点 \( P(x, y) \) が楕円上にあるとします。楕円の長軸の長さは \( 2a \)、短軸の長さは \( 2b \)です。
次の関係を満たします。
\[ PF+ PF’ = 2a \]
これを数式で表すと、次のようになります。
\[ \sqrt{(x + c)^2 + y^2} + \sqrt{(x – c)^2 + y^2} = 2a \]
まず、両辺から \( \sqrt{(x + c)^2 + y^2} \) を片方に移し、平方します。
\[ \sqrt{(x – c)^2 + y^2} = 2a – \sqrt{(x + c)^2 + y^2} \]
両辺を2乗して、次のようになります。
\[ (x – c)^2 + y^2 = \left( 2a – \sqrt{(x + c)^2 + y^2} \right)^2 \]
\[ (x – c)^2 + y^2 = 4a^2 – 4a\sqrt{(x + c)^2 + y^2} + (x + c)^2 + y^2 \]
ここで、両辺の共通項 を消去すると次のようになります。
$$-4cx-4a^2 = -4a\sqrt{(x+c)^2+y^2}$$
$$cx+a^2 = a\sqrt{(x+c)^2+y^2}$$
両辺をもう一度2乗すると次のようになる。
$$(cx+a^2 )^2= a^2(x+c)^2+a^2y^2$$
$c^2 = a^2-b^2$より、
$$(a^2-b^2)x^2+2ca^2x+a^4= a^2x^2+2ca^2x+a^2c^2+a^2y^2$$
$$-b^2x^2-a^2y^2= a^2(a^2-b^2)-a^4$$
$$-b^2x^2-a^2y^2 = -a^2b^2$$
$$\frac{x^2}{a^2}+\frac{y^2}{b^2} = 1$$
楕円の方程式は得られました。
この式は、中心が原点にあり、長軸が \( x \)軸に沿った楕円を表しています。
2.2. b > a のときの、楕円の方程式の導出
楕円の定義から、焦点 \( F \) と \( F’ \) から任意の点 \( P(x, y) \) までの距離の和 \( PF+ PF’ = 2b \) を使って、楕円の方程式を導出します。
焦点を \( F(-c, 0) \) と \( F'(c, 0) \) とし、\( c = \sqrt{b^2 – a^2} \) とします。任意の点 \( P(x, y) \) が楕円上にあると仮定します。楕円の長軸の長さは \( 2b \)、短軸の長さは \( 2a \) です。
次の関係が成り立ちます。
\[ PF+ PF’ = 2b \]
これを数式で表すと、次のようになります。
\[ \sqrt{(x + c)^2 + y^2} + \sqrt{(x – c)^2 + y^2} = 2b \]
まず、片方の平方根を移動させ、平方します。
\[ \sqrt{(x – c)^2 + y^2} = 2b – \sqrt{(x + c)^2 + y^2} \]
両辺を2乗すると、次の式が得られます。
\[ (x – c)^2 + y^2 = \left( 2b – \sqrt{(x + c)^2 + y^2} \right)^2 \]
\[ (x – c)^2 + y^2 = 4b^2 – 4b\sqrt{(x + c)^2 + y^2} + (x + c)^2 + y^2 \]
共通項を消去すると次のようになります。
$$-4cx – 4b^2 = -4b \sqrt{(x + c)^2 + y^2}$$
$$cx + b^2 = b \sqrt{(x + c)^2 + y^2}$$
もう一度2乗すると次の式が得られます。
$$(cx + b^2)^2 = b^2(x + c)^2 + b^2 y^2$$
\( c^2 = b^2 – a^2 \) より、
\[ (b^2 – a^2)x^2 + 2b^2cx + b^4 = b^2x^2 + 2b^2cx + b^2c^2 + b^2y^2 \]
\[ -a^2x^2 – b^2y^2 = b^2(b^2 – a^2) – b^4 \]
\[ -a^2x^2 – b^2y^2 = -a^2b^2 \]
最終的に、次の方程式が得られます。
\[ \frac{x^2}{b^2} + \frac{y^2}{a^2} = 1 \]
これが、中心が原点にあり、長軸が \( y \)軸に沿った楕円の方程式です。
3. 楕円の性質
3.1. 焦点と離心率
\[ e = \frac{c}{a} \]
3.2. 楕円の媒介変数表示
\[ x = a \cos \theta \]
\[ y = b \sin \theta \]
ここで、 \( 0 \leq \theta < 2\pi \) の範囲で動きます。
楕円の方程式は次のように表されます。
\[ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \]
ここで、\( x = a \cos \theta \) と \( y = b \sin \theta \) を代入します。すると、以下のように変形されます。
\[ \frac{(a \cos \theta)^2}{a^2} + \frac{(b \sin \theta)^2}{b^2} = 1 \]
\[ \frac{a^2 \cos^2 \theta}{a^2} + \frac{b^2 \sin^2 \theta}{b^2} = 1 \]
\[ \cos^2 \theta + \sin^2 \theta = 1 \]
この結果、左辺が 1 になるため、楕円の媒介変数表示は楕円の方程式を満たしていることが確認されます。
例えば、長半径が 5、短半径が 3 の楕円の場合、
\[ x = 5 \cos \theta \]
\[ y = 3 \sin \theta \]
このように表すことで、楕円の各点が角度 \( \theta \) に基づいて計算されます。