エピサイクロイド曲線の媒介変数表示・導出・アニメーションについて

はるか

エピサイクロイドって、円が転がるときにできる曲線。

ふゅか

そう！固定された円の外側をもう一つの円が転がると、その外周上の点が描く軌跡ね。見た目も面白いよね♪

はるか

媒介変数表示を使って、簡単に説明できる。

1. エピサイクロイド曲線とは

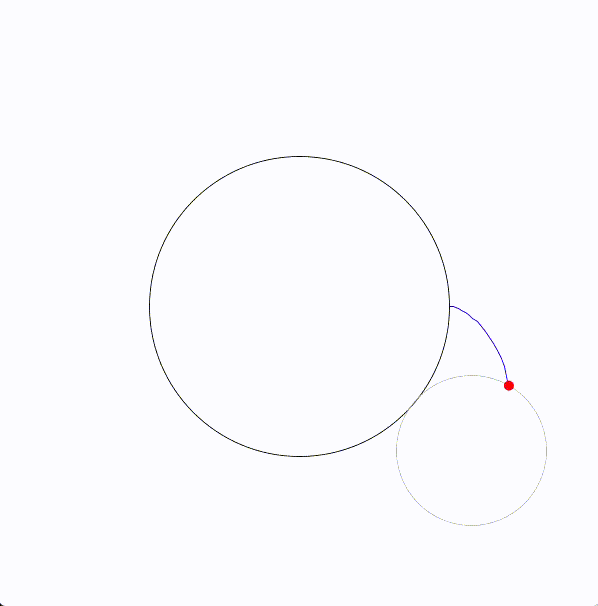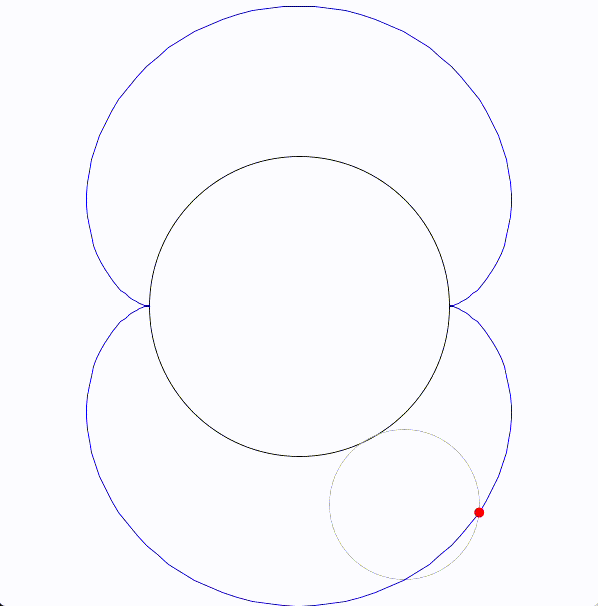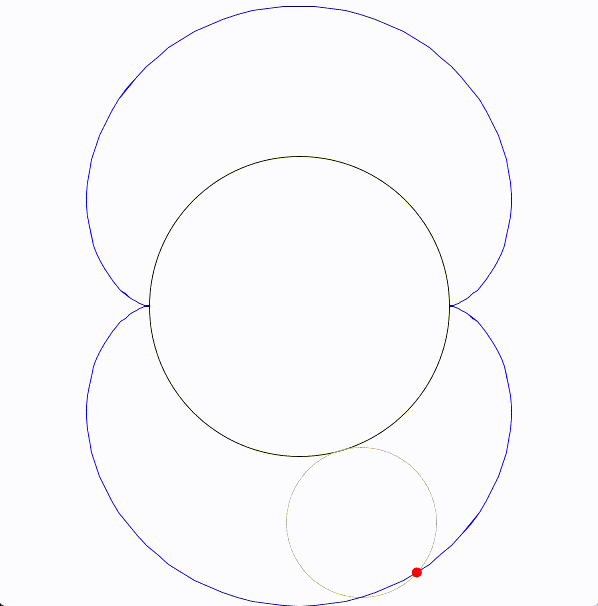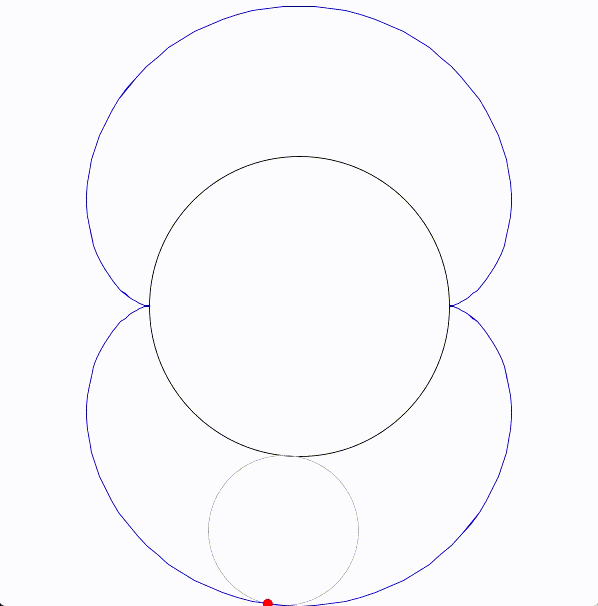
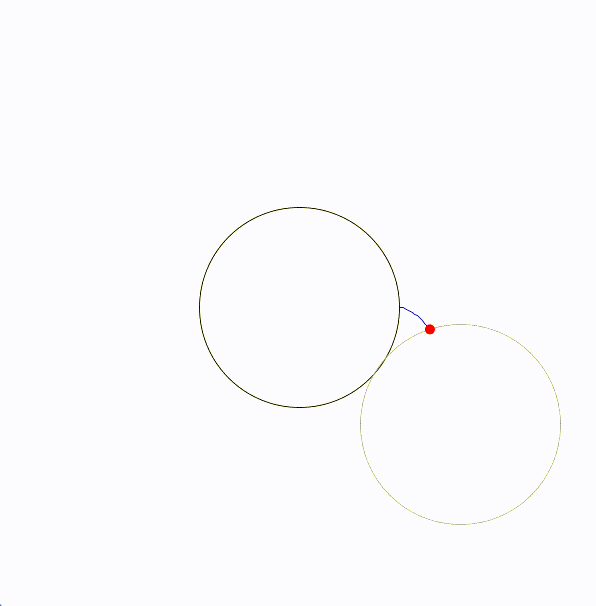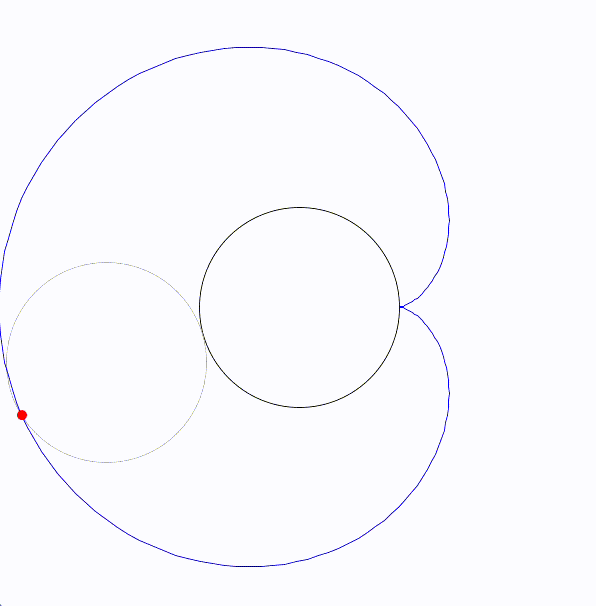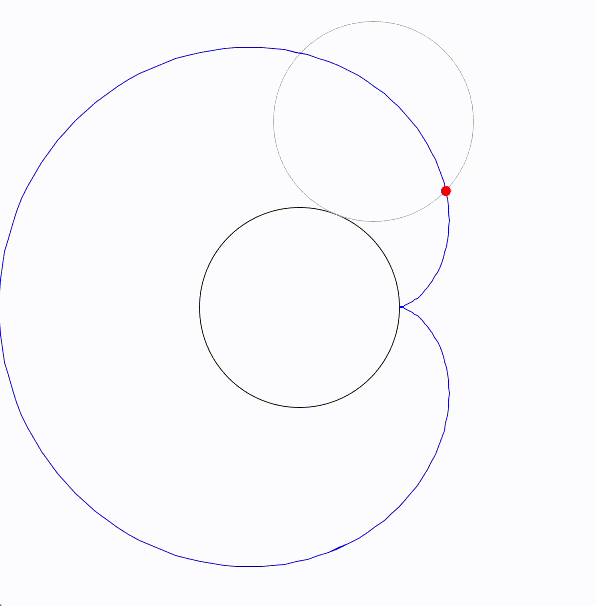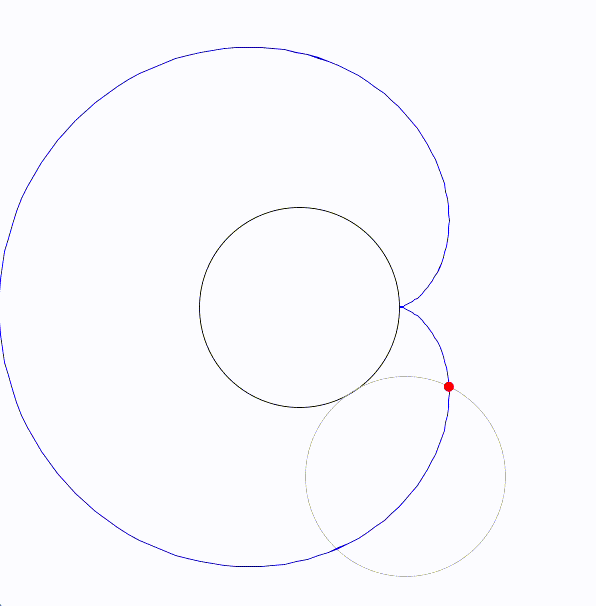
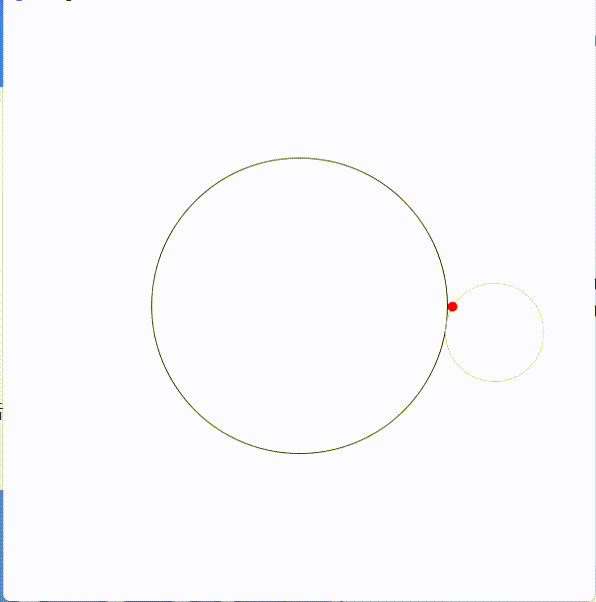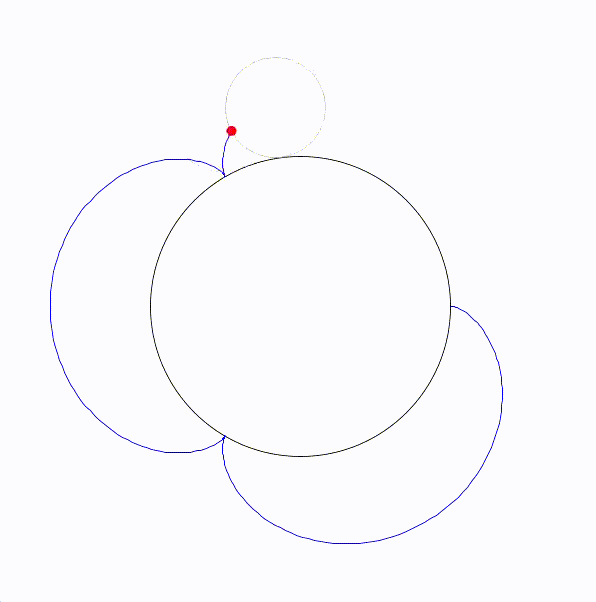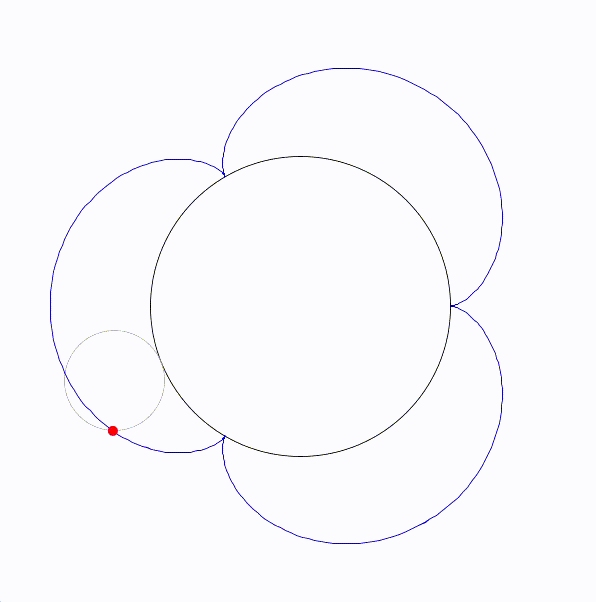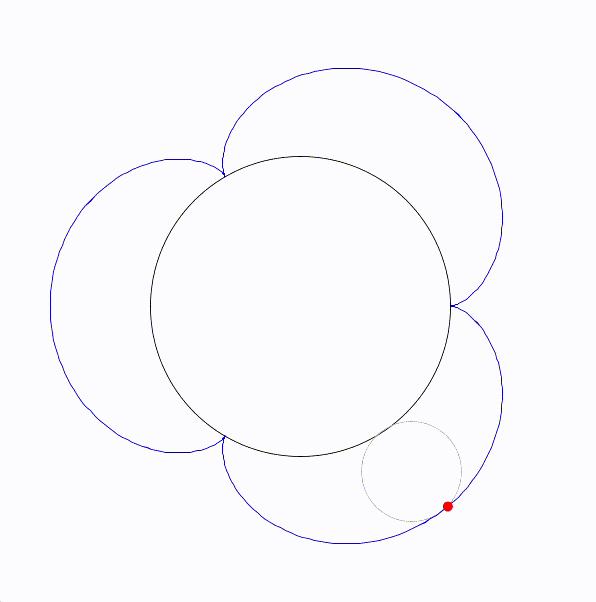
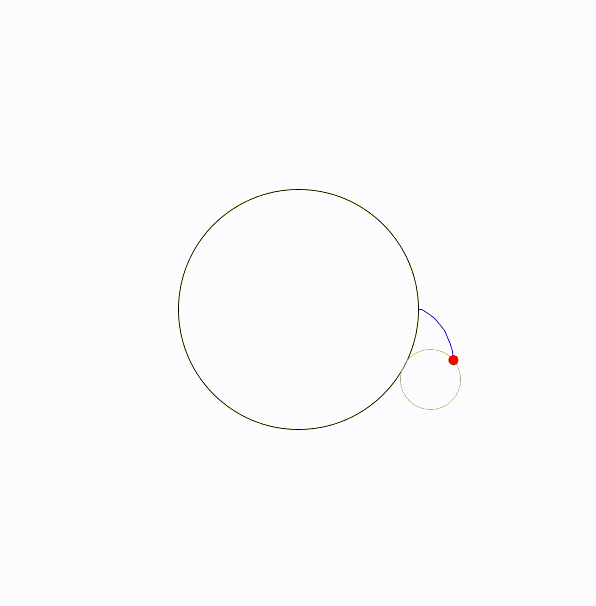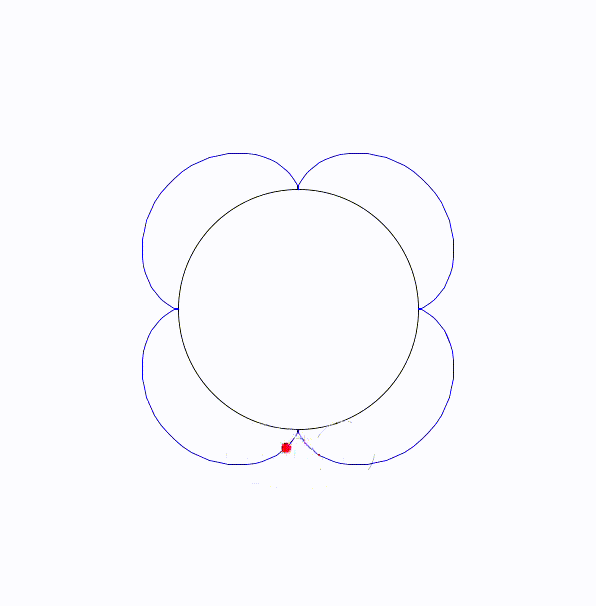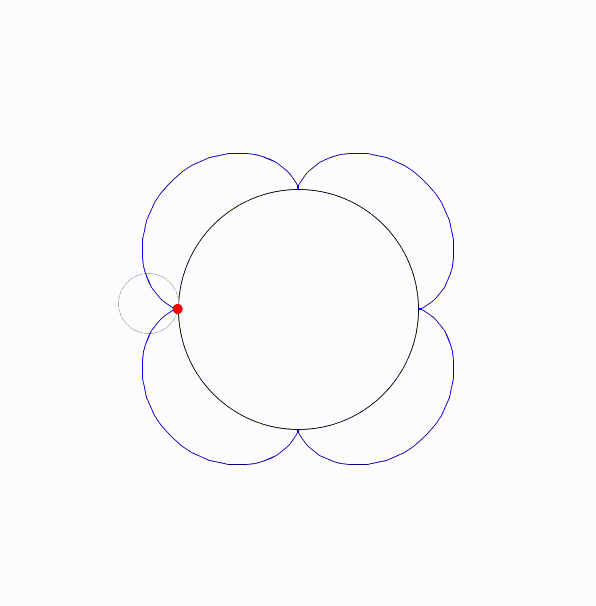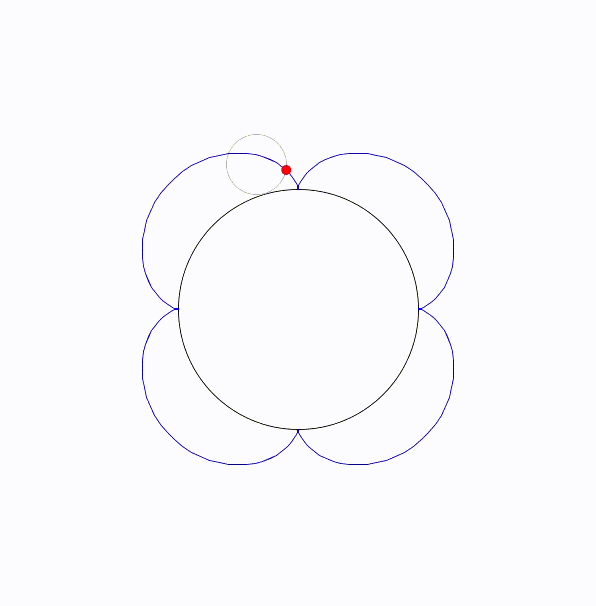
エピサイクロイド曲線（epicycloid）は、円が別の固定された円の外側を転がるときに、転がっている円の一点が描く軌跡です。

1.1. エピサイクロイドの特徴

• 固定円：半径 \( R \) を持つ円が固定されているとします。
• 転がる円：半径 \( r \) を持つ別の円が固定円の外側を滑ることなく転がる状況を考えます。
• 描かれる点：転がる円の外周上の一点（通常は円周上の特定の場所）に注目し、その点が描く軌跡がエピサイクロイド曲線です。

1.2. エピサイクロイドの媒介変数表示

ここで、

• \( x(\theta), y(\theta) \) はエピサイクロイド曲線上の点の座標です。
• \( R \) は固定円の半径です。
• \( r \) は転がる円の半径です。
• $\theta$は0から$2\pi$の範囲です。

2. エピサイクロイドの性質

2.1. エピサイクロイドの導出

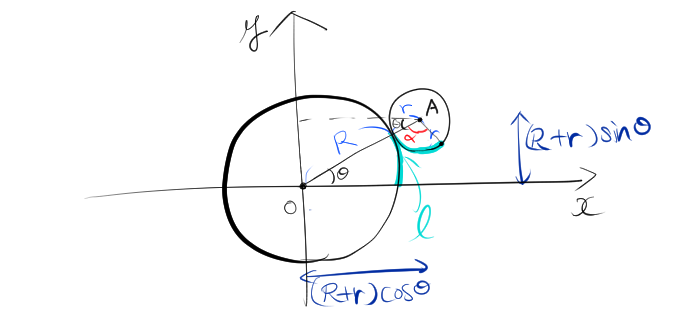
エピサイクロイドを図にすると次のようになります。

図より、$l$の長さが等しいため、

$$R\theta =r\alpha $$

$$\therefore \alpha = \frac{R}{r}\theta$$

点Pの軌跡をベクトルを用いて表す。$\overrightarrow{OP}=\begin{pmatrix} x \\ y \end{pmatrix}$とすると次のようになる。

$$\overrightarrow{OP}=\overrightarrow{OA}+\overrightarrow{AP}$$

$\overrightarrow{OA}$は次のように表すことができる。

$$\overrightarrow{OA}=\begin{pmatrix} (R+r)\cos\theta \\ (R+r)\sin\theta \end{pmatrix}$$

$\overrightarrow{AP}$は次のように表すことができる。

$$\overrightarrow{OA}=\begin{pmatrix} r\cos(\pi+\theta+\alpha) \\ r\sin(\pi+\theta+\alpha) \end{pmatrix}$$

$$=\begin{pmatrix} -r\cos(\theta+\alpha) \\ -r\sin(\theta+\alpha) \end{pmatrix}$$

$$=\begin{pmatrix} -r\cos(\theta+\frac{R}{r}\theta) \\ -r\sin(\theta+\frac{R}{r}\theta) \end{pmatrix}$$

$$=\begin{pmatrix} -r\cos\left(\dfrac{R+r}{r}\theta\right) \\ -r\sin\left(\dfrac{R+r}{r}\theta\right) \end{pmatrix}$$

したがって、

$$\overrightarrow{OP}=\overrightarrow{OA}+\overrightarrow{AP}$$

$$=\begin{pmatrix} (R+r)\cos\theta-r\cos\left(\dfrac{R+r}{r}\theta \right) \\ (R+r)\sin\theta -r\sin\left(\dfrac{R+r}{r}\theta\right) \end{pmatrix}$$

よって、$x$、$y$は次のように表すことができます。

\[ x = (R + r)\cos\theta- r\cos\left(\frac{R + r}{r}\theta\right) \]

\[ y = (R + r)\sin\theta – r\sin\left(\frac{R + r}{r}\theta\right) \]

2.2. $R=kr$と置いたとき

ふゅか

例えば、$R=kr$とすると、$k$の値によって曲線が変わるよね？

はるか

そう。$k=1$だとカージオイド、$k=2$だとネフロイド。

ふゅか

そうそう！$k=3$ならトレフォイロイドで、$k=4$ならクアトロフォイロイド。見た目もそれぞれユニーク！

k=1のとき、カージオイド（cardioid）と呼ばれる。

k=2のとき、ネフロイド（nephroid)と呼ばれる。

k=3のとき、トレフォイロイド（trefoiloid)と呼ばれる。

k=4のとき、クアトロフォイロイド（quatrefoiloid)と呼ばれる。