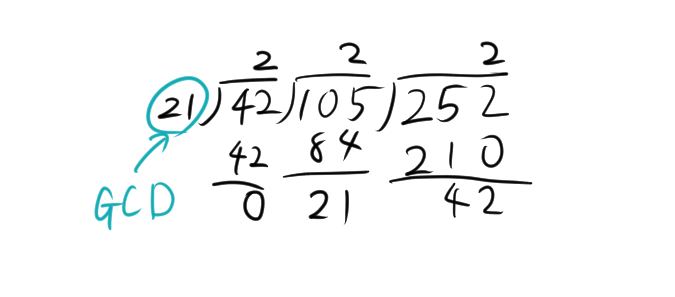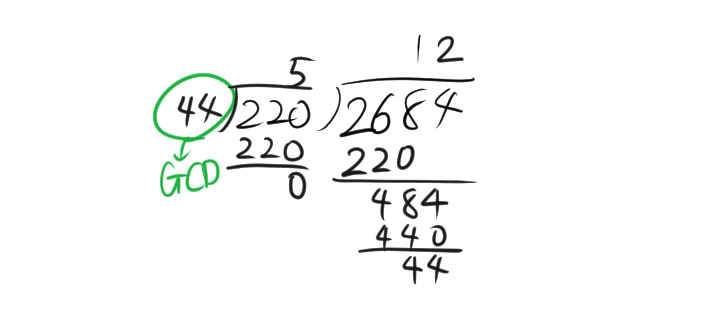ユークリッドの互除法、原理、例題について

はるか

最大公約数を機械的に求めたい。

ふゅか

そういうときは、ユークリッドの互除法が使えるわよ！

1. ユークリッドの互除法

1.1. ユークリッドの互除法の手順

このプロセスを余りが0になるまで繰り返すことで、GCDを求めることができます。

1.2. 例

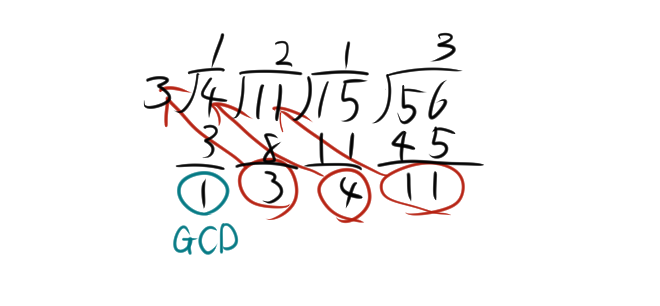
\(a = 56\)、\(b = 15\) の場合

1. \(56\) を \(15\) で割ると、余りは \(56 = 15 \times 3 + 11\)。余り \(r = 11\) 。
2. \(15\) を \(11\) で割ると、余りは \(15 = 11 \times 1 + 4\)。余り \(r = 4\) 。
3. \(11\) を \(4\) で割ると、余りは \(11 = 4 \times 2 + 3\)。余り \(r = 3\) 。
4. \(4\) を \(3\) で割ると、余りは \(4 = 3 \times 1 + 1\)。余り \(r = 1\) 。

したがって、最大公約数は \(1\) です。図にすると、

ふゅか

なんで、互除法は成り立つのかな？

はるか

互除法の原理というものがある。

2. 互除法の原理

2.1. 互除法の原理の証明

$\text{gcd}(a,b)=m,\text{gcd}(b,r)=n$とする。

[1]$a,b$の最大公約数を$m$であるので、$a=ma’$,$b=mb’$として、$a’$と$b’$は互いに素である。

$$r=a-bq =ma’-mb’q = m(a-b’q)$$

つまり、a,bの最大公約数であるmはbとrの公約数でもある。一方で、rとbの最大公約数はnであるから、「$bとrの最大公約数 \geqq bとrの公約数$」が成り立つため、

$$n \geqq m$$

[2]$b,r$の最大公約数を$n$であるので、$b=nb”$,$r=nr”$として、$r”$と$b”$は互いに素である。

$$a=bq+r=nb”q+nr”=n(b”q+r”)$$

つまり、$b,r$の最大公約数であるnはaとbの公約数でもある。一方で、$r$と$b$の最大公約数は$n$であるから、「$aとbの最大公約数 \geqq aとbの公約数$」が成り立つため、

$$m \geqq n$$

[1],[2]より、不等式$n \geqq m$、$m \geqq n$が成り立つので$n=m$である。したがって、「aとbの最大公約数」は、「bとrの最大公約数」となるので、

$$\text{gcd}(a,b)=\text{gcd}(b,r)$$

3. ユークリッドの互除法の例題

3.1. 例題1

1. 252を105で割ります。\( 252 \div 105 = 2 \) 余り \( 42 \)
   → \( 252 = 105 \times 2 + 42 \)
2. 次に、105を42で割ります。\( 105 \div 42 = 2 \) 余り \( 21 \)
   → \( 105 = 42 \times 2 + 21 \)
3. 次に、42を21で割ります。\( 42 \div 21 = 2 \) 余り \( 0 \)
   → \( 42 = 21 \times 2 + 0 \)

したがって、252と105の最大公約数 (GCD) は 21 です。図にすると

3.2. 例題2

1. 2684を220で割ります。\( 2684 \div 220 = 12 \) 余り \( 44 \)
→ \( 2684 = 220 \times 12 + 44 \)

2. 220を44で割ります。次に、\( 220 \div 44 = 5 \) 余り \( 0 \)
→ \( 220 = 44 \times 5 + 0 \)

したがって、2684と220の最大公約数 (GCD) は 44 です。