【互いに素】オイラー関数φの性質と証明、例題について
1. オイラー関数
1.1. オイラー関数の定義
集合を用いて書くと、
\[ \phi(n) = | \text{\{ } m \in \mathbb{N} | 1 \leq m \leq n, \ \gcd(n, m) = 1 \text{ \}} | \]
ここで、\( \gcd(n, m) \) は \( n \) と \( m \) の最大公約数を指し、最大公約数が 1 である場合、 \( n \) と \( m \) は互いに素（coprime）です。
- オイラー関数・・・オイラー関数はオイラーのトーシェント関数とも呼ばれます。
- トーシェント・・・英語で、totient。互いに素である数の個数を意味する。
- 写像・・・$\phi: \mathbb{N}\to\mathbb{N}$となります。
1.2. オイラー関数の計算
$$\varphi(n)=n\left(1 – \frac{1}{p_1}\right) \times \left(1 – \frac{1}{p_2}\right) \times \dots \times \left(1 – \frac{1}{p_k}\right)$$
\( n = 12 \) の場合を考えてみます。
- 素因数分解：\( 12 = 2^2 \times 3 \)
- 公式を利用した計算： \[ \phi(12) = 12 \times \left(1 – \frac{1}{2}\right) \times \left(1 – \frac{1}{3}\right) = 12 \times \frac{1}{2} \times \frac{2}{3} = 4 \] 実際に、1, 5, 7, 11 の4つが12と互いに素です。
1.3. オイラー関数の直感的な意味
nを次のように素因数分解できるとします。
\[ n = p_1^{e_1} p_2^{e_2} \cdots p_k^{e_k} \]
オイラー関数の直感的な意味を考えてみます。
まず、\( n \) には \( p_1, p_2, \ldots, p_k \) という異なる素数が含まれています。これらの素数の倍数にあたる数は、\( n \) と互いに素ではありません。
\( \left( 1 – \frac{1}{p_i} \right) \) という項は、素数 \( p_i \) の倍数に該当する数の割合を取り除く操作を意味します。
たとえば、ある素数 \( p_1 \) が \( n \) に含まれているとします。このとき、1 以上 \( n \) 以下の数の中で、\( p_1 \) と互いに素である数の個数は次のように求めることができます。
$$n – \frac{n}{p_1} = n \left( 1 – \frac{1}{p_1} \right)$$
この式は、\( n \) から \( p_1 \) の倍数を取り除いた数、つまり \( p_1 \) と互いに素である数の個数を表しています。
次に、別の素数 \( p_2 \) も \( n \) に含まれている場合を考えます。この場合、先ほどの \( p_1 \) によって除外された数に対して、さらに \( p_2 \) の倍数を除去します。これを式で表すと、次のようになります。
$$n \left( 1 – \frac{1}{p_1} \right) \left( 1 – \frac{1}{p_2} \right)$$
つまり、\( n \) から \( p_1 \) と \( p_2 \) の倍数を除外した結果、これらの素数と互いに素である数の個数が求められます。この操作を他の素数についても繰り返すことで、指定されたすべての素数と互いに素である数の個数を求めることができます。
2. オイラー関数の性質
2.1. 素数のオイラー関数
$$\varphi(p)=p-1$$
\( p \) が素数である場合、1 から \( p \) までの数のうち、\( p \) 自身を除くすべての数は \( p \) と互いに素です。
よって、\( p \) と互いに素である数の個数は \( p-1 \) です。
したがって、オイラー関数の定義に従って、素数 \( p \) に対して
\[ \varphi(p) = p – 1 \]
が成り立ちます。
2.2. $p^k$のオイラー関数
\( p \) を素数、\( k \) を正の整数とします。\( \varphi(p^k) \) を求める際、\( p^k \) 以下の自然数のうち、\( p^k \) と互いに素であるものの個数を考えます。
\( p^k \) と互いに素でない数は、\( p \) の倍数である数です。これらの数は \( p, 2p, 3p, \ldots, p^{k-1}p \) であり、その個数は \( p^{k-1} \) 個あります。
\( p^k \) 以下のすべての自然数の個数は \( p^k \) です。
よって、\( p^k \) 以下のすべての数のうち、\( p \) の倍数ではない数、つまり \( p^k \) と互いに素である数の個数は「\( p^k \) 以下のすべての自然数の個数$-$\( p \) の倍数である数の個数」であるので、
\[ \varphi(p^k) = p^k – p^{k-1} \]
この式は、次のように因数分解することができます。
\[ \varphi(p^k) = p^{k-1}(p – 1) \]
さらに、この式を次のように書き換えることができます。
\[ \varphi(p^k) = p^k \left(1 – \frac{1}{p}\right) \]
2.3. 乗法的性質
$0からmn-1$の$mn$個の数をm個ずつ並べると、次のようになります。
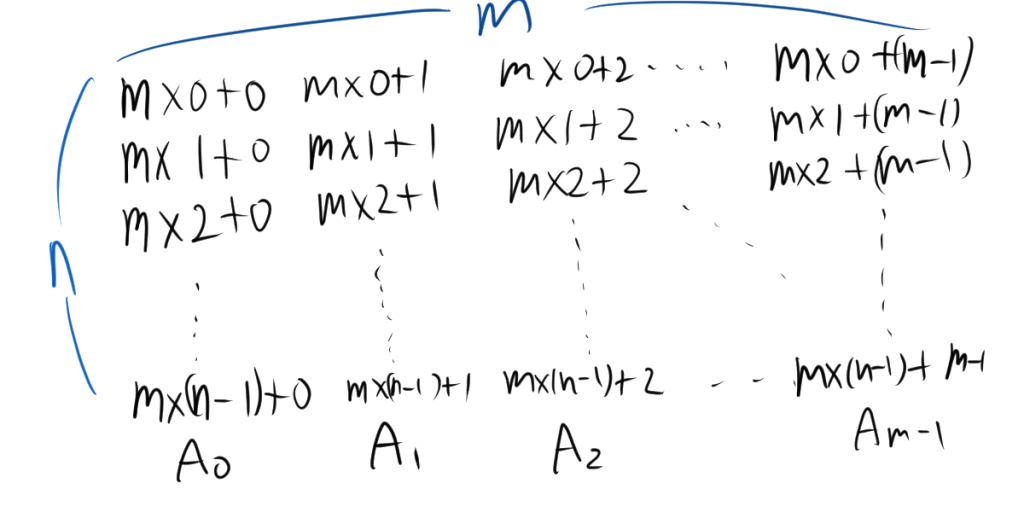ここで、図の縦の集合、つまり、mで割った同じあまりの集合$A_r$を
$$A_r = \{ m\times 0+r,m\times 1 + r ,m\times 2 + r \cdots, m\times(n-1) +r\}$$
とする。
$r$ と $m$ が互いに素でないとき、つまり $\gcd(r, m) \neq 1$ の場合、集合 $A_r$ の各要素 $m \times k + r$ (ここで $k$ は $0 \leq k \leq n-1$) も $m$ と共通の約数を持つ。mと共通の約数を持つため、rとmnも共通の約数を持つ。したがって、これらの数はすべて $mn$ と互いに素ではありません。
$r$ と $m$ が互いに素であるとき、つまり $\gcd(r, m) = 1$ の場合を考えます。このとき、集合 $A_r$ の各要素 $m \times k + r$ は、$m$ と互いに素であるため、これらの数は $mn$ と互いに素である可能性があります。
ここで、$A_r$ の要素は$m$ と互いに素であることを考慮すると、 nと互いに素である数を考えればいいので、mnと互いに素である数の個数は $\varphi(n)$ になります。このような、mと互いに素な集合$A_r$は$\varphi(m)$個存在するので、
$$\varphi(mn) =\varphi(m)\varphi(n)$$
2.4. 互いに素な数の個数
ここで、\( p \) は \( n \) の異なる素因数です。$\prod$は総乗の記号です。
nは次のように素因数分解することができるとすると、
$$n=p_1^{e_1}p_2^{e_2}\cdots p_k^{e_k}$$
オイラー関数の乗法的性質を利用すると
$$\varphi(n)=\varphi(p_1^{e_1})\varphi(p_2^{e_2})\cdots\varphi(p_k^{e_k})$$
$\varphi(p^k) = p^k \left(1 – \frac{1}{p}\right)$より、
$$\varphi(n)=p_1^{e_1}p_2^{e_2}\cdots p_k^{e_k}\left(1 – \frac{1}{p_1}\right) \times \left(1 – \frac{1}{p_2}\right) \times \dots \times \left(1 – \frac{1}{p_k}\right)$$
したがって、$n=p_1^{e_1}p_2^{e_2}\cdots p_k^{e_k}$より、
$$\varphi(n)=n\left(1 – \frac{1}{p_1}\right) \times \left(1 – \frac{1}{p_2}\right) \times \dots \times \left(1 – \frac{1}{p_k}\right)$$
3. 例題
- \( n = 48 \)
- \( n = 108 \)
- \( n = 360 \)
1. \( n = 48 \)の場合
- \( 48 \) の素因数分解は \( 48 = 2^4 \times 3 \)。
- オイラー関数の公式に従い、\( \phi(48) \) を求める： \[ \phi(48) = 48 \times \left(1 – \frac{1}{2}\right) \times \left(1 – \frac{1}{3}\right) = 48 \times \frac{1}{2} \times \frac{2}{3} = 16 \]
2. \( n = 108 \)の場合
- \( 108 \) の素因数分解は \( 108 = 2^2 \times 3^3 \)。
- オイラー関数の公式に従い、\( \phi(108) \) を求める： \[ \phi(108) = 108 \times \left(1 – \frac{1}{2}\right) \times \left(1 – \frac{1}{3}\right) = 108 \times \frac{1}{2} \times \frac{2}{3} = 36 \]
3. \( n = 360 \)の場合
- \( 360 \) の素因数分解は \( 360 = 2^3 \times 3^2 \times 5 \)。
- オイラー関数の公式に従い、\( \phi(360) \) を求める： \[ \phi(360) = 360 \times \left(1 – \frac{1}{2}\right) \times \left(1 – \frac{1}{3}\right) \times \left(1 – \frac{1}{5}\right) = 360 \times \frac{1}{2} \times \frac{2}{3} \times \frac{4}{5} = 96 \]
以上より、答えをまとめると
- \( \phi(48) = 16 \)
- \( \phi(108) = 36 \)
- \( \phi(360) = 96 \)
