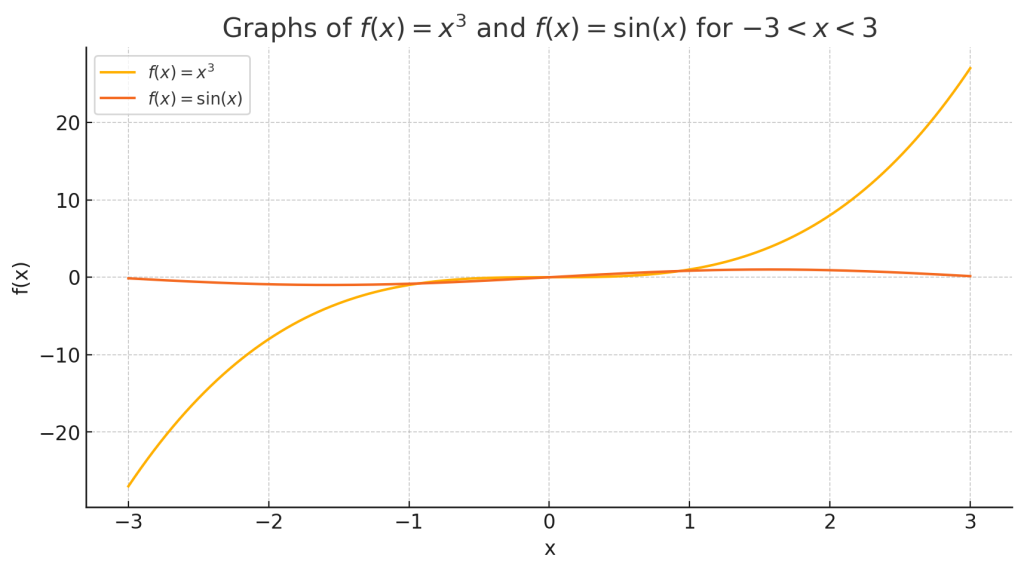偶関数と奇関数の定義・積分の性質・具体例についてわかりやすく解説

1. 偶関数
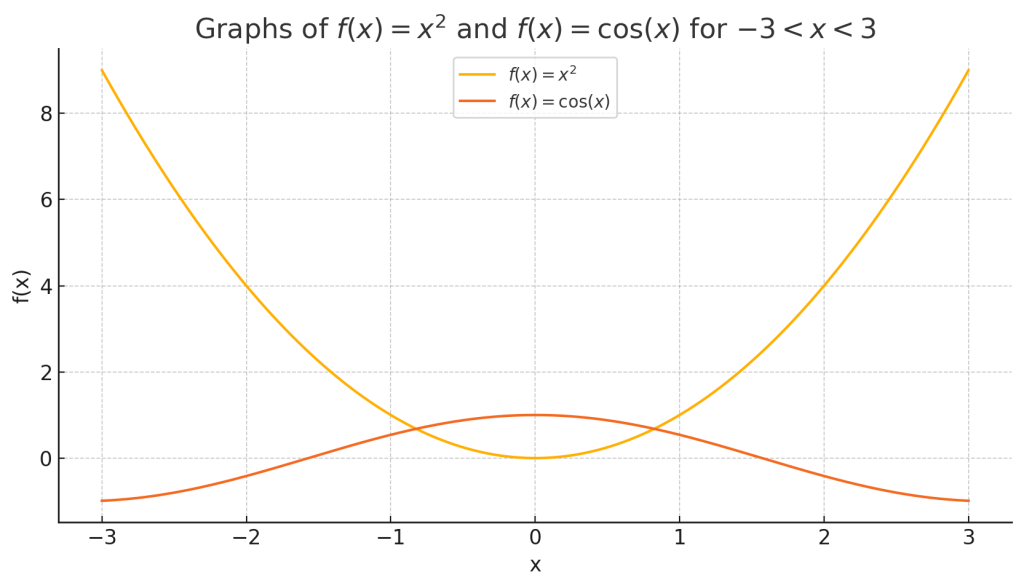
これは、関数のグラフが y 軸に対して対称であることを意味します。つまり、x の正負を反転させても関数の値は変わりません。
1.1. 偶関数の例
- \( f(x) = x^2 \)
- \( f(x) = \cos(x) \)
2. 奇関数
これは、関数のグラフが原点に対して対称であることを意味します。つまり、x の正負を反転させると関数の値も反転します。
2.1. 奇関数の例
- \( f(x) = x^3 \)
- \( f(x) = \sin(x) \)
3. 偶関数と奇関数の積分の性質
3.1. 偶関数の積分
\[ \int_{-a}^{a} f(x) \, dx = 2 \int_{0}^{a} f(x) \, dx \]
偶関数 \( f(x) \) とは、すべての \( x \) について \( f(-x) = f(x) \) を満たす関数のことです。
関数 \( f(x) \) を区間 \([-a, a]\) で積分します。
\[ \int_{-a}^{a} f(x) \, dx = \int_{-a}^{0} f(x) \, dx + \int_{0}^{a} f(x) \, dx \]
置換 \( u = -x \) を使って、積分を変換します。
\[ \int_{-a}^{0} f(x) \, dx = \int_{a}^{0} f(-u) \, (-du) = \int_{0}^{a} f(-u) \, du = \int_{0}^{a} f(u) \, du \]
これにより、全体の積分は
\[ \int_{-a}^{a} f(x) \, dx = \int_{0}^{a} f(x) \, dx + \int_{0}^{a} f(x) \, dx = 2 \int_{0}^{a} f(x) \, dx \]
3.2. 奇関数の積分
\[ \int_{-a}^{a} g(x) \, dx = 0 \]
奇関数 \( g(x) \) とは、すべての \( x \) について \( g(-x) = -g(x) \) を満たす関数のことです。
関数 \( g(x) \) を区間 \([-a, a]\) で積分します。
\[ \int_{-a}^{a} g(x) \, dx = \int_{-a}^{0} g(x) \, dx + \int_{0}^{a} g(x) \, dx \]
置換 \( u = -x \) を使って、積分を変換します。
\[ \int_{-a}^{0} g(x) \, dx = \int_{a}^{0} g(-u) \, (-du) = -\int_{0}^{a} g(-u) \, du = -\int_{0}^{a} g(u) \, du \]
これにより、全体の積分は
\[ \int_{-a}^{a} g(x) \, dx = \int_{0}^{a} g(x) \, dx + \left( -\int_{0}^{a} g(x) \, dx \right) = 0 \]
4. 偶関数・奇関数の具体例
4.1. 偶関数の例
$f(x) = x^2$であるとする。
\[ f(-x) = (-x)^2 = x^2 \]
よって、\( f(x) = f(-x) \) となり、これは偶関数です。
4.2. 奇関数の例
$ f(x) = x^3 $であるとする。
\[ f(-x) = (-x)^3 = -x^3 \]
よって、\( f(-x) = -f(x) \) となり、これは奇関数です。