私たちの身の回りには、「次に何かが起こるまでの時間」を扱う場面がたくさんあります。たとえば、バスが来るまでの時間、ある機械が故障するまでの時間、あるいは電話が鳴るまでの時間などです。
こうした「待ち時間」をモデル化する際に登場するのが指数分布という確率分布です。
この記事では、指数分布の確率密度関数から始めて、期待値や分散の計算方法、さらに指数分布特有の「無記憶性」という性質について、やさしく丁寧に解説していきます。数式にも触れますが、ひとつひとつの意味を理解しながら読み進めていただければ、指数分布がぐっと身近に感じられるはずです。
それでは、まずは指数分布の基本となる確率密度関数から見ていきましょう。

はるか

ふゅか
簡単に言うと、「次に何かが起こるまでの時間」を表すときによく使われる分布だよ。

はるか
1. 確率密度関数
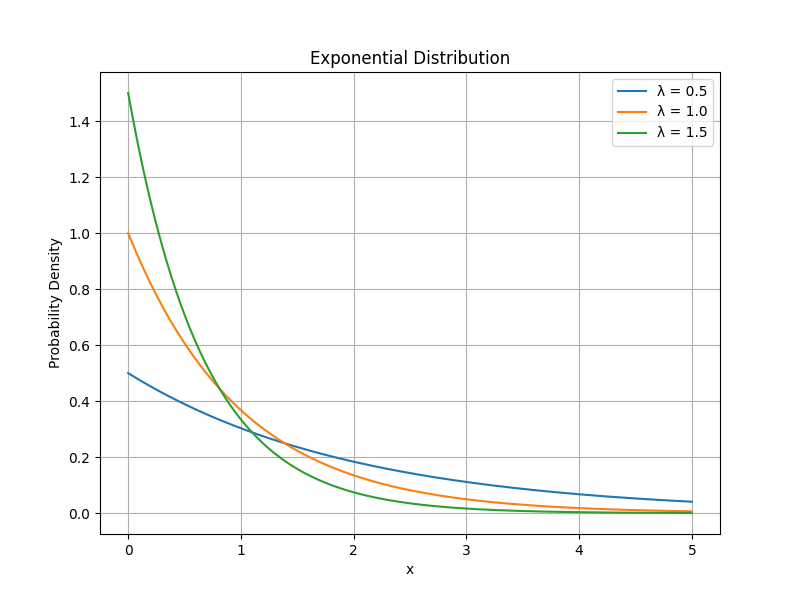
指数分布の確率密度関数は次の式で表されます。
f(x)={λe−λx0(x≥0)(x<0)
2. 期待値と分散
指数分布の期待値E[X]と分散V[X]は 次のようになります。
E[X]=λ1 V[X]=λ21
指数分布の期待値と分散の計算は、積分を使用して行います。
2.1. 期待値 E[X] の計算
期待値は次のようになります。
E(X)=∫0∞xf(x) dx=∫0∞xλe−λxdx
ここで部分積分を使います。
∫0∞xλe−λxdx=[−xe−λx]0∞+∫e−λxdx
無限大での xe−λx の値は 0 に収束し、下限は 0 です。そのため、残る積分は、
∫0∞e−λx dx=[λ−1e−λx]0∞=λ1
したがって、
E(X)=λ1
2.2. 分散 V[X] の計算
分散は Var(X)=E(X2)–[E(X)]2 で定義されます。まず E(X2) を計算します:
E(X2)=∫0∞x2λe−λxdx
部分積分を適用すると、
∫x2λe−λxdx=[−x2e−λx]0∞+∫0∞2xe−λxdx
前述の E(X) の計算で求めた ∫xe−λxdx=λ21 を利用すると、
∫0∞2xe−λxdx=2×λ21=λ22
したがって、
E(X2)=λ22
よって、分散は
V[X]=λ22–(λ1)2=λ21
指数分布の期待値と分散が E[X]=λ1、V[X]=λ21 であることがわかりました。
3. 指数分布の無記憶性
指数分布の特性の一つに「無記憶性」があります。数学的には次のように表されます。
P(X>s+t∣X>s)=P(X>t)

ふゅか
ある時点での事象が次の時間の事象には依存しないという性質です。
3.1. 無記憶性の証明
指数分布が無記憶性を持つことを示すには、以下の等式を証明します。
P(X>s+t∣X>s)=P(X>t)
3.1.1. ステップ 1: 左辺の計算
条件付き確率の定義により、左辺は次のように計算できます。
P(X>s+t∣X>s)=P(X>s)P((X>s+t)∩(X>s))
(X>s+t)∩(X>s))はX>s+t より、
P(X>s+t∣X>s)=P(X>s)P(X>s+t)
3.1.2. ステップ 2: P(X>x) の計算
指数分布において、P(X>x)は次のように計算されます。
P(X>x)=∫x∞λe−λydy=e−λx
これを使って、分母と分子を計算する。
P(X>s+t)=e−λ(s+t)P(X>s)=e−λs
3.1.3. ステップ 3: 条件付き確率の計算
これらを条件付き確率の式に代入します。
P(X>s+t∣X>s)=e−λse−λ(s+t)=e−λt=P(X>t)
これにより、指数分布が無記憶性の性質を持つことが示されました。






