指数関数とは?指数関数のグラフと性質、応用について

ふゅか
指数関数って色々なところで使われているのよ!例えば、複利計算とか人口増加とか♪
はるか
うん。数学でもよく出てくる。
1. 指数関数とは
1.1. 指数関数
指数関数とは、次のような形をした関数のことです。
\[ f(x) = a^x \]
ここで、\(a\) は正の定数(通常は \(a > 0\) で \(a \neq 1\))、\(x\) は変数です。この式は、 \(a\) の \(x\) 乗を表します。たとえば、\(a = 2\) の場合、指数関数は次のようになります。
\[ f(x) = 2^x \]
1.2. ネイピア数
最もよく使われる指数関数の底は、自然対数の底(ネイピア数)\(e\) です。\(e\) は約 2.718 で、次のような形になります。
\[ f(x) = e^x \]
この関数は、微分しても変わらない関数として知らている。
2. 指数関数のグラフ
指数関数のグラフは、基数によって異なります。例えば、\(a > 1\) の場合、グラフは急激に上昇し、\(0 < a < 1\) の場合、緩やかに下降します。次のグラフは、底が 2 と 1/2 の場合の例です。
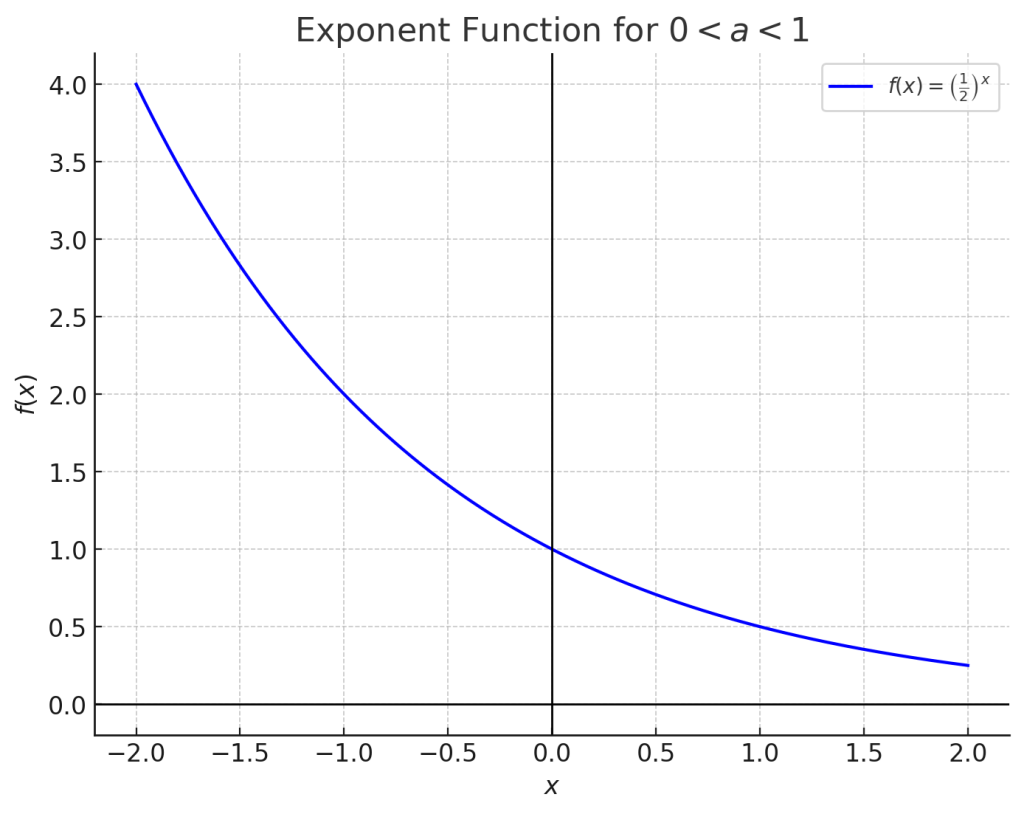
2.1. \( 0 < a < 1 \) の場合
この範囲では、底 \( a \) の値が1より小さい正の数になります。
- 単調減少:\( x \) が増加すると、関数 \( a^x \) は減少します。つまり、$x_1<x_2$に対して、$f(x_1)>f(x_2)$になります。
- 正の値を取る:どの \( x \) に対しても \( a^x \) は常に正の値を取り、負の値にはなりません。
- グラフの特徴:グラフは \( x \to \infty \) で \( 0 \) に近づきます。一方で、\( x \to -\infty \) のときは \( 0 \) に急激に上昇ます。
例えば、\( a = \dfrac{1}{2} \) を考えてみましょう。\( f(x) = \left(\dfrac{1}{2}\right)^x \)とすると、
- \( f(0) = 1 \)
- \( f(1) = \frac{1}{2} \)
- \( f(2) = \frac{1}{4} \)
$0<1<2$となり、$f(0)>f(1)>f(2)$となり単調減少になっています。また、グラフは右肩下がりの曲線になります。
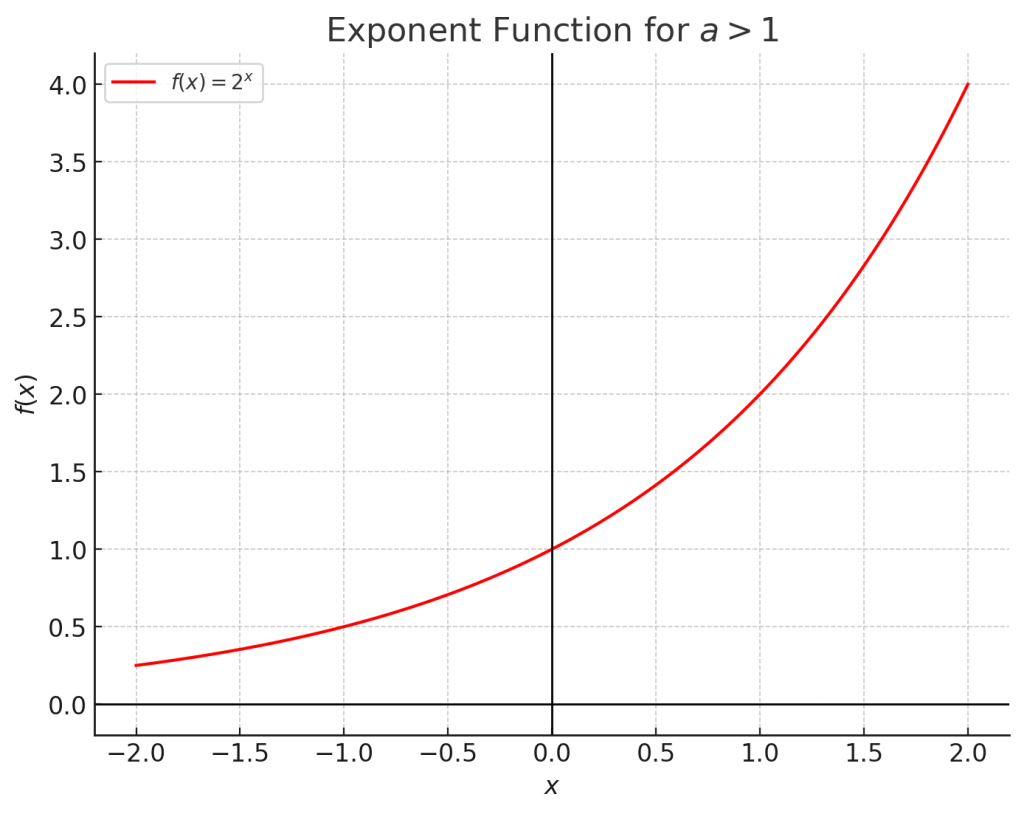
2.2. \( a > 1 \) の場合
$a > 1$の範囲では、底 \( a \) の値が1より大きくなります。
- 単調増加:\( x \) が増加すると、関数 \( a^x \) は急激に増加します。つまり、$x_1<x_2$に対して、$f(x_1)<f(x_2)$になります。
- 正の値を取る:どの \( x \) に対しても、\( a^x \) は常に正の値です。
- グラフの特徴:グラフは \( x \to \infty \) で急激に上昇しますが、\( x \to -\infty \) のときは \( 0 \) に近づきます。
例えば、\( a = 2 \) をを考えてみましょう。\( f(x) = 2^x \)とすると、
- \( f(0) = 1 \)
- \( f(1) = 2 \)
- \( f(2) = 4 \)
$0<1<2$となり、$f(0)<f(1)<f(2)$となり単調増加になっています。また、グラフは右肩上がりの急な曲線になります。
はるか
急激に増加する。グラフを見るとわかる。
ふゅか
うん、まるでジェットコースターみたいに急に上がる感じ!この変化の速さがすごいのよ♪
3. 指数関数の応用
指数関数は、日常生活や科学技術においても非常に重要です。例えば、以下のような場面で活用されます。
- 複利計算:銀行預金や投資の利息計算で、指数関数は重要な役割を果たします。複利計算は、時間が経つごとに利息が利息に対しても計算されるため、指数関数的に増加します。
- 人口増加:人口の増加や細胞分裂などの現象は、指数関数で表現されることが多いです。一定の割合で増加する現象をモデル化する際に便利です。
- 放射性物質の崩壊:放射性物質の崩壊速度も指数関数で表され、一定時間ごとに物質が半減する「半減期」が指数関数的な性質を持っています。
PR