【底に注意!!】指数不等式の解き方と例題について

1. 指数不等式とは?
例えば、次のような形をした不等式がそれに該当します。
\[ 2^x > 16 \]
\[ 3^x \leq 27 \]
2. 基本的な解き方
2.1. 底を揃える
指数関数の底(基数)が同じ場合、指数の部分を直接比較することができます。例えば、
\[ 2^x > 16 \]
この式では、右辺の16を2のべき乗に書き換えます。
\[ 2^x > 2^4 \]
このとき、底が同じ「2」なので、指数の部分を比較して次のような不等式に変形できます。
\[ x > 4 \]
2.2. 底に注意!!
底が分数である場合、特に底が \(0 < a < 1\) の範囲にあるとき、不等式の向きに注意が必要です。次のように、底が分数である場合の不等式を考えます。
$$\left(\frac{1}{101}\right)^x > \left(\frac{1}{101}\right)^{101} $$
直感的に$x>101$としたいところですが、ちょっと待て!!!!!!!!
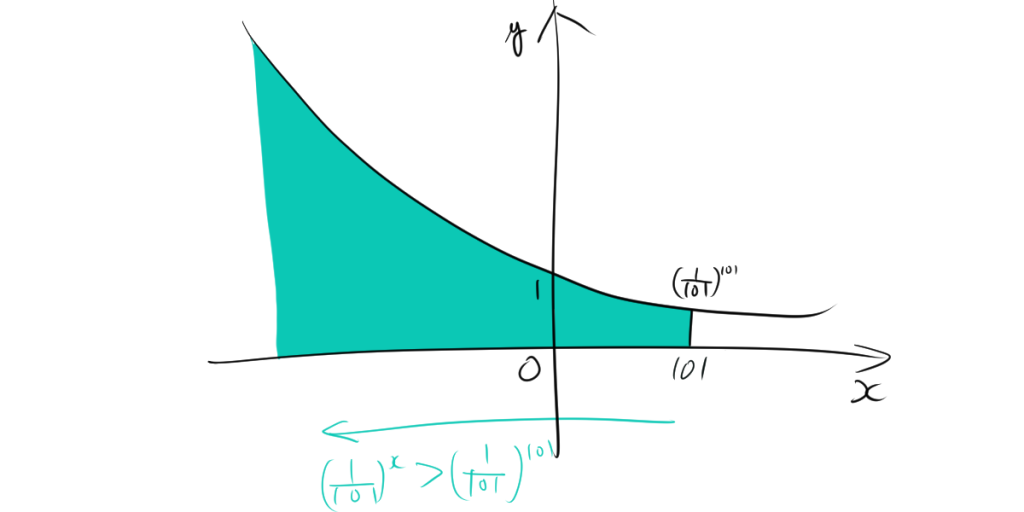
いったん、指数関数のグラフを考えてみよう。
$\left(\frac{1}{101}\right)^x > \left(\frac{1}{101}\right)^{101} $となる範囲は、$x<101$となっています。
このように、底が0<a<1の場合は指数不等式を比較する際、不等式の向きが反転します。
$$a^x > a^y \Leftrightarrow x>y$$
$0<a<1$のとき、 不等式の向きは反転して
$$a^x > a^y \Leftrightarrow x<y$$
これが、指数方程式の問題とは違う部分です。また、対数をとるときも、同様に考えれば問題ないです。
2.3. 対数を使う場合
底が異なる場合、直接指数部分を比較することが難しいです。このような場合、対数を使って解きます。例えば次の不等式を考えてみます。
\[ 5^x \leq 20 \]
このままでは解きにくいので、5を底として対数を取ります。
\[ \log_5(5^x) \leq \log_5(20) \]
対数の性質を使うと、
\[ x \leq1+2\log 5\]
3. 指数不等式の例題
3.1. 例題1
\[ 3^{2x-1} > 81 \]
まず、右辺の81を3のべき乗に直します。
\[ 3^{2x-1} > 3^4 \]
底が揃ったので、指数部分を比較します。
\[ 2x – 1 > 4 \]
これを解いて、
\[ 2x > 5 \]
\[ x > \frac{5}{2} \]
したがって、解は \( x > \frac{5}{2} \) となります。
3.2. 例題2
\[ \left(\frac{1}{2}\right)^{2x}-\left(\frac{1}{2}\right)^x > 42\]
まず、置き換えを行います。
\[ t = \left( \dfrac{1}{2} \right)^x \]
\(\dfrac{1}{2}\)は正の数であり、正の数の任意の実数乗は正なので、\(t > 0\) です。
この置き換えを不等式に代入すると。
\[ t^2 – t – 42 > 0 \]
\[ (t – 7)(t + 6) > 0 \]
したがって、\(t > 7\) のときに不等式が成り立ちます。
\[ \left( \dfrac{1}{2} \right)^x > 7 \]
$\frac{1}{2}$で対数をとって、
\[ \log_{\frac{1}{2}}\left( \left( \dfrac{1}{2} \right)^x \right) < \log_{\frac{1}{2}} 7 \]
したがって、
\[ x < \log_{\frac{1}{2}} 7 \]