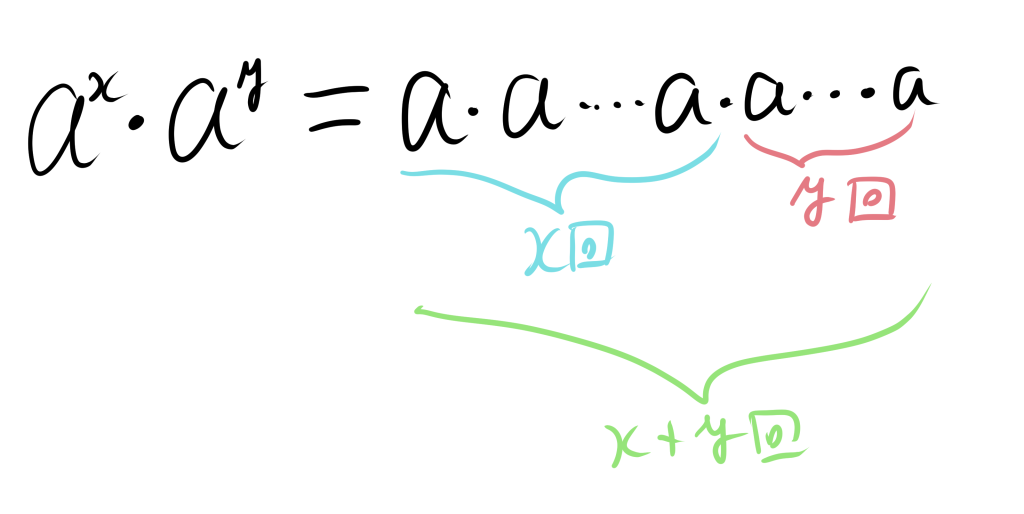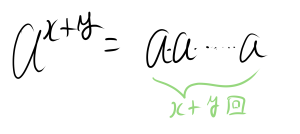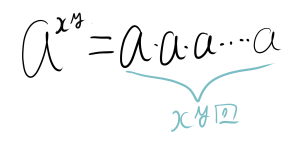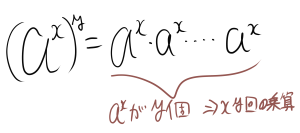【a^0=1】指数法則の意味と具体例、例題について

1. 指数法則
1.1. $a^{x+y}=a^x\cdot a^{y}$
この数式は、同じ底を持つ指数の和は、それぞれの指数を個別に計算した結果を乗じたものと等しいことを表しています。まず、$a^x$と$a^y$を考えます。これらは、それぞれ$a$を$x$回、$y$回かけたものです。したがって、
となります。一方、$a^{x+y}$は、$a$を$x+y$回かけたものです。したがって、
となります。
ここで、$a^x\cdot a^y$と$a^{x+y}$を比較してみると、前者は$a$を$x$回かけたものに、$a$を$y$回かけたものをかけたものであり、後者は$a$を$x+y$回かけたものであることがわかります。つまり、両者は同じ回数だけaを乗算していると考えられます。
したがって、$a^{x+y}=a^x\cdot a^{y}$となります。
$3^5$を例にして考えてみましょう。
$3^{2+3}$
$=3^5$
$=3\times3\times3\times3\times3$
$=(3\times3)\times(3\times3\times3)$
$=3^2\times 3^3$
1.2. $a^{xy}=(a^{x})^{y}=(a^{y})^{x}$
まず、$a^{xy}$を考えます。これは、$a$を$xy$回かけたものです。つまり、
となります。
次に、$(a^{x})^{y}$を考えます。これは、$a$を$x$回かけたものを、$y$回かけたものをかけたものです。したがって、
となります。よって、この式は$a^{xy}$と等しくなります。
また、$(a^{y})^{x}$を考えると、これは$y$回かけたものを、$x$回かけたものをかけたものですが、先ほどと同様に指数の乗法法則を用いて、$a^{xy}$と等しくなります。
$2^6$を例にして考えてみましょう。
$(2^3)^2=8^2=64$
$(2^2)^3=4^3=64$
$2^6=64$
となっているため、
$2^6=(2^2)^3=(2^3)^2$
となります。
1.3. $a^{\frac{1}{x}}=\sqrt[x]{a}$
この数式は、底が$a$で指数が$\frac{1}{x}$である数値を、$x$乗根として表すことができるという意味を持ちます。
具体例を挙げると、$2^{\frac{1}{3}}$は、$2$の$3$乗根を表します。これは、$2$を$3$乗したら$2$になります。同様に、$4^{\frac{1}{2}}$は、$2$となります。
1.4. $a^{-x}=\displaystyle\frac{1}{a^x}$
$a^{-x}$は$a$を底とする指数関数の逆数です。
例えば、$a=2、x=3$の場合、$a^{-x}$は$1/2^3$、すなわち$1/8$となります。
2. $a^0=1$を証明する
まず、$a^0 = a^{n – n}$となります。ここで、nは任意の自然数です。
次に、指数の差の公式を用いて、
$a^{n – n}$
$=a^n\cdot a^{-n}$
$= \dfrac{a^n}{ a^n}$
と変形できます。
ここで、$\dfrac{a^n} { a^n }= \dfrac{a × a × … × a} {a × a × … × a}$であることに着目します。この分数の分子と分母は、同じ数aをn個かけたものであり、各項がそれぞれ等しいため、分子と分母が約分されて1になります。
したがって、$a^0 = 1$となります。
3. 指数法則の例題
3.1. 例題1
$(2^3 × 3^2)^2 ÷ (2^2 × 3^3)$
$$\begin{align*}&(2^3 × 3^2)^2 ÷ (2^2 × 3^3) \\ &=\dfrac{2^6 × 3^4}{2^2 × 3^3} \\ &=2^4 × 3 \\ &=48 \end{align*} $$
3.2. 例題2
$$(2^{\frac{1}{3}}2^{\frac{1}{5}})^3$$
$$\begin{align*}&(2^{\frac{1}{3}}2^{\frac{1}{5}})^3 \\ &=2^{\left(\frac{1}{5}+\frac{1}{3}\right)3} \\ &=2^{\frac{8}{15}\cdot3} \\ &=48 \end{align*} $$