最大値・最小値の定理の証明、イメージと具体例について

1. 最大値・最小値の定理とは
- \( f(x) \) の最大値 \( M \) が存在して、ある \( c \in [a, b] \) について \( f(c) = M \) を満たす。
- \( f(x) \) の最小値 \( m \) が存在して、ある \( d \in [a, b] \) について \( f(d) = m \) を満たす。
ここで、最大値 \( M \) は \[ M = \max_{x \in [a, b]} f(x) \]
最小値 \( m \) は \[ m = \min_{x \in [a, b]} f(x) \]
1.1. 直感的なイメージ
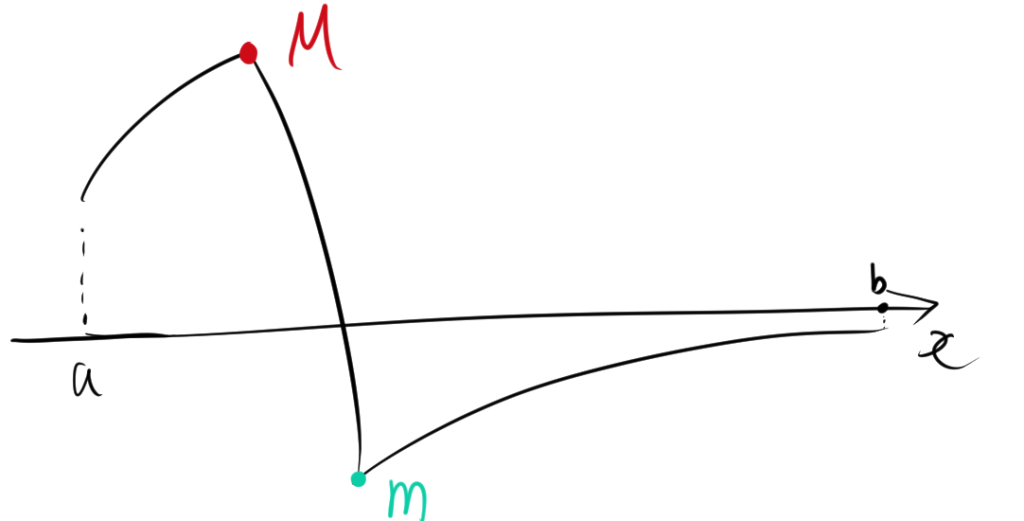
最大値・最小値の定理の直感的なイメージは、山と谷のように連続したグラフが閉区間内にある場合、そのグラフの中で必ず一番高いところ(最大値)と一番低いところ(最小値)がある、というものです。
1.2. 具体例
\( f(x) = x^2 \) を区間 \([-2, 1]\) で考えます。この関数は連続で、閉区間で定義されています。
- 最大値:\( x = -2 \) のとき \( f(-2) = 4 \)
- 最小値:\( x = 0 \) のとき \( f(0) = 0 \)
2. 証明
$f$が最大値を持つことを示せれば、$-f$の最大値、つまり関数$f$が最小値をもつことを示せるので、最大値を持つことのみを示す。
連続関数 \( f \) が閉区間 \( I = [a, b] \) 上で定義されているとする。
\[ M = \sup_{x \in I} f(x) \]
\( f \) は連続関数であり、閉区間上では有界なので、\( M \) は有限の値を取ります。
上限の性質より、任意の自然数 \( n \) に対して、ある点 \( a_n \in I \) が存在して、
\[ M – \frac{1}{n} < f(a_n) \leq M \]
となります。点列 \( \{a_n\} \subset I \) が得られ、はさみうちの原理より、\( f(a_n) \to M \)(\( n \to \infty \))となります。
一方で、閉区間 \( I \) は有界なので、ボルツァノ・ワイエルシュトラスの定理により、\( \{a_n\} \) は収束部分列 \( \{a_{n_k}\} \) を持ちます。つまり、ある \( a \in I \) が存在して、
\[ \lim_{k \to \infty} a_{n_k} = a \]
となります。
関数 \( f \) の連続性より、
\[ \lim_{k \to \infty} f(a_{n_k}) = f\left( \lim_{k \to \infty} a_{n_k} \right) = f(a) \]
となります。
これまでの結果から、
\[ f(a) = \lim_{k \to \infty} f(a_{n_k}) = M \]
となり、\( f \) は点 \( a \in I \) で最大値 \( M \) を取ります。
以上より、連続関数 \( f \) は閉区間 \( I \) 上で最大値を持つことが示されました。同様の議論で最小値の存在も示せるため、最大値・最小値の定理が証明されました。