階乗の定義・計算方法・性質・練習問題について
1. 階乗とは？
階乗 (factorial) とは、ある自然数 n に対して、その数から 1 までのすべての自然数を掛け合わせた値のことを指します。数学では、階乗を \( n! \) と表記します。この記号は、「n の階乗」と読みます。
1.1. 階乗の定義
\[ n! = n \times (n-1) \times (n-2) \times \cdots \times 3 \times 2 \times 1 = \prod_{k=1}^{n} k \]
また、階乗は再帰的に定義することもできます。この場合、次の関係式が成り立ちます。
\[ n! = n \times (n-1)! \]
特に、ゼロの階乗 \( 0! \) は特別な定義として 1 になります。
\[ 0! = 1 \]
階乗はガンマ関数と深い関係があります。
1.2. 階乗の計算例
\( 6! = 6 \times 5 \times 4 \times 3 \times 2 \times 1 = 720 \)
\( 5! = 5 \times 4 \times 3 \times 2 \times 1 = 120 \)
\( 4! = 4 \times 3 \times 2 \times 1 = 24 \)
\( 3! = 3 \times 2 \times 1 = 6 \)
\( 2! = 2 \times 1 = 2 \)
\( 1! = 1 \)
さらに、先ほど述べたように、ゼロの階乗は次のように定義されます。
\( 0! = 1 \)
1.3. 爆発的に増える
階乗の計算はグラフをのようにnが増えるごとに爆発的に増えます。
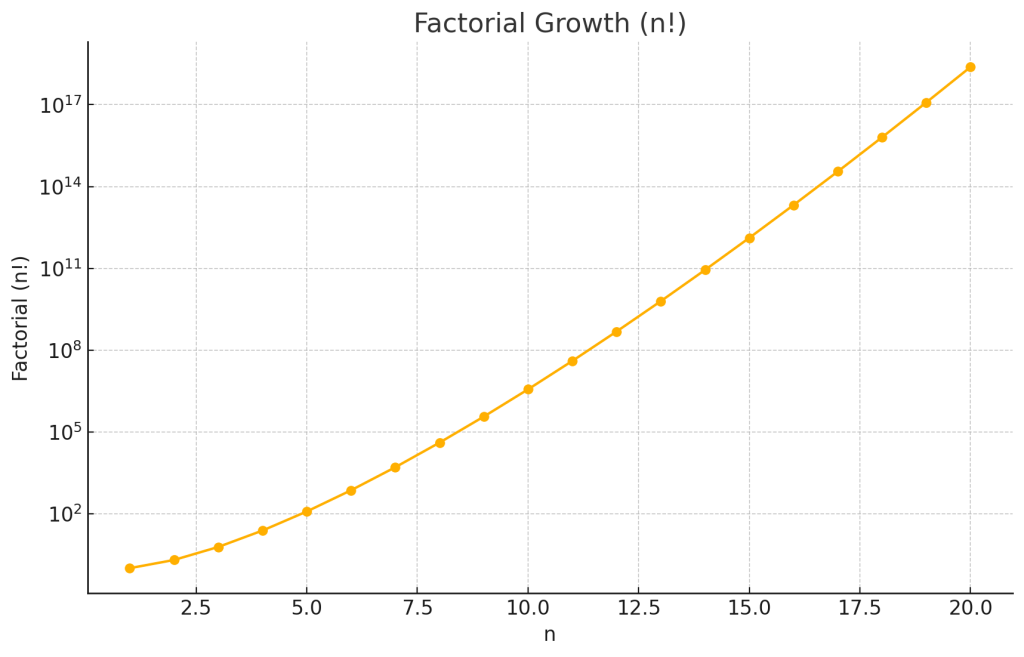縦軸に注目すると、4!までは$10^2$以下でしたが、$20!$では$10^{17}$を超えるという事態になっています。
さらに、スターリングの近似（Stirling’s approximation）という公式を使うと、大きな \( n \) に対して階乗がどれほど大きくなるかを評価できます。
\[ n! \approx \sqrt{2\pi n} \left(\frac{n}{e}\right)^n \]
2. 階乗を利用した場合の数の例題
2.1. 例題 1: 猫の並べ方
全員が異なる順番で並ぶ方法の数は、6人の階乗 \( 6! \) で求めることができます。
\[ 6! = 6 \times 5 \times 4 \times 3 \times 2 \times 1 = 720 \]
したがって、6人が一列に並ぶ方法は 720 通りあります。
階乗を利用した場合の数の例題をいくつか作成しました。
2.2. 例題 2: クラスの席替え
10人の生徒が並ぶ順列の数は、10人全員の階乗で表されます。 したがって、求める場合の数は \( 10! \) です。
計算すると、 \[ 10! = 10 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1 = 3,628,800 \] したがって、席替えの並び方の総数は 3,628,800通り です。
2.3. 例題 3: 文字の並び替え
4つの文字を並び替える順列の数は、4文字全ての階乗で表されます。 したがって、求める場合の数は \( 4! \) です。
計算すると、 \[ 4! = 4 \times 3 \times 2 \times 1 = 24 \] したがって、異なる文字列の総数は24通りです。
