フェルマー数の定義・性質・具体例・漸化式について

1. フェルマー数とは

ここで、\(n\) は0以上の整数です。フェルマー数の名前は、フランスの数学者ピエール・ド・フェルマー（Pierre de Fermat）に由来しています。

1.1. フェルマー数の具体例

例えば、最初のいくつかのフェルマー数は以下のようになります。

• \( F_0 = 2^{2^0} + 1 = 2^1 + 1 = 3 \)
• \( F_1 = 2^{2^1} + 1 = 2^2 + 1 = 5 \)
• \( F_2 = 2^{2^2} + 1 = 2^4 + 1 = 17 \)
• \( F_3 = 2^{2^3} + 1 = 2^8 + 1 = 257 \)
• \( F_4 = 2^{2^4} + 1 = 2^{16} + 1 = 65537 \)

フェルマー数にはいくつかの興味深い特徴があります。フェルマーは、すべてのフェルマー数が素数であると予想されましたが、この予想は誤りであることが後に判明しました。最初のいくつかのフェルマー数は素数ですが、\(F_5 = 2^{32} + 1\) は素数ではありません。この数は 641、6700417, 4294967297で割り切れることが知られています。

2. フェルマー数の性質

2.1. フェルマー数の漸化式1

フェルマー数の一般式を再確認すると、

\[ F_n = 2^{2^n} + 1 \]

です。次のフェルマー数 \(F_{n+1}\) は、

\[ F_{n+1} = 2^{2^{n+1}} + 1 = 2^{2 \cdot 2^n} + 1 = (2^{2^n})^2 + 1 \]

一方で、\(2^{2^n}\) は次のようになります。

\[ F_n – 1 = 2^{2^n} \]

これを用いると、

\[ F_{n+1} = (F_n – 1)^2 + 1 \]

2.2. フェルマー数の漸化式2

$F_n(F_n-2)$の積を計算します。

$$F_n(F_n-2)= (2^{2^n}+1)(2^{2^n}-1)$$

$$=2^{2^n+2^n}-1$$

$$=2^{2^{n+1}}-1$$

$$=F_{n+1}-2$$

色の付けた部分の漸化式について着目する。

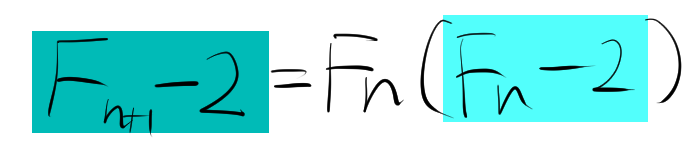色の付けた部分は添え字が1違うだけなので、次のようになります。

$$F_{n+1}-2=F_n(F_n-2)$$

$$=F_nF_{n-1}(F_{n-1}-2)$$

$$=F_nF_{n-1}F_{n-2}(F_{n-2}-2)$$

$$=F_nF_{n-1}F_{n-2}\dots F_0(F_{0}-2)$$

$$=F_nF_{n-1}F_{n-2}\dots F_0$$

$$= \prod^n_{k=0}F_k$$

したがって、

\[ F_{n+1} = \prod^n_{k=0}F_k+2 \]

2.3. フェルマー数は互いに素

フェルマー数 \( F_n = 2^{2^n} + 1 \) が互いに素であることを背理法で示します。

フェルマー数 \( F_n \) と \( F_m \)（\( n < m \)）が互いに素でない、つまり共通の素因数 \( p \) を持つと仮定します。

フェルマー数の一般式 \( F_{n+1} = \prod_{k=0}^{n} F_k + 2 \) を利用します。この式は示した漸化式より、次のように解釈できます。

\[ F_{n+1} = F_0 \times F_1 \times \cdots \times F_n + 2 \]

ここで、$m=n+1$のとき、仮定によれば \( F_n \) と \( F_m \)（\( n < m \)）は共通の素因数 \( p \) を持ちます。

\( F_{n+1} = F_0 \times F_1 \times \cdots \times F_n + 2 \) を見ると、\( F_{n+1} \) は \( F_0 \) から \( F_n \) までの積に 2 を加えたものです。

このとき、 \( F_0 \times F_1 \times \cdots \times F_n \) と$F_{n+1}$はpで割り切れます。

p=2となるが、フェルマー数は「偶数+1」になっているため、必ず奇数になることに矛盾する。

したがって、フェルマー数はすべて互いに素であることが示されました。