
はるか
フィボナッチ数列の漸化式、
fn=fn−1+fn−2、シンプル。

ふゅか
そうそう!最初はゼロから始まって、どんどん数が増えていくのが面白いわよね。
1. フィボナッチ数列の漸化式
f0=0、
f1=1としたとき、フィボナッチ数列は、以下の漸化式によって定義されます。
fn=fn−1+fn−2(n≥2)
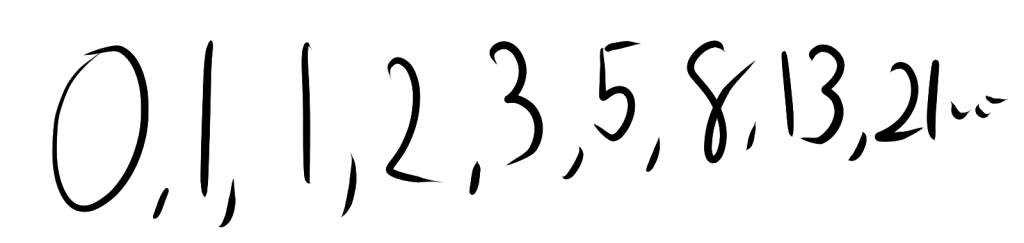
2. 一般項
フィボナッチ数列の一般項は以下のようになります。
fn=51{(21+5)n−(21−5)n}
2.1. 一般項の求め方
x2−x−1=0の解は21±5であることから、大きいほうの解をα、小さいほうの解をβとおく。以下の漸化式に変形することができる。
fn+2−αfn+1=β(fn+1−αfn)
fn+2−βfn+1=α(fn+1−βfn)
それぞれ、{fn+2−αfn+1}公比がβの等比数列、{fn+2−βfn+1}公比がαの等比数列である。したがって、
fn+1−αfn=βn(f1−αf0)
∴fn+1−αfn=βn・・・①
fn+1−αfn=αn(f1−βf0)
∴fn+1−βfn=αn・・・②
よって、②-①をすると、α−β=5より、
(α−β)fn=αn−βn
fn=α−βαn−βn
∴fn=51{(21+5)n−(21−5)n}
3. フィボナッチ数列の性質

はるか
フィボナッチ数列の性質、面白い。加法定理みたいな漸化式が出てくる。

ふゅか
まさに!
fm+n=fm+1fn+fmfn−1っていう式を使うと、いろんなフィボナッチ数がつながるんだね!これ、数学的帰納法で証明もできるのが素敵☆
3.1. 加法定理みたいな漸化式
フィボナッチ数列の第
m+n項を、別の項から求めることができます。具体的には、任意の非負整数
m,任意の自然数
nについて、以下の式が成り立ちます。
fm+n=fm+1fn+fmfn−1
3.1.1. 数学的帰納法を利用した証明
数学的帰納法を利用して証明します。
[1]n=1のときは、左辺はfm+1、右辺はfm+1f1+fmf0=fm+1となり、両辺が等しいことがわかります。
[2]n=2のときは、左辺はfm+2、右辺はfm+1f2+fmf1=fm+1+fm=fm+2となり、両辺が等しいことがわかります。
さらに、n=k、n=k−1のとき
fm+k=fm+1fk+fmfk−1
fm+k−1=fm+1fk−1+fmfk−2
式が成り立つと仮定する。
[3]n=k+1のとき、左辺はfm+k+1、右辺はfm+1fk+1+fmfkです。ここで、フィボナッチ数列の漸化式を用いると、fk+1=fk+fk−1、fk=fk−1+fk−2、fm+k=fk+1fm+fkfm−1が成り立つため、右辺を以下のように変形することができます。
fm+1fk+1+fmfk
=fm+1(fk+fk−1)+fm(fk−1+fk−2)
=fm+1fk+fm+1fk−1+fmfk−1+fmfk−2
ここで、仮定より、fm+k=fm+1fk+fmfk−1とfm+k−1=fm+1fk−1+fmfk−2が成り立つため、
fm+1fk+fm+1fk−1+fmfk−1+fmfk−2
=fm+1fk+fmfk−1+fm+1fk−1+fmfk−2
=fm+k+fm+k−1
フィボナッチ数列の漸化式より、fm+k+1=fm+k+fm+k−1であるから、
=fm+k+fm+k−1
=fm+k+1
よって、右辺と左辺が等しいため、n=k+1のときも成り立つ。
数学的帰納法により、fm+k=fm+1fk+fmfk−1は成り立つ。
3.1.2. 一般項を用いた証明
fn=α−βαn−βnを用いて証明を行う。
fm+1fn+fmfn−1
=(α−β)2(αm+1−βm+1)(αn−βn)+(α−β)2(αm−βm)(αn−1−βn−1)
=(α−β)2αm+n+1−αm+1βn−αnβm+1+βm+n+1+αm+n−1−αmβn−1−αn−1βm+βm+n−1
x2−x−1=0の解は21±5であるため、解と係数の関係より、α+β=1、αβ=−1である。
αβ=−1より、
αm+1βn=−αmβn−1
αnβm+1=−αn−1βm
であことと、α=−β1、β=−α1より、
=(α−β)2αm+n+1+βm+n+1+αm+n−1+βm+n−1
=(α−β)2αm+n(α+α1)+βm+n(β+β1)
=(α−β)2αm+n(α−β)−βm+n(α−β)
=α−βαm+n−βm+n
=fm+n
となる。よって、fm+n=fm+1fn+fmfn−1である。
3.2. 連続する2つのフィボナッチ数列の数の平方の和の漸化式
連続するフィボナッチ数列の数の平方の和はフィボナッチ数になる。
たとえば、f5=5、f6=8であるから、
f52+f62
=25+64
=89
=f11
とのように、f52とf62の和はf11になります。
証明は先ほどの漸化式を用いれば簡単に求めることができます。m=n−1のとき、
fm+n=fm+1fn+fmfn−1
f2n−1=fnfn+fn−1fn−1
∴f2n−1=fn2+fn−12
よって、n=6のときに、先ほど示した例のようになります。

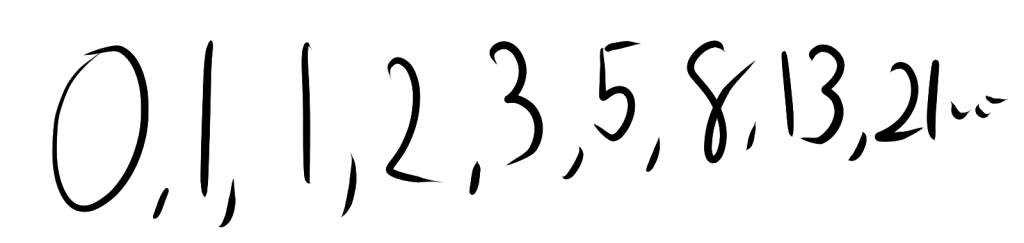

-e1727156598416.png.webp)


