三角形の五心の一覧について

はるか
五心について勉強しよう。
ふゅか
いいわね!五心は三角形の重要なポイントよね!
1. 三角形の五心とは
三角形には、「五心」と呼ばれる特別な五つの点が存在します。ここでは、五心である「重心」「外心」「内心」「垂心」「傍心」についてわかりやすくまとめていきます。
2. 重心
ふゅか
重心は中線の交点なのよね!
はるか
中線は辺の中点と頂点を結ぶ線。
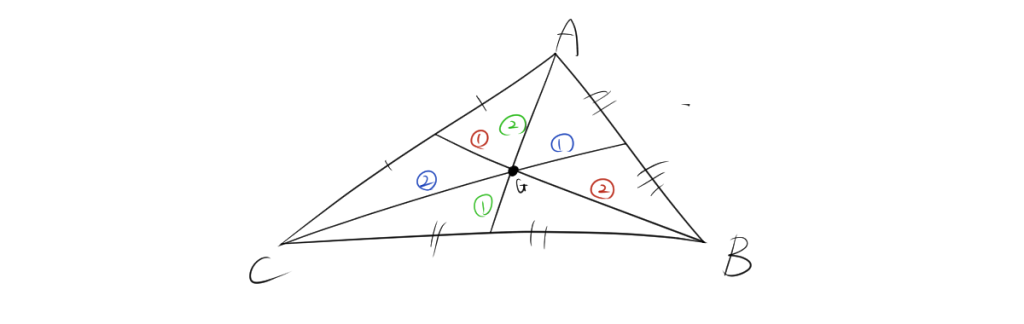
重心は、三角形の3つの頂点からそれぞれ対辺に引いた中線の交点です。中線とは、三角形の各辺の中点を結ぶ線で、どの頂点からでも2:1の比率で中線を分ける特性を持っています。
2.1. 重心の特徴
- 三角形の内部に常に存在する。
- 物理的には三角形を支える点となる。
- 2:1の比率で中線を分ける
3. 外心
ふゅか
次は外心ね!外心は外接円の中心になるのよね。
はるか
辺の垂直二等分線の交点。
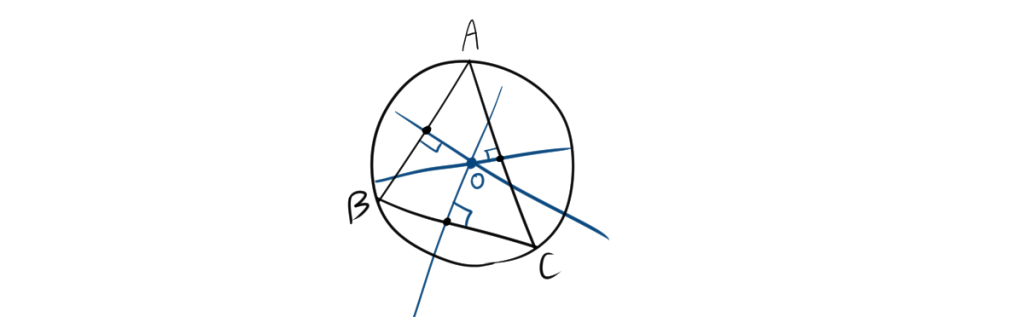
外心は、三角形の各辺の垂直二等分線の交点です。この点は、三角形の外接円(すべての頂点を通る円)の中心となります。
3.1. 外心の特徴
- 外接円の中心になる。
- 各頂点からの距離が等しい。$OA=OB=OC$
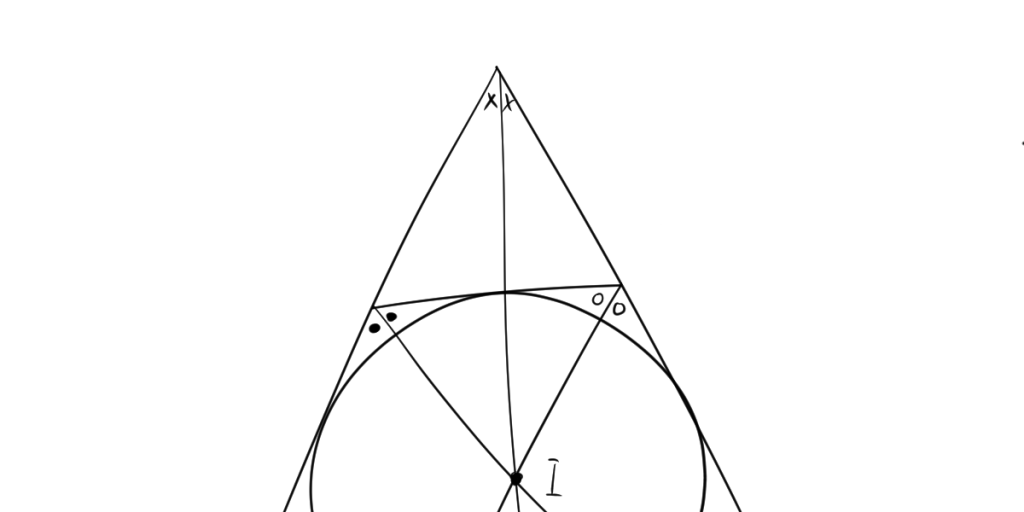
4. 内心
ふゅか
内心は内接円の中心ね!三角形の内角の二等分線の交点よ。
はるか
各辺からの距離が等しい。
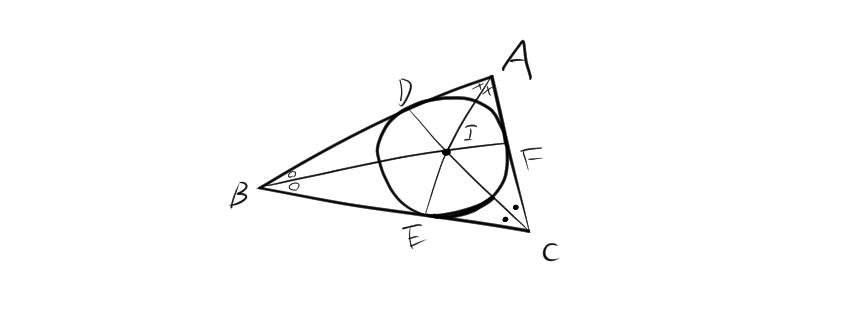
内心は、三角形の内角の二等分線の交点であり、三角形の内接円(すべての辺に接する円)の中心です。
4.1. 内心の特徴
- 内接円の中心になる。
- 内接円の半径は等しいため、$ID=IE=IF$
5. 垂心
ふゅか
垂心は垂線の交点ね。頂点から対辺に引いた垂線の交点よ。
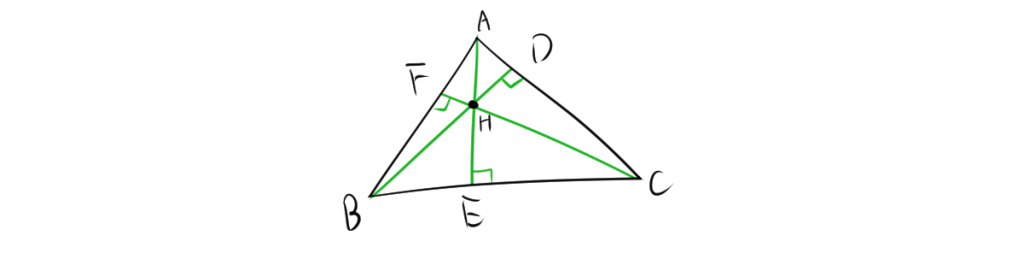
垂心は、三角形の3つの頂点から対辺に引いた垂線の交点です。垂線は、各頂点から対向する辺に垂直に引かれた線です。
5.1. 垂心の特徴
- 外接円の半径をRとすると、$AH=2R\cos A$
6. 傍心
傍心は、三角形の一つの内角の二等分線と、他の二つの辺の外角の二等分線の交点で、三角形の傍接円(三角形の1辺に接し、他の2辺を延長したものに接する円)の中心です。
PR