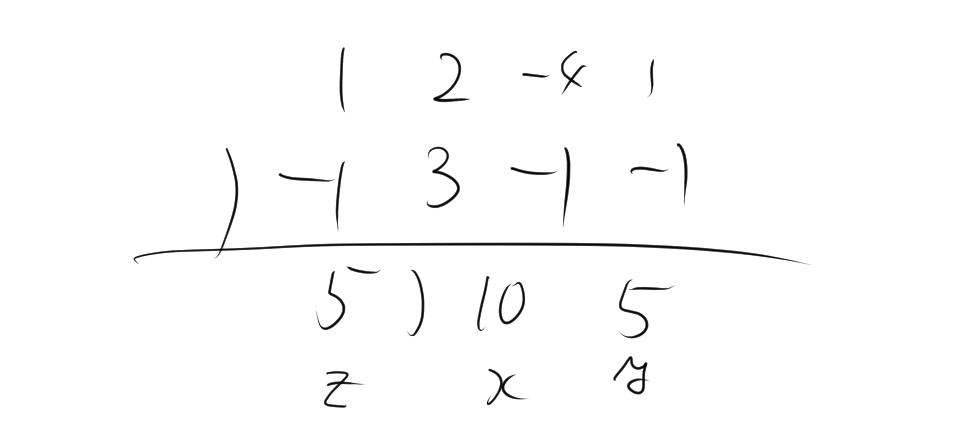ベクトルと平面の方程式とは?法線ベクトルと例題について

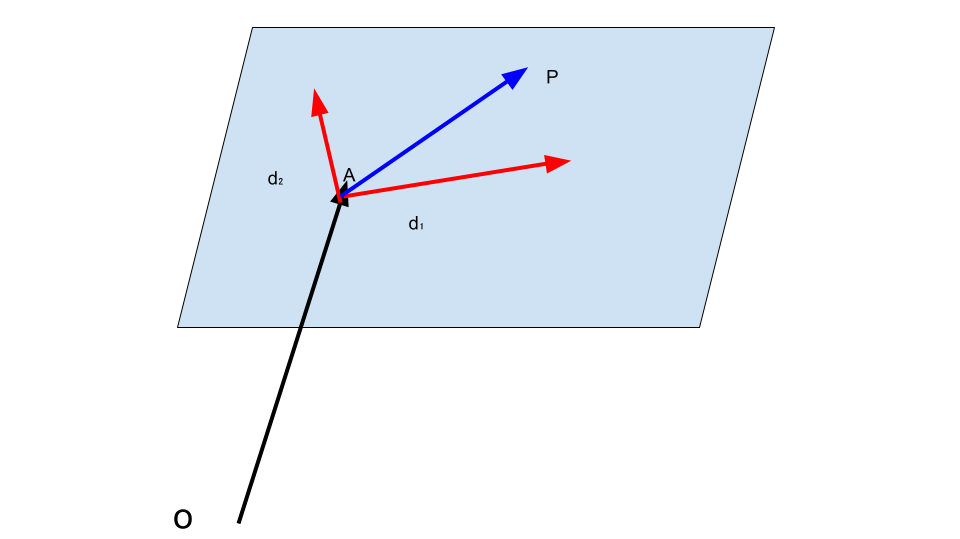
1. 平面のベクトル方程式
$$\boldsymbol{p}=\boldsymbol{a}+s\boldsymbol{d_1}+t\boldsymbol{d_2}$$
$\boldsymbol{d_1}$,$\boldsymbol{d_2}$は方向ベクトルとする。
2. 法線ベクトルと平面の方程式
$$ax+by+cz+d=0$$
2.1. 平面の方程式を求める
$\boldsymbol{p}=(x,y,z)$ 平面αと垂直なベクトル(法線ベクトル)$\boldsymbol{n}=(a,b,c)$ $ \boldsymbol{a}=(x_1,y_1,z_1)$とする。
$\vec{AP}=\boldsymbol{p}-\boldsymbol{a}$、$\vec{AP}\cdot \boldsymbol{n}=0$より、
$(\boldsymbol{p}-\boldsymbol{a})\cdot\boldsymbol{n}=0$
$\boldsymbol{p}-\boldsymbol{a}=(x-x_1,y-y_1,z-z_1)$より、法線ベクトルとの内積を計算すると、
$a(x-x_1)+b(y-y_1)+c(z-z_1)=0$
となる。$d=-(ax_1+by_1+cz_1)$と置くと、
$ax+by+cz+d=0$となる。
法線ベクトルは平面と直角であるので、方向ベクトルの外積で求めることができる。
3. 例題
3.1. 例題1: 法線ベクトルと平面の方程式の求め方
点 \( A, B, C \) を通る平面の法線ベクトルを求めるために、まずベクトル \( \overrightarrow{AB} \) とベクトル \( \overrightarrow{AC} \) を求めます。
\[ \overrightarrow{AB} = (2 – 1, 0 – (-2), -1 – 3) = (1, 2, -4) \]
\[ \overrightarrow{AC} = (0 – 1, 1 – (-2), 2 – 3) = (-1, 3, -1) \]
法線ベクトルは、ベクトル \( \overrightarrow{AB} \) とベクトル \( \overrightarrow{AC} \) の外積で求めます。
\[ \overrightarrow{n} = \overrightarrow{AB} \times \overrightarrow{AC}= (10, 5, 5) \]
よって、法線ベクトルは \( \overrightarrow{n} = (10, 5, 5) \) です。平面の方程式は、点 \( A(1, -2, 3) \) を使うと、
\[ 10(x – 1) + 5(y + 2) + 5(z – 3) = 0 \]
展開して整理すると、
\[ 10x + 5y + 5z – 10 + 10 – 15 = 0 \]
\[ 10x + 5y + 5z – 15 = 0 \]
よって、平面の方程式は
\[ 10x + 5y + 5z = 15 \]
です。
3.2. 例題2
点 \( P(3, -1, 2) \) を使うと、
\[ 2(x – 3) – 1(y + 1) + 4(z – 2) = 0 \]
展開して整理すると、
\[ 2x – 6 – y – 1 + 4z – 8 = 0 \]
\[ 2x – y + 4z – 15 = 0 \]
よって、平面の方程式は
\[ 2x – y + 4z = 15 \]
平面の方程式が \( 2x – y + 4z – 15 = 0 \) のとき、点 \( (x_1, y_1, z_1) \) から平面までの距離 \( d \) は次の公式で求められます。
\[ d = \frac{|ax_1 + by_1 + cz_1 + d|}{\sqrt{a^2 + b^2 + c^2}} \]
したがって、
$$\begin{align*} d &= \frac{|2 \cdot 1 – 1 \cdot 2 + 4 \cdot (-1) – 15|}{\sqrt{2^2 + (-1)^2 + 4^2}} \\ &= \frac{|2 – 2 – 4 – 15|}{\sqrt{4 + 1 + 16}} \\ &= \frac{|-19|}{\sqrt{21}} \\ &= \frac{19}{\sqrt{21}} \\ &= \frac{19\sqrt{21}}{21} \end{align*}$$
よって、点 \( Q(1, 2, -1) \) から平面までの距離は \( \frac{19\sqrt{21}}{21} \) です。