床関数(ガウス記号)と天井関数の性質・具体例について

1. 床関数と天井関数
床関数 (floor function) と天井関数 (ceiling function) は、実数を整数に変換する際によく使われる関数です。それぞれ次のように定義されます。
1.1. 床関数
床関数 \( \lfloor x \rfloor \) は、実数 \( x \) をそれ以下の最大の整数に変換します。
例えば、
- \( \lfloor 3.7 \rfloor = 3 \)
- \( \lfloor -2.3 \rfloor = -3 \)
このように、常に \( x \) 以下の最大の整数が選ばれます。また、床関数は次のように書かれることがあります。
- $\text {floor} (x)$
- $[x]$
$[x]$は特に、ガウス記号と呼ばれます。
$$\displaystyle \lfloor x\rfloor =\max\{n\in \mathbb {Z} \mid n\leq x\}$$
床関数の写像 は
$$\lceil \cdot \rceil : \mathbb{R} \to \mathbb{Z}$$
$$[\cdot] : \mathbb{R} \to \mathbb{Z}$$
$$\text{floor} : \mathbb{R} \to \mathbb{Z}$$
1.2. 天井関数
天井関数 \( \lceil x \rceil \) は、実数 \( x \) をそれ以上の最小の整数に変換します。
例えば、
- \( \lceil 3.7 \rceil = 4 \)
- \( \lceil -2.3 \rceil = -2 \)
天井関数は常に \( x \) 以上の最小の整数を返します。また、天井関数は次のように書かれることがあります。
- ${\displaystyle \text{ceil} (x)}$
- ${\displaystyle \text{ceiling} (x)}$
$$\displaystyle \lceil x\rceil =\min\{n\in \mathbb {Z} \mid x\leq n\}$$
天井関数の写像 は
$$\lceil \cdot \rceil : \mathbb{R} \to \mathbb{Z}$$
$$\text{ceil} : \mathbb{R} \to \mathbb{Z}$$
$$\text{ceiling} : \mathbb{R} \to \mathbb{Z}$$
1.3. 例
もし \( x = 2.8 \) であれば
- \( \lfloor 2.8 \rfloor = 2 \)
- \( \lceil 2.8 \rceil = 3 \)
また、\( x = -2.8 \) であれば
- \( \lfloor -2.8 \rfloor = -3 \)
- \( \lceil -2.8 \rceil = -2 \)
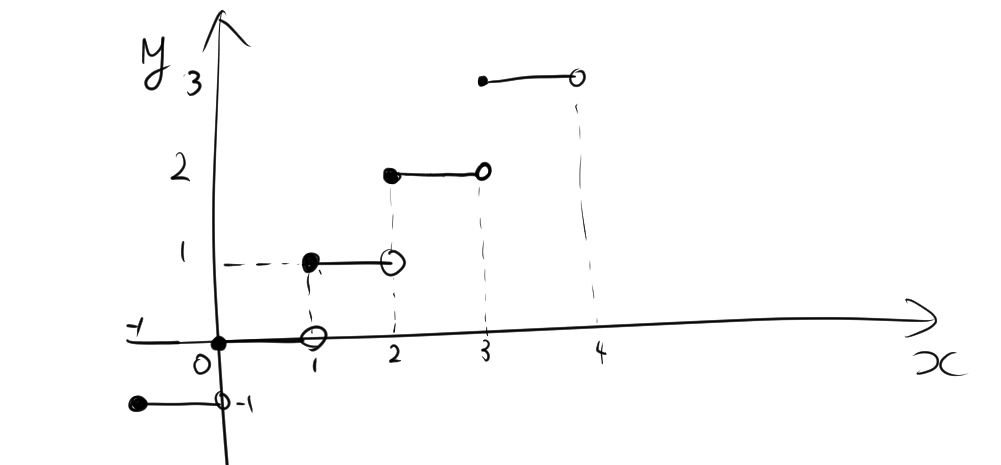
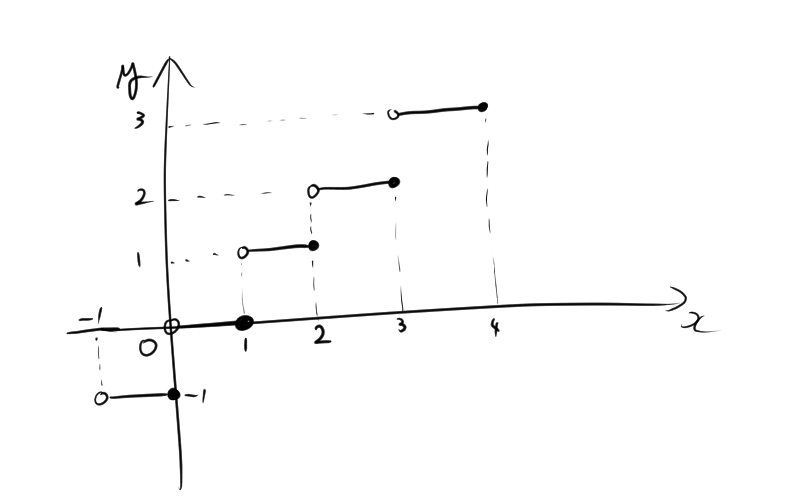
2. 床関数と天井関数のグラフ
床関数をグラフにすると、
3. 床関数と天井関数の性質
3.1. 床関数と天井関数の不等式
$$\displaystyle \lceil x\rceil -1<x\leq \lceil x\rceil $$
\( \lfloor x \rfloor \leq x < \lfloor x \rfloor + 1 \)を証明します。
まず、\(\lfloor x \rfloor\) は \(x\) を超えない最大の整数であるから次が成り立ちます。
\[ \lfloor x \rfloor \leq x \]
次に、\(\lfloor x \rfloor\) は \(x\) を超えない最大の整数なので、\(\lfloor x \rfloor + 1\) は \(x\) よりも大きな最小の整数となります。したがって、次が成り立ちます。
\[ x < \lfloor x \rfloor + 1 \]
以上より、次の不等式が成り立つことがわかります。
\[ \lfloor x \rfloor \leq x < \lfloor x \rfloor + 1 \]
\( \lceil x \rceil – 1 < x \leq \lceil x \rceil \)を証明します。
次に、\(\lceil x \rceil\) は \(x\) 以上の最小の整数から、次が成り立ちます。
\[ x \leq \lceil x \rceil \]
さらに、\(\lceil x \rceil – 1\) は \(x\) より小さな最大の整数なので、次が成り立ちます。
\[ \lceil x \rceil – 1 < x \]
したがって、次の不等式が成り立つことがわかります。
\[ \lceil x \rceil – 1 < x \leq \lceil x \rceil \]
3.2. 床関数と天井関数の関係
\(-x\) に対して \(\lfloor -x \rfloor\) を考えると、\(-x\) より小さいか等しい最大の整数が \(\lfloor -x \rfloor\) です。
このとき、\(\lfloor -x \rfloor \leq -x < \lfloor -x \rfloor + 1\) となります。
両辺にマイナスをかけると、
\[ -\lfloor -x \rfloor – 1 < x \leq -\lfloor -x \rfloor \]
となります。ここで、天井関数は次の不等式が成り立つので、
\[ \lceil x \rceil – 1 < x \leq \lceil x \rceil \]
したがって、\(\lceil x \rceil = -\lfloor -x \rfloor\) が成立します。
3.3. 床関数と天井関数の和
\( n \) が偶数の場合
\( n \) が偶数であると仮定すると、\( n = 2k \) と書けます(ここで \( k \) は整数です)。このとき、\(\frac{n}{2} = k\) なので、
$$ \left\lfloor \frac{n}{2} \right\rfloor = k \quad \text{および} \quad \left\lceil \frac{n}{2} \right\rceil = k $$
したがって、
$$ \left\lfloor \frac{n}{2} \right\rfloor + \left\lceil \frac{n}{2} \right\rceil = k + k = 2k = n $$
偶数の場合、式は成り立ちます。
\( n \) が奇数の場合
\( n \) が奇数であると仮定すると、\( n = 2k + 1 \) と書けます(ここで \( k \) は整数です)。このとき、\(\frac{n}{2} = k + \frac{1}{2}\) なので、
$$ \left\lfloor \frac{n}{2} \right\rfloor = k \quad \text{および} \quad \left\lceil \frac{n}{2} \right\rceil = k + 1 $$
したがって、
$$ \left\lfloor \frac{n}{2} \right\rfloor + \left\lceil \frac{n}{2} \right\rceil = k + (k + 1) = 2k + 1 = n $$
奇数の場合も、式は成り立ちます。
したがって、任意の整数 \(n\) に対して、
$$ \left\lfloor \frac{n}{2} \right\rfloor + \left\lceil \frac{n}{2} \right\rceil = n $$
が成り立つことが示されました。