【論理回路】全加算器の回路図と真理値表、動作、意味について

1. 加算器
そもそも、加算器(かさんき、Adder)は、足し算を行うためのデジタル回路です。コンピューターや電子計算機において、算術演算の基本要素として非常に重要な役割を果たします。
2. 全加算器とは?
全加算器(ぜんかさんき、Full Adder)とは、3つの入力(2つのデータ入力と1つの繰り上がり入力)から2つの出力(合計と繰り上がり)を得る論理回路です。主にビット単位での加算を行う際に使用され、複数の全加算器を組み合わせることで、多ビットの加算が可能になります。
2.1. 全加算器の必要性
コンピュータは二進数(0と1)でデータを処理します。数値を加算する際、各ビットの計算と繰り上がりの処理が必要です。全加算器はこの繰り上がりの処理を含めたビット加算を実現します。
2.2. 全加算器の構成
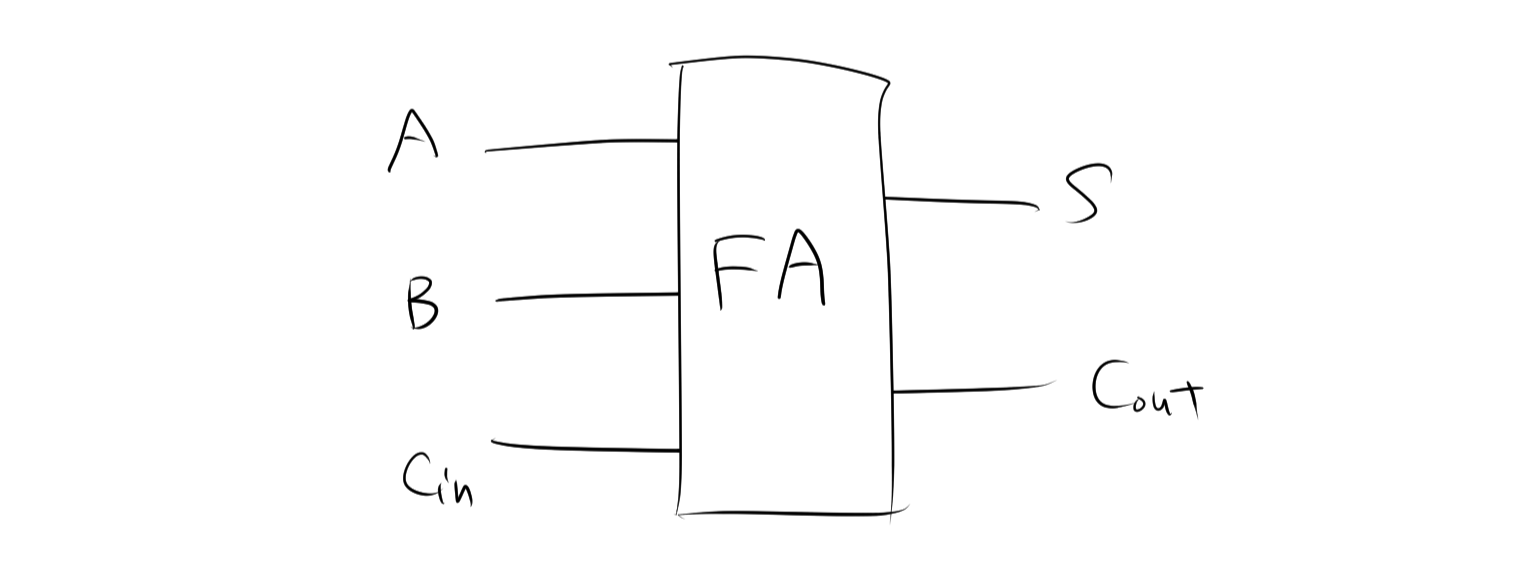
次のような長方形で全加算器を表します。
3. 真理値表で見る全加算器
入力A、入力B、および繰り上げ入力 ($C_{in}$) を用いて和 (S) を計算し、必要であれば繰り上がり出力 ($C_{out}$) を出力する真理値表を書くと次のようになります。
| 入力A (A) | 入力B (B) | 繰り上がり入力 (Cin) | 合計出力 (S) | 繰り上がり出力 (Cout) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
4. 全加算器の論理式
4.1. Sの論理式の導出
以下の表は、三つの入力信号$A,B,C_{in}$から、信号Sの出力が1になる真理値表です。この表をもとに、出力 $S$の論理式を導きます。
| A | B | Cin | S |
|---|---|---|---|
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 |
出力$S$は次のようになります。
\[ \begin{align*} S &= (\overline{A} \cdot \overline{B} \cdot C_{in}) + (\overline{A} \cdot B \cdot \overline{C_{in}}) + (A \cdot \overline{B} \cdot \overline{C_{in}}) + (A \cdot B \cdot C_{in}) \\ & = (\overline{A} \cdot \overline{B}+A \cdot B)C_{in}+(\overline{A} \cdot B+A \cdot \overline{B} )\overline{C_{in}} \end{align*} \]
ここで、$ T= \overline{A} \cdot \overline{B}+A \cdot B$とすると
$$\overline T = \overline{A} \cdot \overline{B}+A \cdot B$$
となるので、
\[ \begin{align*} S &=(\overline{A} \cdot \overline{B}+A \cdot B)C_{in}+(\overline{A} \cdot B+A \cdot \overline{B} )\overline{C_{in}} \\ & = \overline T\cdot C_{in}+T \cdot \overline{C_{in}} \\ & =T \oplus C_{in} \\ & =( \overline{A} \cdot \overline{B}+A \cdot B ) \oplus C_{in} \\ &= ( A \oplus B ) \oplus C_{in} \end{align*} \]
4.2. $C_{out}$の論理式
以下の表は、三つの入力信号$A,B,C_{in}$から、信号$C_{out}$の出力が1になる真理値表です。この表をもとに、出力 $C_{out}$の論理式を導きます。
| A | B | Cin | Cout |
|---|---|---|---|
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
次に、桁上げ出力(キャリーアウト)の論理式を導きます。
\[ \begin{align*} C_{\text{out}} &= (\overline{A} \cdot B \cdot C_{\text{in}}) + (A \cdot \overline{B} \cdot C_{\text{in}}) + (A \cdot B \cdot \overline{C_{\text{in}}}) + (A \cdot B \cdot C_{\text{in}}) \\ &= (\overline{A} \cdot B + A \cdot \overline{B}) \cdot C_{\text{in}} + A \cdot B \cdot (C_{\text{in}} + \overline{C_{\text{in}}}) \\ &= (A \oplus B) \cdot C_{\text{in}} + A \cdot B \end{align*} \]
5. 回路図の作成
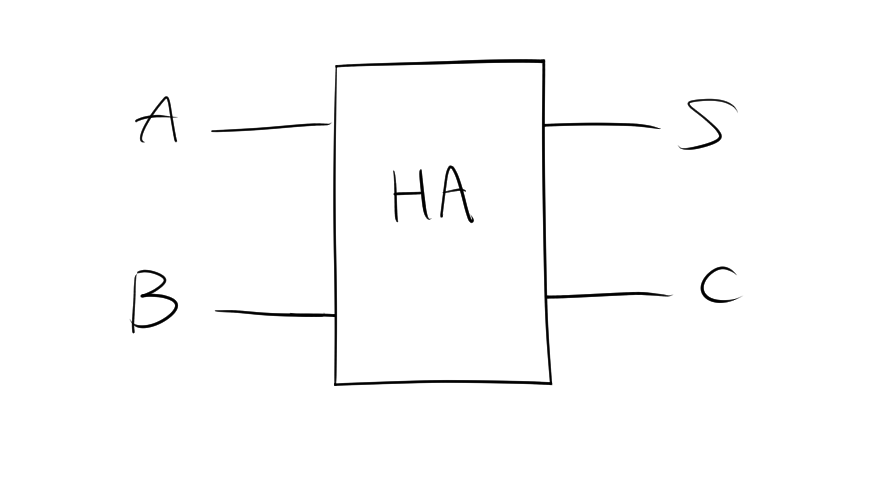
5.1. 半加算器
全加算器の回路図を書くために、半加算器を利用する。
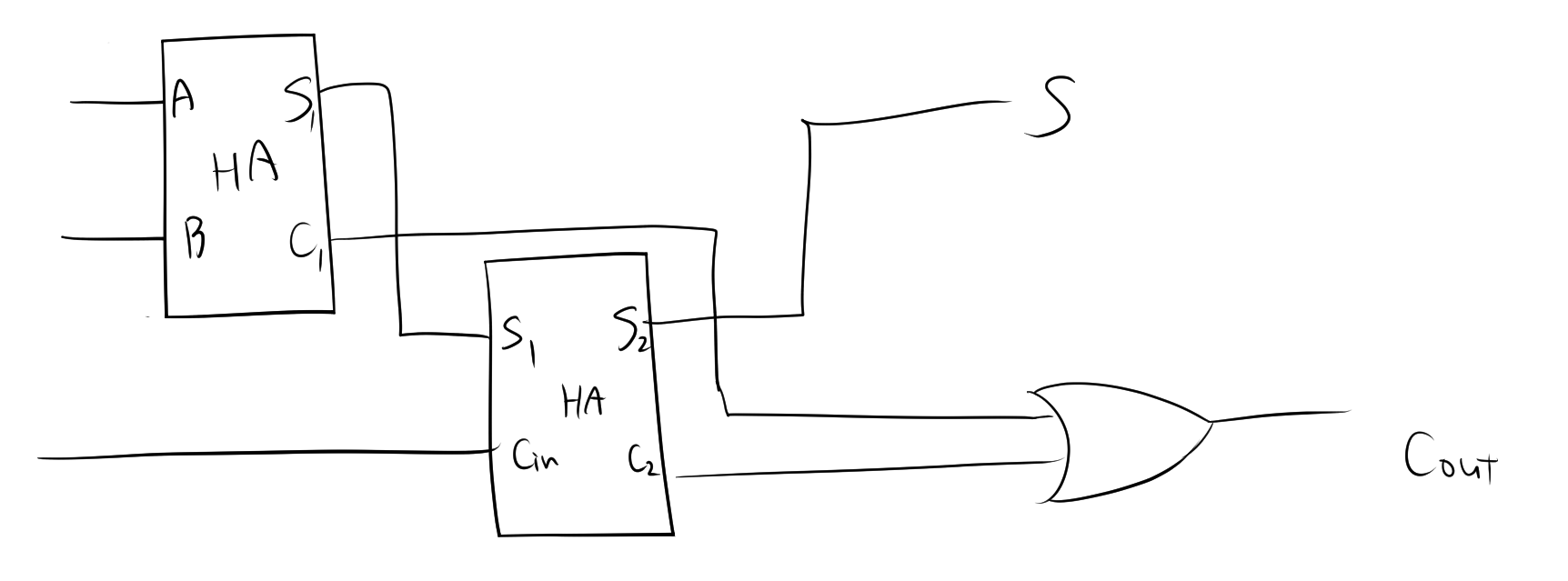
5.2. 全加算器
したがって、全加算器は、以下のように半加算器で構成することができます。