三角形の重心の位置ベクトルとは？導出と例題について

はるか

三角形の重心は、3つの頂点の位置ベクトルの平均で求まる。

ふゅか

うん、そうね！重心は三角形全体のバランスを取る点だよね♪

1. 三角形の重心

1.1. 重心のベクトルの導出

次のような三角形ABCを考えます。Mは中点、Gは重心として、重心の性質より$AG:GM=2:1$になります。

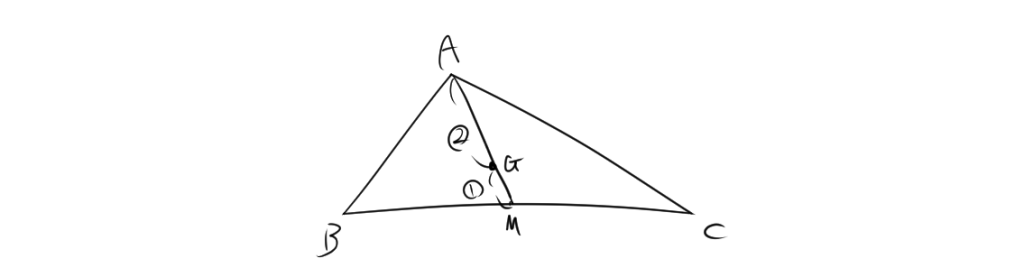点\(\mathbf{A}\)、\(\mathbf{B}\)、\(\mathbf{C}\) 、\(\mathbf{G}\) 、\(\mathbf{M}\) とし、それぞれの位置ベクトルを \(\vec{a}\)、\(\vec{b}\)、\(\vec{c}\) 、\(\vec{g}\) 、\(\mathbf{A}\)0とします。 \(\mathbf{A}\)0は

$$\begin{align*} \vec{m} &= \overrightarrow{OB} + \overrightarrow{BM} \\ &= \vec{b} + \overrightarrow{BM} \end{align*}$$

ここで、中点の性質より$\overrightarrow{BM}=\frac{1}{2}{\overrightarrow {BC}}$であるため、

$$\begin{align*} &= \vec{b} + \frac{1}{2} \overrightarrow{BC} \\ &= \vec{b} + \frac{1}{2} (\vec{c} – \vec{b}) \\ &= \frac{\vec{b} + \vec{c}}{2} \end{align*}$$

中線 \(AM\) 上に重心 \(G\) があり、重心は中線を \(2:1\) に内分します。そのため、重心 \(G\) の位置ベクトルは内分点の位置ベクトルより、次のように表せます。

\[ \vec{g} = \frac{2\vec{m} + \vec{a}}{3} \]

\(\vec{m}\) を代入すると

\[ \vec{g} = \frac{2 \cdot \frac{\vec{b} + \vec{c}}{2} + \vec{a}}{3} \]

したがって、

\[ \vec{g} = \frac{\vec{a} + \vec{b} + \vec{c}}{3} \]

ふゅか

重心は中線を\(2:1\)に内分する性質も持ってるよね。

はるか

うん。その性質から、内分点の位置ベクトルの公式を利用する。

2. 例題

2.1. 例題1

まず、各頂点の位置ベクトルを \(\vec{a} = (1, 2)\)、\(\vec{b} = (3, 8)\)、\(\vec{c} = (-1, 4)\) とします。重心の位置ベクトル \(\vec{g}\) は次のように求められます。

\[ \begin{align*} \vec{g} &= \frac{\vec{a} + \vec{b} + \vec{c}}{3} \\ &= \frac{(1, 2) + (3, 8) + (-1, 4)}{3} \\ &= \frac{(1 + 3 – 1, 2 + 8 + 4)}{3} \\ &= \left( \frac{3}{3}, \frac{14}{3} \right) \\ &= \left( 1, \frac{14}{3} \right) \end{align*} \]

したがって、重心の位置ベクトルは \((1, \frac{14}{3})\) です。

2.2. 例題2

重心の位置ベクトルより、

\[ (100, 100) = \frac{(1, 1) + (99, 99) + \vec{c}}{3} \]

この式を3倍して、

\[ \begin{align*} 3 \times (100, 100) &= (1, 1) + (99, 99) + \vec{c} \\ (300, 300) &= (1, 1) + (99, 99) + \vec{c} \\ (300, 300) &= (100, 100) + \vec{c} \\ \end{align*} \]

$\vec c$を求めると、

\[ \begin{align*}\vec{c} &= (300, 300) – (100, 100) \\ \vec{c} &= (200, 200)\end{align*} \]

点 \( c \) の位置ベクトルは \((200, 200)\) です。