最大公約数と最小公倍数とは?関係式と求め方について

1. 最大公約数 (GCD)
1.1. 公約数とは
公約数とは、2つ以上の整数に共通する約数のことを指します。
12と18の公約数を考えてみましょう。
- 12の約数: 1, 2, 3, 4, 6, 12
- 18の約数: 1, 2, 3, 6, 9, 18
12と18に共通する約数は1、2、3、6です。これが公約数です。
1.2. 最大公約数とは
最大公約数は、2つまたはそれ以上の整数の中で、共通する最大の約数を指します。
- 最大公約数・・・GCDとも呼ばれます。英語で、Greatest Common Divisor。
- gcd(a,b)・・・a,bの最大公約数を意味します。
例えば、36と48の最大公約数を求める場合、両方の約数は次のようになります。
- 36の約数:1, 2, 3, 4, 6, 9, 12, 18, 36
- 48の約数:1, 2, 3, 4, 6, 8, 12, 16, 24, 48
これらの中で共通している最大の約数は12です。したがって、36と48の最大公約数は12です。
2. 最小公倍数
2.1. 公倍数とは
公倍数とは、2つ以上の整数に共通する倍数のことを指します。
12と18の公倍数を考えてみましょう。
- 12の倍数: 12, 24, 36, 48, 60, 72, 84, 96, …
- 18の倍数: 18, 36, 54, 72, 90, 108, …
12と18に共通する倍数は36、72、108、…と続きます。これが公倍数です。
2.2. 最小公倍数 (lcm)
最小公倍数は、2つまたはそれ以上の整数の中で、共通する最小の倍数を指します。
- 最小公倍数・・・LCMとも呼ばれます。英語で、least common multiple。
- lcm(a,b)・・・a,bの最小公倍数を意味します。
例えば、36と48の最小公倍数を求める場合、両方の数の倍数を確認します。
- 36の倍数:36, 72, 108, 144, 180, …
- 48の倍数:48, 96, 144, 192, …
共通する最小の倍数は144です。したがって、36と48の最小公倍数は144です。
3. 最大公約数と最小公倍数の性質
3.1. 最大公約数と最小公倍数の関係式1
\[ \text{gcd}(a, b) \times \text{lcm}(a, b) = a \times b \]
自然数 \(a\) と \(b\) を素因数分解してみましょう。
\(a\) を次のように表します。
\[ a = p_1^{e_1} \times p_2^{e_2} \times \cdots \times p_k^{e_k} \]
\(b\) を次のように表します。
\[ b = p_1^{f_1} \times p_2^{f_2} \times \cdots \times p_k^{f_k} \]
ここで、\(p_1, p_2, \dots, p_k\) は素数、\(e_i\) と \(f_i\) はそれぞれの指数です。もしある素数 \(p_i\) が片方にしか含まれない場合、その指数は0として考えます。
\(a\) と \(b\) の最大公約数は、それぞれの素因数の最小の指数で表されます。すなわち、次の式で表されます。
\[ \text{gcd}(a, b) = p_1^{\min(e_1, f_1)} \times p_2^{\min(e_2, f_2)} \times \cdots \times p_k^{\min(e_k, f_k)} \]
ここで、$min(e_i,f_i)$は$e_i$と$f_i$のどちらかの小さい値を選択する関数です。
同様に、最小公倍数は、それぞれの素因数の最大の指数で表されます。すなわち、次の式で表されます。
\[ \text{lcm}(a, b) = p_1^{\max(e_1, f_1)} \times p_2^{\max(e_2, f_2)} \times \cdots \times p_k^{\max(e_k, f_k)} \]
ここで、$max(e_i,f_i)$は$e_i$と$f_i$のどちらかの大きい値を選択する関数です。
\( \text{gcd}(a, b) \times \text{lcm}(a, b) \) の計算をしてみます。
\[ \text{gcd}(a, b) \times \text{lcm}(a, b) = \left( p_1^{\min(e_1, f_1)} \times p_2^{\min(e_2, f_2)} \times \cdots \times p_k^{\min(e_k, f_k)} \right) \times \left( p_1^{\max(e_1, f_1)} \times p_2^{\max(e_2, f_2)} \times \cdots \times p_k^{\max(e_k, f_k)} \right) \]
これは、素因数ごとに次のように計算できます。
\[ p_1^{\min(e_1, f_1) + \max(e_1, f_1)} \times p_2^{\min(e_2, f_2) + \max(e_2, f_2)} \times \cdots \times p_k^{\min(e_k, f_k) + \max(e_k, f_k)} \]
ここで、次の性質を利用します。
\[ \min(e_i, f_i) + \max(e_i, f_i) = e_i + f_i \]
この式の意味は単に、2つの値のうち小さい方と大きい方 をそれぞれ選んで足すと、結局その2つの元の値を足した結果と同じになる、ということです。
したがって、上記の式は次のようになります。
\[ p_1^{e_1 + f_1} \times p_2^{e_2 + f_2} \times \cdots \times p_k^{e_k + f_k} \]
これは、 \(a \times b\) を素因数分解した形です。したがって、次の関係が成り立ちます。
\[ \text{gcd}(a, b) \times \text{lcm}(a, b) = a \times b \]
例えば、36と48の場合、次のように確認できます。
\[ 12 \times 144 = 36 \times 48 \]
この関係は常に成り立ちます。
3.2. 最大公約数と最小公倍数の関係式2
\[ \text{lcm}(a, b) = \text{gcd}(a, b) \times a’ \times b’ \]
ここで、$a’$と$b’ $は互いに素である。
最大公約数と最小公倍数には、先ほど示したように、次の関係式が成り立ちます。
\[ \text{lcm}(a, b) \times \text{gcd}(a, b) = a \times b \]
この関係を用いることで、次のように式を変形できます。
\[\begin{align*} \frac{\text{lcm}(a, b) \times \text{gcd}(a, b)}{\text{gcd}(a, b)}& = \frac{a \times b}{\text{gcd}(a, b)} \\ &=\frac{a \times b}{\text{gcd}(a, b)} \\ &=\text{gcd}(a, b)\frac{a \times b}{\text{gcd}(a, b)\times \text{gcd}(a, b)} \end{align*}\]
ここで、\( a’ = \frac{a}{\text{gcd}(a,b)} \) および \( b’ = \frac{b}{\text{gcd}(a,b)} \) ですから、
\[ \text{lcm}(a, b) = \text{gcd}(a, b) \times a’ \times b’ \]
4. 例題
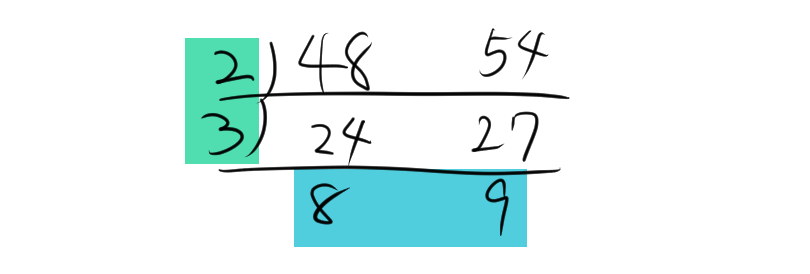
次の図のように、まずは公約数で割っていきます。青色で示された部分は、数値同士が互いに素(公約数が1しかない状態)になるまで割り続けます。そして、これ以上公約数で割ることができなくなった段階で、緑色の部分に残った積が最大公約数となります。一方で、この緑色の部分にある積が最大公約数であることに加えて、青色の互いに素である部分の積と掛け合わせると、
$$\text{lcm}(a, b) = \text{gcd}(a, b) \times a’ \times b’$$
になるので、最小公倍数になります。したがって、
$最大公約数=6$
$最小公倍数=6\times 72 = 432$