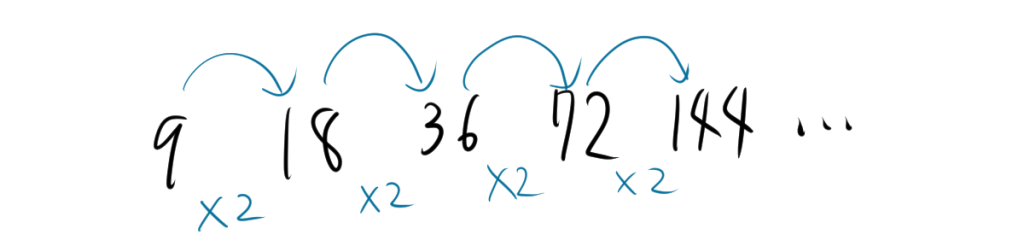等比数列とは?例題や定義、性質、漸化式について

1. 等比数列
等比数列とは、隣り合う項の比が常に一定である数列のことです。この一定の比を公比と呼びます。
\[ a_n = a_1 \cdot r^{n-1} \]
ここで、
- \(a_n\) は第 \(n\) 項、
- \(a_1\) は初項、
- \(r\) は公比、
- \(n\) は項数です。
等比数列は幾何数列とも呼ばれます。
1.1. 等比数列の例
例えば、初項が 2、公比が 3 の等比数列は次のようになります。
\[ 2, 6, 18, 54, 162, \dots \]
この数列では、各項が前の項の 3 倍になっています。
1.2. 等比数列の漸化式
等比数列において、次の項は常に前の項に一定の数(公比 \( r \))を掛けたものになります。初項 \( a_1 \)、公比 \( r \) の等比数列 \( a_1, a_2, a_3, \dots \) に対して、漸化式は次のように表されます。
\[ a_{n+1} = r \cdot a_n \]
ここで、
- \( a_n \) は第 \( n \) 項、
- \( r \) は公比、
- \( a_1 \) は初項です。
例えば、初項 \( a_1 = 2 \) で、公比 \( r = 3 \) の場合、漸化式は次のようになります。
\[ a_{n+1} = 3 \cdot a_n \]
2. 例題
- 一般項 \( a_n \) を求めなさい。
- この等比数列の漸化式を立てなさい。
- 第5項 \( a_5 \) の値を求めなさい。
初項 \( a_1 = 3 \) と公比 \( r = 2 \) であるから、
\[ a_n = 3 \cdot 2^{n-1} \]
等比数列は、前項に公比を掛けることで次項が得られるため、漸化式は以下のようになります。
\[ a_{n+1} = 2 \cdot a_n \]
一般項の式に \( n = 5 \) を代入して求めます。
\[ a_5 = 3 \cdot 2^{5-1} = 3 \cdot 2^4 = 3 \cdot 16 = 48 \]
よって、第5項は \( a_5 = 48 \) です。
3. 等比数列の性質
3.1. 任意の項の比が一定
\[ \frac{a_{n+1}}{a_n} = r \]
3.2. 項の積の性質
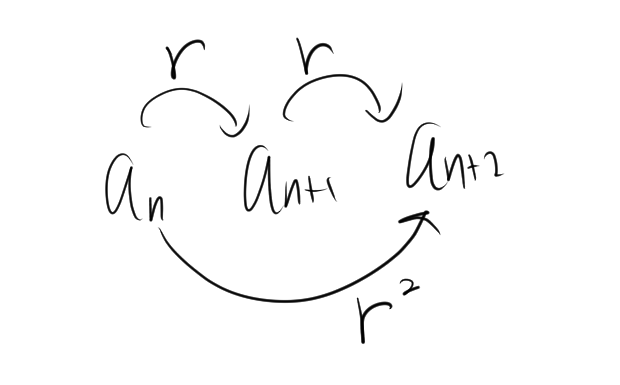
\[ a_{n+1}^2 = a_n \cdot a_{n+2} \]
$a_{n+1}$を2乗すると、
$$a_{n+1}^2 = r ^2\cdot a_n^2$$
ここで、$r^2a_n=a_{n+2}$であるから、
$$a_{n+1}^2 = a_na_{n+2}$$
この関係を図にすると、
3.3. 和の公式
- 公比 \( r \neq 1 \) の場合:
\[ S_n = a_1 \cdot \frac{1 – r^n}{1 – r} \]
- 公比 \( r = 1 \) の場合:
\[ S_n = a_1 \cdot n \]
3.4. 無限等比数列の和
\[ S = \frac{a_1}{1 – r} \]
3.5. 対数と等差数列
$a_n = a \cdot r^{n-1}$のとき、対数をとると、
$$\log a_n = \log a +(n-1) \log r$$
となるので、これは等差数列の一般項である。ただし、対数をとるために、$a_n \geq 0,a \geq 0,r \geq 0$である必要がある。