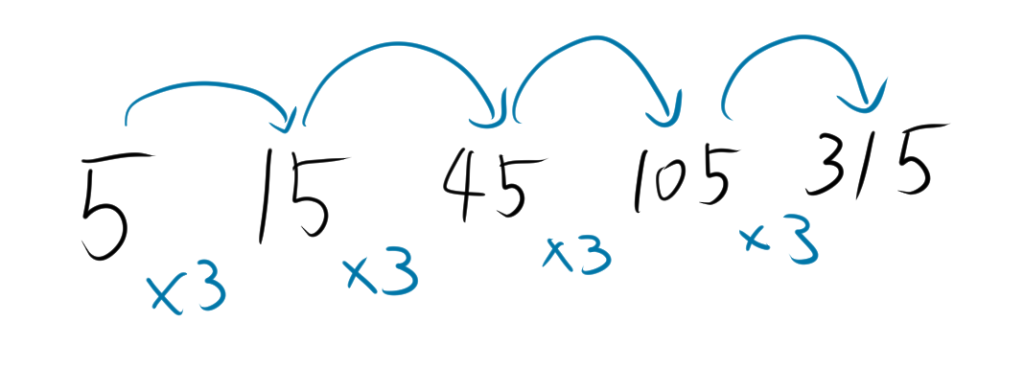等比数列の和の公式の証明、例題について

1. 等比数列とは

等比数列とは、隣り合う項の比が一定である数列を指します。この一定の比を公比（\(r\)）と呼び、初項を \(a\) とします。

2. 等比数列の和

3. 等比数列の和の証明

3.1. 証明1：差を計算

公比（\(r\)）、初項を \(a\) とした等比数列の初項から第 \(n\) 項までの和 \(S_n\) を考えます。この和は次のような式で求められます。

\[ S_n = a + a r + a r^2 + \cdots + a r^{n-1} \]

まず、和の両辺に \(r\) をかけます。

\[ r S_n = a r + a r^2 + a r^3 + \cdots + a r^n \]

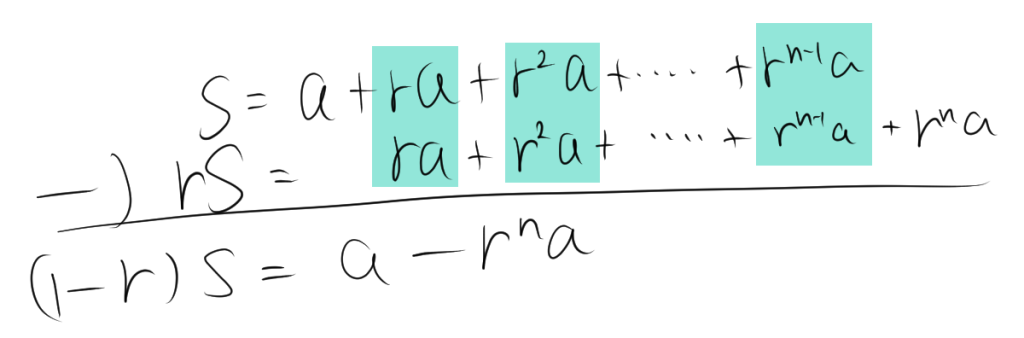
元の式$S_n$と$rS_n$の引き算をすると、

\[ S_n – r S_n = a – a r^n \]

これを整理すると、

\[ S_n (1 – r) = a (1 – r^n) \]

従って、\(r \neq 1\) の場合、等比数列の和は次の式で与えられます。

\[ S_n = \frac{a (1 – r^n)}{1 – r} \]

もし \(r = 1\) であれば、この場合はすべての項が同じ値になりますので、単純に次のようになります。

\[ S_n = a \cdot n \]

---

計算のイメージは

3.2. 証明2：数学的帰納法

数学的帰納法を利用して証明します。

---

まず、\(n = 1\) のとき、公式が成り立つか確認します。

等比数列の和の公式は次の通りです。

\[ S_1 = a \]

一方、公式 \(\frac{a(1 – r^n)}{1 – r}\) を \(n = 1\) に適用すると

\[ S_1 = \frac{a(1 – r^1)}{1 – r} = \frac{a(1 – r)}{1 – r} = a \]

よって、初項の場合、公式は成り立っています。

次に、ある \(n = k\) の場合に公式が成り立つと仮定します。この仮定を数学的帰納法の仮定とします。つまり、

\[ S_k = \frac{a(1 – r^k)}{1 – r} \]

が成り立っていると仮定します。

\(n = k + 1\) の場合の和 \(S_{k+1}\) を表します

\[ S_{k+1} = S_k + a r^k \]

ここで、仮定より、

\[ \begin{align*} S_{k+1} &= \frac{a(1 – r^k)}{1 – r} + a r^k \\ & = \frac{a(1 – r^k) + a r^k (1 – r)}{1 – r} \\ &= \frac{a(1 – r^k + r^k – r^{k+1})}{1 – r} \end{align*}\]

つまり、

\[ S_{k+1} = \frac{a(1 – r^{k+1})}{1 – r} \]

これで、\(n = k + 1\) の場合にも公式が成り立つことが証明されました。数学的帰納法により、等比数列の和の公式、

\[ S_n = \frac{a(1 – r^n)}{1 – r} \]

がすべての \(n \geq 1\) に対して成り立つことが示されました。

4. 等比数列の問題

4.1. 問題 1

この等比数列の一般項は、

\[ a_n = 3 \cdot 2^{n-1} \]

したがって、第6項までの和 \( S_6 \) は、

\[ S_6 = 3 \cdot \frac{2^6 – 1}{2 – 1} = 3 \cdot (64 – 1) = 3 \cdot 63 = 189 \]

第6項までの和は 189 です。

4.2. 問題 2

この数列は公比 \( r = -\frac{2}{7} \) の等比数列であるので、

\[ S_4 = 7 \times \frac{1 – \left(-\frac{2}{7}\right)^4}{1 – \left(-\frac{2}{7}\right)} \]

まずは \( \left(-\frac{2}{7}\right)^4 = \frac{16}{2401} \) を計算し、続けて和を計算します。

\[\begin{align*} S_4 &= 7 \times \frac{1 – \frac{2^4}{7^4}}{1 + \frac{2}{7}} \\ &= 7 \times \frac{\frac{7^4-2^4}{7^4}}{\frac{9}{7}} \\ &=7 \times\frac{7^4-2^4}{7^4} \times \frac{7}{9} \\ &=\frac{(7^2+2^2)(7^2-2^2)}{9\cdot 7^2}\\ &=\frac{51\cdot 45}{9\cdot 7^2}\\ &=\frac{51\cdot 5}{ 7^2}\\ &= \frac{265}{49} \end{align*}\]

したがって、数列の4項の和は \( \frac{265}{49} \) です。