はるか
今日は勾配について話そう。
ふゅか
そうね！勾配はベクトル解析やディープラーニングでよく使われる重要な概念よ。楽しみだね♪
勾配とは
勾配は、多変数関数に対する各変数の偏微分を成分とするベクトルです。具体的には、スカラー値関数 \( f \) の勾配（gradient）は次のように定義されます：
\[ \mathrm{grad} f = \nabla f = \left( \frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, \ldots, \frac{\partial f}{\partial x_n} \right) \]
ここで、\( f \) は \( n \) 個の変数 \( x_1, x_2, \ldots, x_n \) を持つ多変数関数です。
勾配の特徴
勾配の主な特徴は次の通りです。
- 方向：勾配ベクトルは、関数 \( f \) の値が最も急速に増加する方向を示します。逆に、マイナスの勾配ベクトルは、関数の値が最も急速に減少する方向を示します。
- 大きさ：勾配ベクトルの大きさ（ノルム）は、その方向に沿った増加の速度を示します。ノルムが大きいほど、関数の値はその方向に急速に変化します。
勾配の計算の具体例
ふゅか
実際の計算例を見てみよう！例えば、2変数関数 $f(x,y)=x^2+y$ の勾配はどうなるのかな？
はるか
偏微分を計算する。
2変数関数 \( f(x,y) = x^2 + y \) の勾配は、関数の各変数に関する偏微分を計算することで求められます。勾配ベクトルは次のように定義されます。
\[ \nabla f(x,y) = \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right) \]
この関数について偏微分を計算します。
- \( x \) に関する偏微分： \[ \frac{\partial f}{\partial x} = \frac{\partial}{\partial x}(x^2 + y) = 2x \]
- \( y \) に関する偏微分： \[ \frac{\partial f}{\partial y} = \frac{\partial}{\partial y}(x^2 + y) = 1 \]
したがって、関数 \( f(x,y) = x^2 + y \) の勾配ベクトルは次のようになります。
\[ \nabla f(x,y) = (2x, 1) \]
勾配を可視化したグラフ
ふゅか
せっかくなので、勾配を可視化してみましょう！
可視化したグラフ1
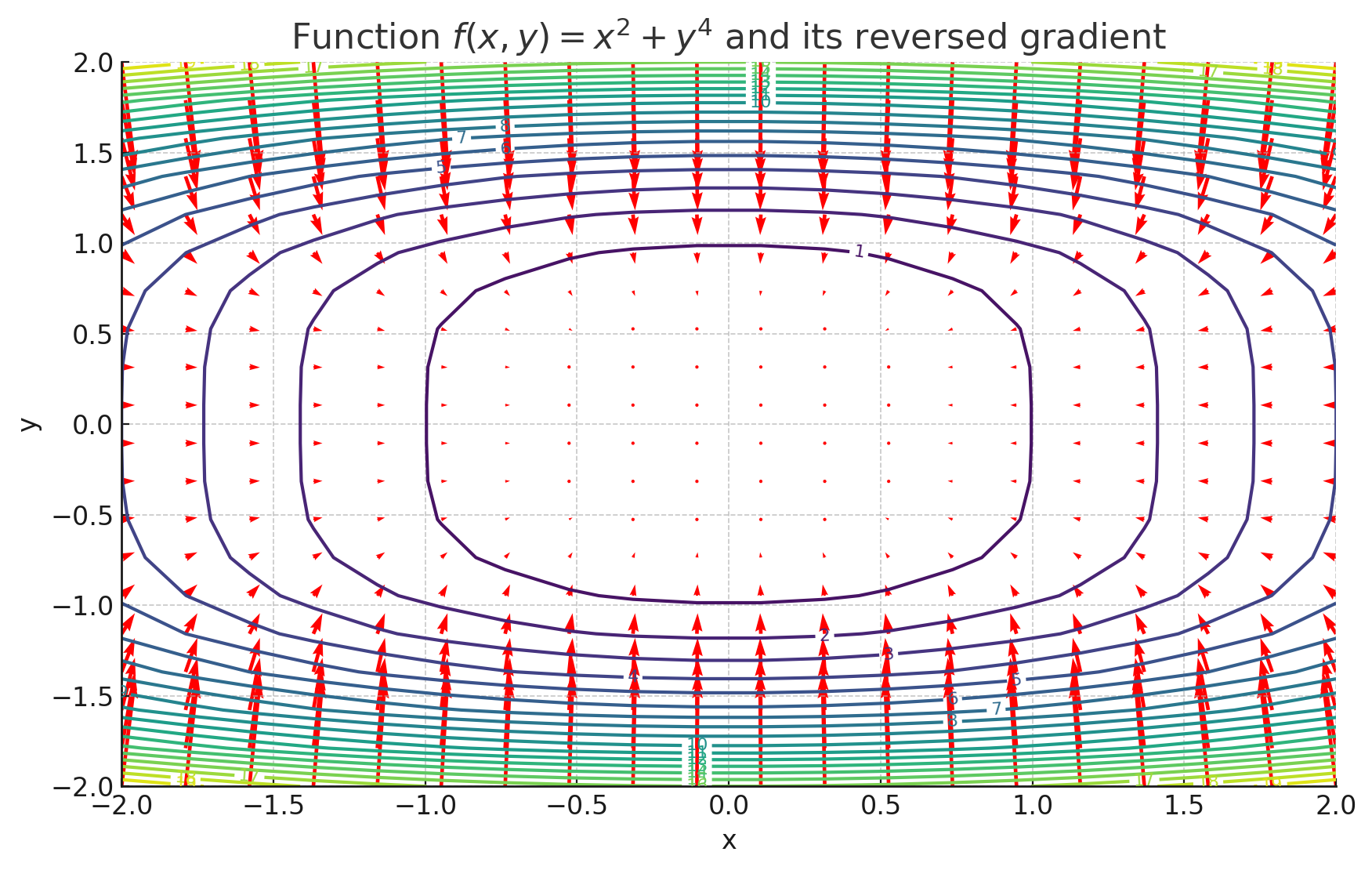
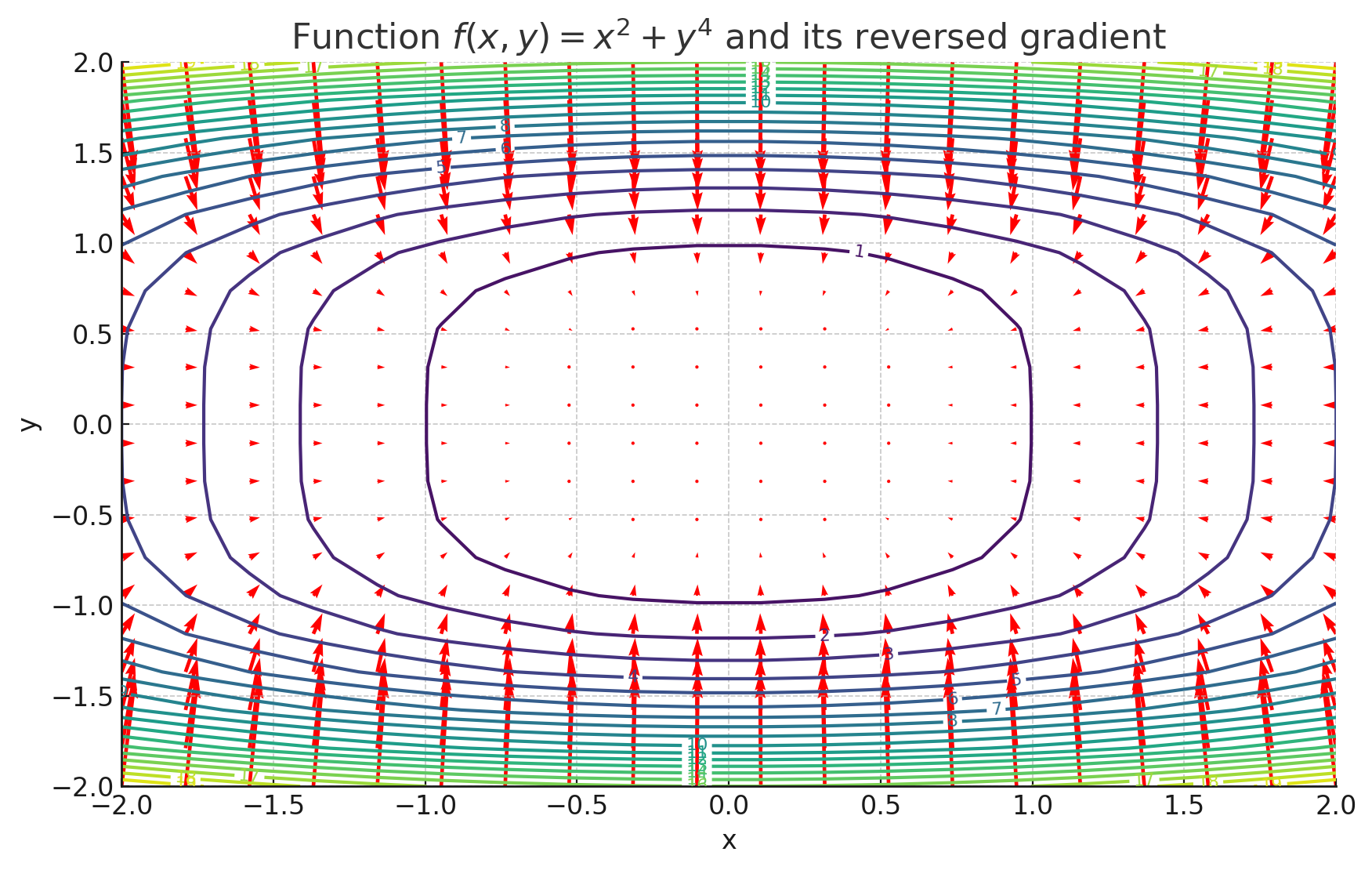
$x^2+y^4$の等高線と逆向きにした勾配ベクトルを表示したグラフです。赤い矢印が各点における逆向きの勾配ベクトルを示しており、各点における関数が最も急速に減少する方向を示しています。最小値をとる(0,0)を指しているように見えます。
はるか
各点で関数が最も急速に減少する方向。
可視化したグラフ2
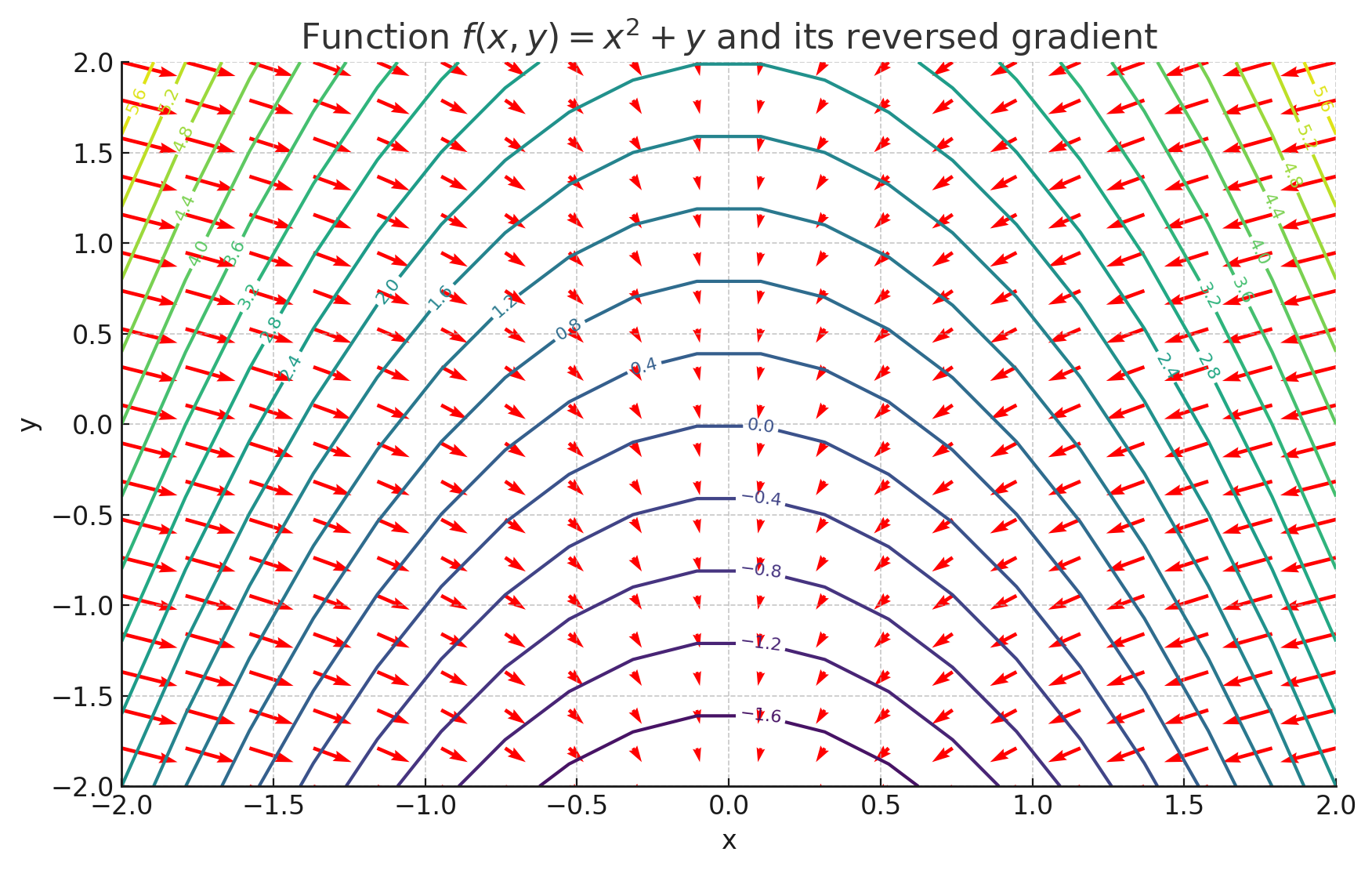
$x^2+y$の等高線と逆向きにした勾配ベクトルを表示したグラフです。赤い矢印が各点における逆向きの勾配ベクトルを示しており、各点における関数が最も急速に減少する方向を示しています。
ふゅか
関数の変化を視覚的に確認できました！