更新:2024/07/25
勾配法について!関数の最小値をpythonで求める
はるか
勾配法は、損失関数の最適化で使われる方法の一つ。
ふゅか
そうね!関数の最小値も見つけることができる!
目次
1. 勾配法の手順
勾配法を用いて、関数の最小値を見つけるための手順を示します。
- 初期値 \((x_0, y_0)\) を設定します。
- 学習率 \(\alpha\) を設定します。
- 以下の更新式を用いて、変数を更新します。2変数関数の場合は次のようになります。
\[ x_{n+1} = x_n – \alpha \frac{\partial f}{\partial x} (x_n, y_n) \]\[ y_{n+1} = y_n – \alpha \frac{\partial f}{\partial y} (x_n, y_n) \]
ふゅか
まずは初期値を設定するよね。そして、学習率を決めるの。これで、どれくらいの大きさで次のステップに進むかが決まるんだ。
はるか
更新式で、各地点における、関数の値が最も急速に減少する方向について徐々に移動。
2. 勾配法を用いて最小値を求める
$(1,1)$から$z=x^2+y^4$の最小値を勾配法で求めます。
2.1. 勾配の計算
関数 \( f(x, y) = x^2 + y^4 \) の最小値を勾配法で求めるために、まず勾配を計算します。勾配とは、各変数に関する偏微分をベクトルにしたものです。以下にその手順を示します。
\[ \nabla f(x, y) = \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right) \]
各偏微分を計算します。
\[
\frac{\partial f}{\partial x} = 2x
\]
\[
\frac{\partial f}{\partial y} = 4y^3
\]
したがって、勾配は以下のようになります。
\[
\nabla f(x, y) = (2x, 4y^3)
\]
この勾配をもとにプログラムを実行すると、関数 \( f(x, y) = x^2 + y^4 \) の最小値を求めることができます。繰り返し回数や学習率を調整することで、より正確な結果を得ることができます。この関数の最小値は \((0, 0)\) であり、その値は 0 です。
2.2. 勾配法のpythonプログラム
ふゅか
Pythonを使って実際に勾配法を実装してみよう!初期値や学習率を設定して、変数を更新するプログラムを書くんだ。
はるか
プログラムの実行結果を確認。
import matplotlib.pyplot as plt
def gradient_descent(initial_x, initial_y, learning_rate, num_iterations):
x, y = initial_x, initial_y
path_x, path_y = [x], [y]
for _ in range(num_iterations):
grad_x = 2 * x
grad_y = 4 * y ** 3
x = x - learning_rate * grad_x
y = y - learning_rate * grad_y
path_x.append(x)
path_y.append(y)
return x, y, path_x, path_y
initial_x, initial_y = 1, 1
learning_rate = 0.001
num_iterations = 1000
min_x, min_y, path_x, path_y = gradient_descent(initial_x, initial_y, learning_rate, num_iterations)
min_value = min_x ** 2 + min_y ** 4
print(f"最小値の座標: ({min_x}, {min_y})")
print(f"最小値: {min_value}")
plt.figure(figsize=(10, 6))
plt.plot(path_x, path_y, 'bo-', markersize=3, linewidth=1)
plt.scatter([initial_x], [initial_y], color='red', label='Initial Point')
plt.scatter([min_x], [min_y], color='green', label='Minimum Point')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Gradient Descent Path')
plt.legend()
plt.grid(True)
plt.show()はるか
学習率を変えることで、収束のスピードや精度が変わる。
ふゅか
学習率を変えて確認してみよう!
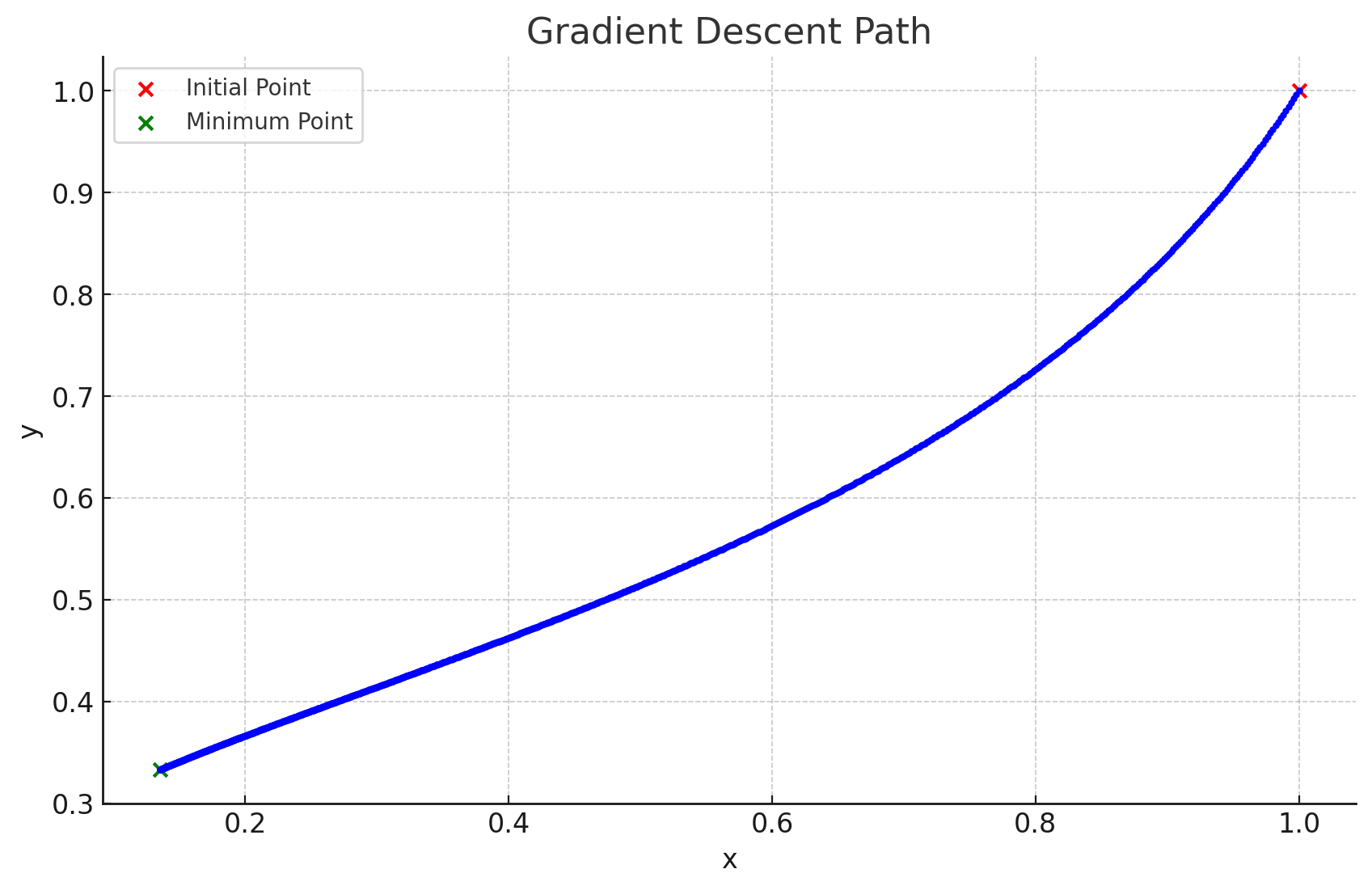
2.3. 学習率を0.001にしたとき
learning_rateを0.001にした時の、グラフは次のようになります。
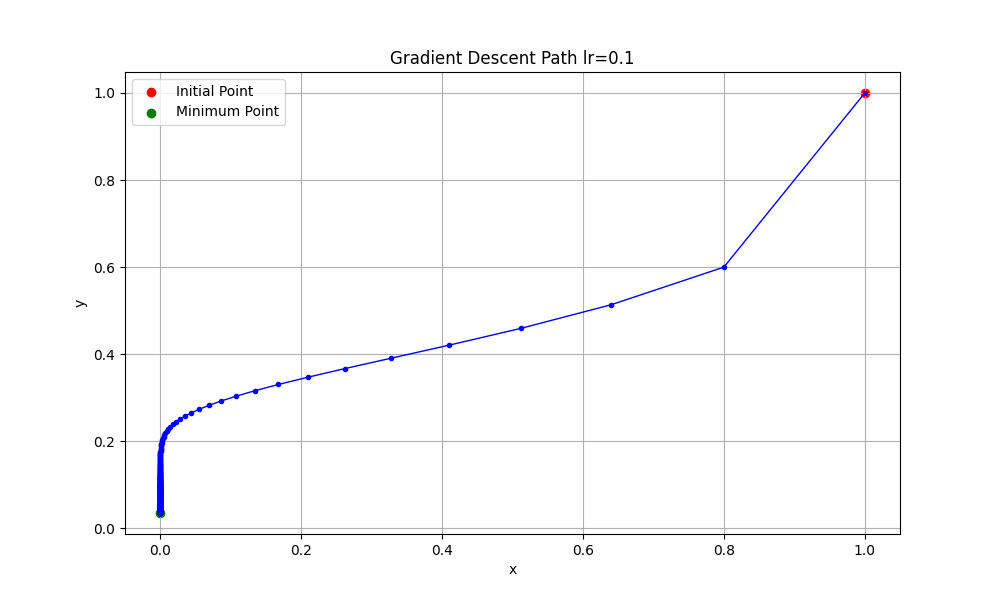
2.4. 学習率を0.1にしたとき
learning_rateを0.1にした時の、グラフは次のようになります。
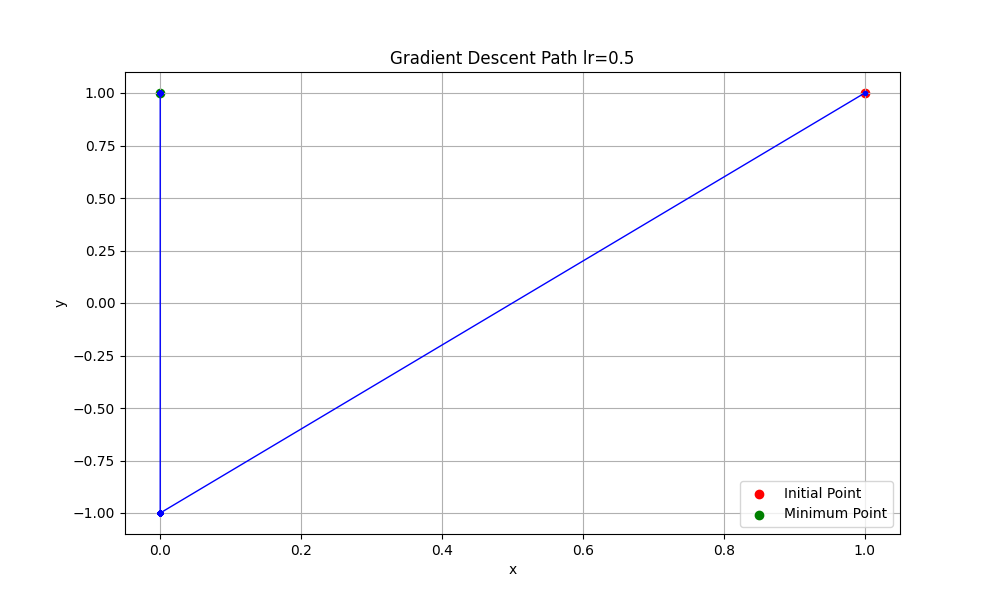
2.5. 学習率を0.5にしたとき
learning_rateを0.5にした時の、グラフは次のようになります。
PR