グラムシュミットの直交化法の定義・例題・計算方法

1. グラムシュミットの直交化法でできること

与えられた線形独立のベクトルを、それぞれが互いに直交するように変換することができます。例えば、線形独立なベクトル$a_{1}$と$a_{2}$が与えられているときに、$a_{1}$と$a_{2}$を用いて、正規直交基底$u_{1}$、$u_{2}$を表すことができる。

2. グラムシュミットの直交化法の方法

以下のステップを踏むことで、グラムシュミットの直交化法を行うことができます。

2.1. step1:正規化

$$\boldsymbol{u}_{1} = \dfrac{\boldsymbol{a}_{1}}{|| \boldsymbol{a}_{1}||}$$

$\boldsymbol{a}_{1}$を長さ1の単位ベクトル$\boldsymbol{u}_{1}$に正規化している。

2.2. step2:成分の除去

$$\boldsymbol{u}_{2}^{‘}=\boldsymbol{a}_{2}-(\boldsymbol{a}_{2} \cdot \boldsymbol{u}_{1})\boldsymbol{u}_{1}$$

として、$a_{2}$に含まれている、$u_{1}$の成分を除去する。

$$\boldsymbol{u}_{2}=\dfrac{\boldsymbol{u}_{2}^{‘}}{||\boldsymbol{u}_{2}^{‘}||}$$

$\boldsymbol{u}_{2}^{‘}$を長さ1の単位ベクトル$\boldsymbol{u}_{2}$に正規化している。

2.3. step3:ステップ2の繰り返し

$2$~$n$まで以下の操作を行う。step2は$n=2$の時の例である。

$$\boldsymbol{u}^{‘}_{n}=\boldsymbol{a}_{n}-\displaystyle\sum^{n-1}_{i=1}(\boldsymbol{a}_{n} \cdot \boldsymbol{u}_{i})\boldsymbol{u}_{i}$$

$\boldsymbol{a}_{n}$から$\boldsymbol{u}_{1}$、$\boldsymbol{u}_{2}$・・・・、$\boldsymbol{u}_{n-1}$の成分を除去する。

$$\boldsymbol{u}_{n}=\dfrac{\boldsymbol{u}_{n}^{‘}}{||\boldsymbol{u}_{n}^{‘}||}$$

$\boldsymbol{u}_{n}^{‘}$を長さ1の単位ベクトル$\boldsymbol{u}_{n}$に正規化している。

3. 直交していることを確認する

グラムシュミットの直交化法を利用して生成したベクトルが実際に直交しているのか、$\boldsymbol{u}^{‘}_{n}$と$\boldsymbol{u}_{i}$が直交するのか確認する。ただし、iは$1 \leq i \leq n-1$を満たす自然数とする。$i \neq j$のとき　正規直交基底の内積は$u_{i} \cdot u_{j}=0$、$||u_{i}||^2=1$ となるため、

$$\boldsymbol{u}^{‘}_{n} \cdot \boldsymbol{u}_{i}=\boldsymbol{a}_{n} \cdot \boldsymbol{u}_{i} -\displaystyle\sum^{n-1}_{k=1}(\boldsymbol{a}_{n} \cdot \boldsymbol{u}_{i})\boldsymbol{u}_{k} \cdot \boldsymbol{u}_{i}$$

$$=\boldsymbol{a}_{n} \cdot \boldsymbol{u}_{i} -(\boldsymbol{a}_{n}\cdot \boldsymbol{u}_{i}) \boldsymbol{u}_{i}\cdot \boldsymbol{u}_{i}$$

$$=\boldsymbol{a}_{n} \cdot \boldsymbol{u}_{i} -(\boldsymbol{a}_{n}\cdot \boldsymbol{u}_{i}) ||\boldsymbol{u}_{i}||^2$$

$$=\boldsymbol{a}_{n} \cdot \boldsymbol{u}_{i} -\boldsymbol{a}_{n}\cdot \boldsymbol{u}_{i}$$

$$=0$$

となるため、直交している。

4. グラムシュミットの直交化法の例題

まず、$\boldsymbol{u}_{1}$を求める。$||\boldsymbol{a}||=\sqrt{3}$であるから、

$\boldsymbol{u}_{1}=\dfrac{\boldsymbol{a}_{1}}{\sqrt{3}}$

$=\dfrac{1}{\sqrt{3}}\begin{bmatrix} 1 \\ 1 \\ 1 \\ \end{bmatrix}$

次に$\boldsymbol{u}^{‘}_{2}$を求める。

$\boldsymbol{u}_{2}^{‘}=\boldsymbol{a}_{2}-(\boldsymbol{a}_{2} \cdot \boldsymbol{u}_{1})\boldsymbol{u}_{1}$

$=\begin{bmatrix} 1 \\ 0 \\ 0 \\ \end{bmatrix}-\dfrac{1}{\sqrt{3}}\boldsymbol{u}_{1}$

$=\begin{bmatrix} 1 \\ 0 \\ 0 \\ \end{bmatrix}-\dfrac{1}{3}\begin{bmatrix} 1 \\ 1 \\ 1 \\ \end{bmatrix}$

$=\dfrac{1}{\sqrt{3}}\begin{bmatrix} 2 \\ -1 \\ -1 \\ \end{bmatrix}$

$\boldsymbol{u}^{‘}_{2}$ベクトルを正規化すると、

$\boldsymbol{u}_{2}=\dfrac{1}{\sqrt{6}}\begin{bmatrix} 2 \\ -1 \\ -1 \\ \end{bmatrix}$

次に$\boldsymbol{u}^{‘}_{3}$を求める。

$\boldsymbol{u}_{3}^{‘}=\boldsymbol{a}_{3}-(\boldsymbol{a}_{3} \cdot \boldsymbol{u}_{1})\boldsymbol{u}_{1}-(\boldsymbol{a}_{3} \cdot \boldsymbol{u}_{2})\boldsymbol{u}_{2}$

$=\boldsymbol{a}_{3}-\dfrac{1}{\sqrt{3}}\boldsymbol{u}_{1}+\dfrac{1}{\sqrt{6}}\boldsymbol{u}_{2}$

$=\begin{bmatrix} 0 \\ 1 \\ 0 \\ \end{bmatrix}-\dfrac{1}{3}\begin{bmatrix} 1 \\ 1 \\ 1 \\ \end{bmatrix}+\dfrac{1}{6}\begin{bmatrix} 2 \\ -1 \\ -1 \\ \end{bmatrix}$

$=\dfrac{1}{2}\begin{bmatrix} 0 \\ 1 \\ -1 \\ \end{bmatrix}$
$\boldsymbol{u}^{‘}_{3}$ベクトルを正規化すると、
$\boldsymbol{u}_{3}=\dfrac{1}{\sqrt{2}}\begin{bmatrix} 0 \\ 1 \\ -1 \\ \end{bmatrix}$

4.1. 求めた正規直交基底を可視化する

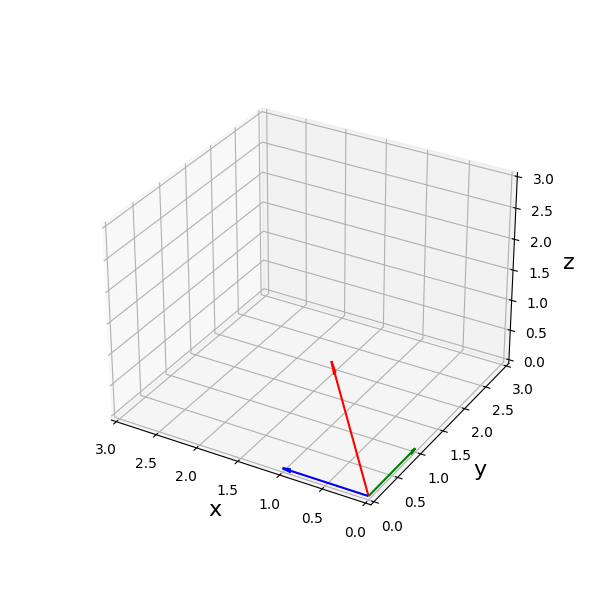
$\boldsymbol{a}_{1}$が赤色、$\boldsymbol{a}_{2}$が青色、$\boldsymbol{a}_{3}$が緑色で表示されています。

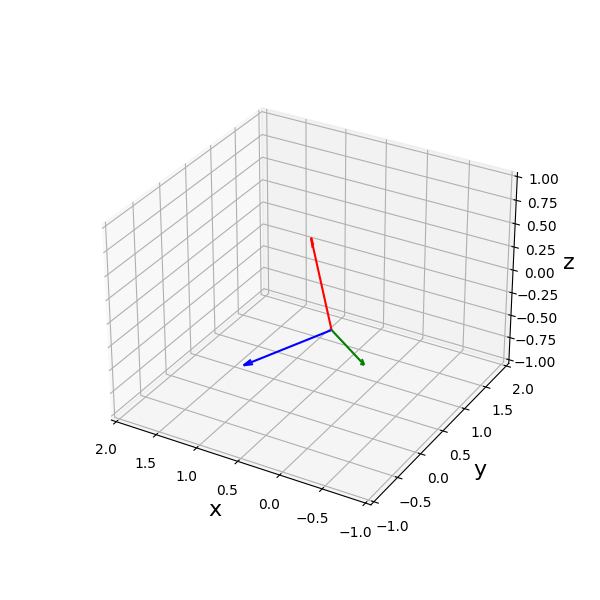
$u_{1}$が赤色、$u_{2}$が青色、$u_{3}$が緑色で表示されています。

4.2. 検算方法

正規直交基底であるから、内積が0でベクトルの大きさが１であればよいため、例えば、

$(u_1,u_2)=0$

$||u_1||=1$

となるかどうかを計算すればよい。